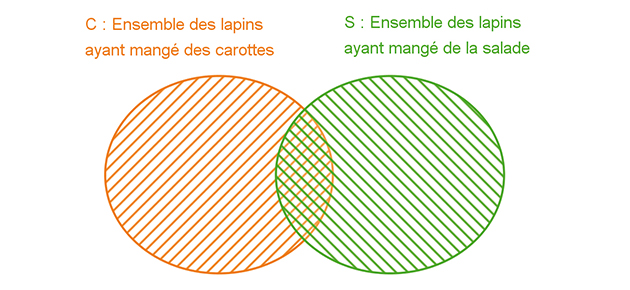
Lors du dernier repas de la famille Lapinou, 80% des individus ont mangé des carottes, 45% ont mangé de la salade et 30% ont mangé des deux. Quelle est la proportion des individus ayant mangé des carottes ou de la salade (c'est-à-dire au moins un des deux aliments) ?

Pour répondre, un petit dessin vaut mieux qu'un long discours. Il suffit de regarder l'image ci-dessous dans laquelle on a représenté l'ensemble C des lapins ayant mangé des carottes et l'ensemble S de ceux ayant mangé de la salade. Si l'on additionne les deux proportions respectives, on s'aperçoit sur le dessin qu'on a compté une fois de trop les lapins qui se trouvent à l'intersection des deux ensembles, c'est-à-dire ceux qui ont mangé des carottes et de la salade. Ainsi, la proportion cherchée est égale à 80% + 45% – 30% = 95%. En notant p_C et p_S les proportions des ensembles C et S, on peut même en tirer une formule plus générale :

\( p_{C\cup S}=p_C+p_S-p_{C\cap S}.\)

Les petits dessins de ce genre étaient déjà utilisés par Leonhard Euler au XVIII^e siècle dans un contexte légèrement différent puisqu'il concernait l'illustration d'expressions logiques.

En quête d'esthétique

Un siècle plus tard, le mathématicien britannique John Venn (1834-1923) s'intéresse de plus près à ces diagrammes et envisage de les généraliser à un nombre quelconque de sous-ensembles dans un article publié en 1880 dans le Philosophical Magazine and Journal of Science et intitulé On the Diagrammatic and Mechanical Representation of Propositions and Reasonings.

Pour trois sous-ensembles, tout se passe plutôt bien. L'examen attentif du dessin obtenu permet d'ailleurs d'établir une jolie formule sur les proportions :

\( p_{A\cup B\cup C}=p_A+p_B+p_C-p_{A\cap C}-p_{B\cap C}-p_{A\cap B \cap C}\)

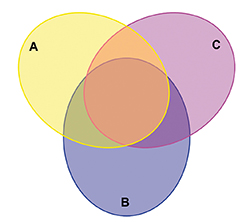Si l'on augmente le nombre de sous-ensembles, l'idée est bien tentante de voir à quoi peuvent ressembler les diagrammes de Venn, ainsi appelés depuis la publication en 1918 de A Survey of Symbolic Logic du philosophe et logicien américain Clarence Irving Lewis (1883-1964). Mais que désigne un diagramme de Venn exactement ? Son but est de représenter chaque sous-ensemble par des courbes fermées simples (des « patates »), de telle sorte qu'elles délimitent autant de régions (d'un seul tenant) que d'intersections envisageables. Pour n sous-ensembles, il faut obtenir 2ⁿ régions (l'extérieur compte pour une région).

Pour quatre sous-ensembles, on peut repartir du diagramme obtenu pour trois sous-ensembles et « serpenter » autour des régions précédentes pour dessiner le quatrième.

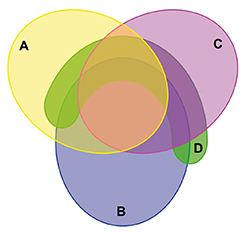Hélas, de l'aveu de John Venn lui-même, la figure n'est pas des plus lisibles. On peut continuer ainsi pour cinq, six, sept sous-ensembles et plus, en serpentant autour du dernier ensemble tracé, mais la clarté du diagramme ne devient alors plus qu'un lointain souvenir.

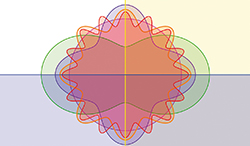
La lisibilité des diagrammes de Venn est une question… difficile. Déjà, à quelles conditions un tel diagramme est-il effectivement lisible ? Les images symétriques sont souvent synonymes de clarté et les formes utilisées doivent être élémentaires. Ce qui commence à poser problème dans le diagramme à quatre sous-ensembles, c'est la forme alambiquée de la partie D, qui n'est plus identique aux autres. L'image idéale serait constituée de n ellipses et resterait identique par une rotation (d'angle 2π/n radians). Pour n = 5, on obtient une image plutôt limpide compte tenu de la complexité de la situation et des trente-deux cas différents à représenter.

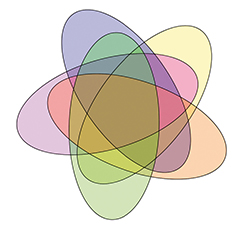
  ^{Un diagramme de Venn symétrique à cinq ellipses.}

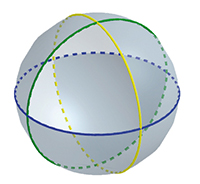
 Certains cas semblent bien difficiles à traiter, même pour de petites valeurs de n. En 1989, le biologiste britannique Anthony Edwards développe une autre méthode : pourquoi ne pas dessiner nos patates sur une sphère ? Il suffirait ensuite de projeter le résultat obtenu sur le plan. Considérons par exemple le cas n = 3. Il est ramené à trois hémisphères se coupant deux à deux, comme sur le schéma ci-dessous.

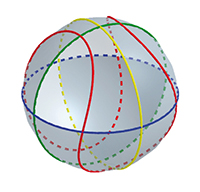
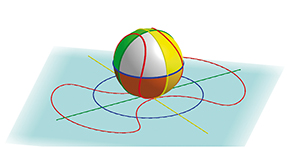
Pour ajouter un quatrième sous-ensemble, on peut suivre la ligne dessinée sur une balle de tennis qui serpente d'une région à une autre sur toute la surface de la sphère. En augmentant ainsi le nombre d'ondulations, on peut représenter de façon élégante un diagramme de Venn pour n'importe quelle valeur de n.

Tennis et cacahuètes

Les diagrammes d'Edwards-Venn sont une traduction dans le plan de ce procédé mis en œuvre sur la sphère. On commence par dessiner une droite horizontale, ce qui délimite un ensemble. On ajoute une deuxième droite, perpendiculaire à la première, pour délimiter un deuxième ensemble ; on obtient alors quatre régions différentes. On ajoute ensuite sur cette figure un cercle ce qui permet bien de délimiter huit régions distinctes. Pour passer à seize régions, on dessine une courbe en forme de cacahuète, celle qui correspond au dessin de la balle de tennis sur la sphère. On obtient ainsi une carte du globe.

Il suffit ensuite de poursuivre en doublant le nombre d'ondulations à chaque étape. Admirez le résultat !