L'existence de l'ensemble vide  \( \emptyset\)  exige que, si l'on veut définir une opération sur des ensembles, on soit obligé de l'envisager. De façon étonnante, cela simplifie la description de l'ensemble des parties d'un ensemble. Déjà, la seule partie de l'ensemble vide est… l'ensemble vide lui-même. L'idée est ensuite de décrire ce qu'il se passe quand on ajoute un élément x à un ensemble E afin d'obtenir une partie \( F = E \cup \{ x \}\) , en supposant que l'on connaît déjà l'ensemble des parties de E, soit  \( \mathcal{P}(E)\) . Si une partie de F contient x, il s'agit d'un élément de \( \mathcal{P}(E)\) auquel on ajoute x, sinon il s'agit d'un élément de \( \mathcal{P}(E)\) . Nous décrivons ainsi toutes les parties de F. Quand on ajoute un élément à E, on double donc le nombre de ses parties. Comme le vide n'a qu'une partie, par récurrence, on en déduit que, si E a un nombre fini n d'éléments, \( \mathcal{P}(E)\) possède 2ⁿ éléments. Cette méthode permet de plus de trouver l'ensemble des parties d'un ensemble fini quelconque. Voyons comment sur un cas simple.

Pour obtenir l'ensemble des parties de {1, 2, 3}, on part de  \( \mathcal{P}(\emptyset)=\emptyset\) , puis on considère \( \{ 1 \} = \emptyset \cup \{1\}\) , ce qui donne 

\( \mathcal{P}( \{ 1 \} )=\{ \emptyset, \{ 1 \} \}.\)

On considère ensuite \( \{ 1, 2 \} = \{ 1 \} \cup \{ 2 \} \) , ce qui fournit 

\( \mathcal{P}( \{ 1, 2 \} )=\{ \emptyset, \{ 1 \}, \{ 2 \}, \{ 1, 2 \} \}\)

On considère alors \( \{ 1, 2, 3 \} = \{ 1, 2 \} \cup \{ 3 \} \) , ce qui produit enfin 

\( \mathcal{P}( \{ 1, 2 \} )=\{ \emptyset, \{ 1 \}, \{ 2 \}, \{ 1, 2 \}, \{ 3 \}, \{ 1, 3 \}, \{ 2, 3 \} \)

Le théorème de Cantor

 Que se passe-t-il lorsque E est infini ? Le résultat suivant subsiste : \( Card(E)< Card(\mathcal{P}(E))\) , qui constitue le théorème de Cantor. L'inégalité large est évidente puisque l'on obtient une injection de E dans \( \mathcal{P}(E)\) en associant à tout élément x de E le singleton {x}. Pour démontrer que l'inégalité est stricte, on procède par l'absurde en supposant qu'il existe une bijection f de E sur \( \mathcal{P}(E)\) . On considère alors l'ensemble A des éléments x de E qui n'appartiennent pas à leur image par f, c'est-à-dire tels que \( x \notin f(x)\) .

Cet ensemble A est un élément de \( \mathcal{P}(E)\) . D'après l'hypothèse, il existe un élément x de E tel que A = f (x). Où est cet élément x par rapport à A ? Si x \( \in\) A, alors \( x \notin f(x)\) par définition, ce qui est absurde car A = f (x). Si x  \( \notin\) A, alors x \( \in\) f (x), ce qui est aussi absurde et prouve le théorème.

Une partie A de E est incluse dans une partie B de E, et on note \( A \subset B\) , si tous les éléments de A appartiennent à B. Il s'agit d'une relation d'ordre sur \( \mathcal{P}(E)\) , c'est-à-dire qu'elle est réflexive ( \( A \subset A\) ), antisymétrique ( \( A \subset B\) et  \( B \subset A\) impliquent A = B) et transitive ( \( A \subset B\) et  \( B \subset C\) impliquent  \( A \subset C\) ). Ainsi, \( \mathcal{P}(E)\) est un ensemble ordonné par l'inclusion.

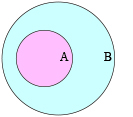
^{A est inclus dans B.}

Si A et B sont deux éléments de \( \mathcal{P}(E)\) , la réunion de A et B, notée \( A \cup B\) , est l'ensemble des éléments de E appartenant à A ou à B.

^{La réunion de A et de B.}

La réunion est associative : \( (A \cup B) \cup C = A \cup (B \cup C)\) .

Elle est commutative : \( A \cup B = B \cup A.\)

Elle possède la partie  \( \emptyset\) comme élément neutre : \( A \cup \emptyset=A.\)

De même, l'intersection de A et B, notée  \( A \cap B\) , est l'ensemble des éléments de E appartenant à A et à B. L'intersection est associative, commutative et E est un élément neutre.

L'intersection est distributive par rapport à la réunion : \( A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\) .

De même, la réunion est distributive par rapport à l'intersection : \( A \cup ( B \cap C) = (A \cup B) \cap (A \cup C).\)

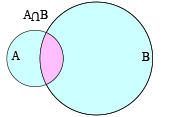
^{L'intersection de A et de B.}

Les lois de Morgan

Réunion et intersection s'échangent via les lois de Morgan, et la notion de complémentaire. Le complémentaire d'une partie A, notée A^C, est l'ensemble des éléments de E n'appartenant pas à A. Les lois de Morgan établissent que le complémentaire échange intersection et réunion :

\( (A \cap B)^C=A^C \cup B^C \rm{ et } (A \cup B)^C=A^C \cap B^C.\)

La différence de A et B, notée A \ B, est l'ensemble des éléments de A n'appartenant pas à B. Plus intéressante, la différence symétrique de A et B, notée A Δ B, est la différence de \( A \cup B\) et  \( A \cap B.\)

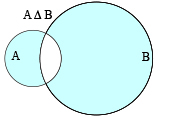
^{La différence symétrique de A et de B.}

La différence symétrique est associative, commutative et  \( \emptyset\)  est un élément neutre. De plus, chaque élément est son propre opposé : A Δ A = \( \emptyset\) . On en déduit que la différence symétrique est régulière, c'est-à-dire que A Δ B = A Δ C implique B = C. De plus, l'intersection est distributive par rapport à la différence symétrique. On en déduit que l'ensemble des parties de E muni de la différence symétrique (comme addition) et de l'intersection (comme multiplication) est un anneau commutatif unitaire. Cet anneau est un anneau de Boole car \( A \cap A = A\) .

De façon générale, un anneau unitaire A est un anneau de Boole si, pour tout élément x, x² = x. On démontre le résultat surprenant suivant (théorème de Stone) : tout anneau de Boole est isomorphe à un sous-anneau d'un anneau des parties d'un ensemble.