
Quand le rayon du cercle est un entier
À chaque triplet pythagoricien (a, b, c) peut être associé un triangle rectangle T. Son cercle inscrit possède un rayon qui est lui aussi un nombre entier. Par exemple, au triplet (3, 4, 5) est associé le triangle rectangle de côtés 3, 4 et 5, dont le cercle inscrit est de rayon r = 1. La valeur du diamètre r cherché est en fait donnée par la formule 2r = a + b – c si c désigne l'hypoténuse, avec a impair et PGCD(a, b) = 1.
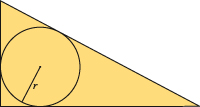
Ce joli résultat semble peu connu. On le trouve pourtant explicitement, proposé en exercice par Dominique Roux.
Il se démontre très bien par la caractérisation arithmétique des triplets pythagoriciens (voir ci-contre). Vous pouvez également vous amuser à retrouver le résultat de manière purement géométrique, en considérant un découpage astucieux de la figure faisant apparaître plusieurs triangles rectangles semblables !
Quoi de neuf en maths ? Pythagore !
Il faudrait dix milliards d'années à un être humain pour la lire, il a fallu deux jours à un supercalculateur pour la produire : il s'agit de la preuve du problème de la bicoloration des triplets de Pythagore. L'énoncé, resté sans réponse depuis les années 1980, est simple : est-il possible de colorier chaque entier positif en bleu ou en rouge, de telle manière qu'aucun triplet de Pythagore ne soit monochrome ? Autrement dit, aucun triplet (a, b, c) d'entiers vérifiant a2 + b2 = c2 ne doit être d'une même couleur : (3, 4, 5) étant un tel triplet, si 3 et 4 sont rouges, 5 ne peut pas l'être. Élaborée par les Américains Marijn Heule et Victor Marek et le Britannique Oliver Kullmann, c'est la plus longue preuve jamais construite à ce jour. En 200 téraoctets de données, qui leur ont permis d'étudier tous les cas possibles, compte tenu de réductions dues aux symétries du problème et de techniques de théories des nombres, les trois scientifiques ont répondu non : il est possible de colorier « comme il faut », et même de différentes façons, les entiers jusqu'à 7 824, mais il est impossible d'aller au-delà !
L'arithmétique élémentaire à la rescousse
Pour démontrer que le rayon du cercle inscrit à un triangle rectangle est un nombre entier (voir ci-dessus), matérialisons les trois bissectrices intérieures du triangle ; leur point de concours est, par définition, le centre O du cercle inscrit, renommé pour l'occasion cercle pythagoricien. Relions O aux trois points P, Q, R de tangence entre le cercle et le triangle. Les trois segments ainsi délimités sont de même longueur r (ce sont des rayons du cercle). Il s'agit donc d'établir que le rayon r du cercle pythagoricien est un entier.
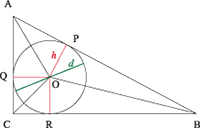
L'aire du triangle (rectangle) ABC est égale à la somme des angles des triangles (rectangles) AOB, AOC et BOC.
On obtient alors :
Mais comme (a, b, c) est un triplet pythagoricien primitif, on peut écrire a = p2 – q2, b = 2pq et c = p2 + q2, avec p et q deux entiers premiers entre eux (p ≥ q) et de parité différente. On en déduit alors aisément la valeur de r :
Le rayon du cercle pythagoricien est donc bien un entier, et on vérifie par ailleurs que (a + b – c) / 2 = pq – q2 = q(p – q) = r.
Le résultat est complètement démontré !