Le théorème connu de nos jours sous le nom de « théorème de Pythagore » apparaît dans sa forme définitive, pour ce qui concerne la géométrie plane, comme la proposition 47 du livre I des Éléments d'Euclide : dans tout triangle rectangle, le carré construit sur l'hypoténuse est équivalent à (de même aire que) la somme des carrés construits sur les côtés perpendiculaires.

La proposition suivante (numéro 48) est sa récipro­que : l'égalité des carrés implique que le triangle est rectangle. À aucun moment, Euclide n'associe le nom de Pythagore à ces deux propositions. Le texte contient une démonstration générale, illustrée par une figure chez Euclide, traduite ici en trois schémas. La démarche consiste à découper le carré construit sur l'hypoténuse en deux rectan­gles dont chacun a une aire égale à celle de l'un des carrés construits sur les côtés de l'angle droit.

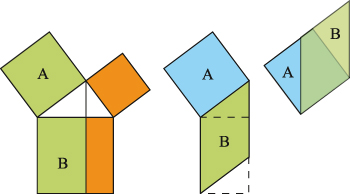
_{Il suffit de démontrer que A = B, l'autre égalité s'ensuivant par symétrie. Les deux transformations (à droite) de la partie B permettent de le prouver.}

Des origines mésopotamiennes

Dans la marge du bas, le copiste a ajouté, en guise de commentaire, un dessin représentant une démonstration plus facilement compréhensible, mais valable seulement dans un cas particulier, celui où le triangle rectangle est isocèle. Elle évoque le Ménon de Platon, écrit un siècle avant Euclide, toujours sans mention de Pythagore. Socrate y décrit la figure suivante, qu'on l'imagine avoir été tracée sur le sable : 

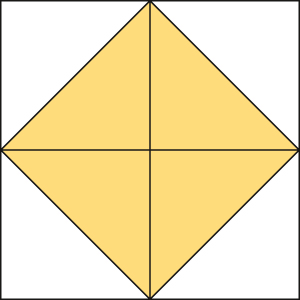 ^{En comptant les triangles, on montre que le carré (de biais et en jaune) construit sur l'hypoténuse est le double des petits carrés.} 

 À partir de là, il est aisé de voir que l'aire du grand carré est le double de celle du carré de biais, en jaune. Cette figure nous fait remonter le temps de plus d'un millénaire, car le plus ancien vestige archéologique évoquant le théorème de Pythagore date de deux mille ans avant notre ère, et vient de Mésopotamie. Il s'agit d'une tablette d'argile pouvant tenir dans la paume d'une main, probablement un travail d'étudiant selon les archéologues, un exercice à résoudre contenant un énoncé et un résultat, comme toutes les autres tablettes à caractère mathématique retrouvées dans cette région.

^{Tablette YBC 7289 (Yale Babylonian Collection, université de Yale).}

On y voit un carré divisé en quatre triangles rectan­gles isocèles. D'après le théorème de Pythagore, la diagonale est égale au côté du carré multiplié par la racine carrée de 2. La tablette contient également trois nombres écrits en cunéiforme :

Enquête sur une tablette

La difficulté, comme toujours dans la numération babylonienne, est que l'unité n'est pas précisée ! En analogie anachronique avec le système actuel, on pourrait dire que la virgule n'a pas été placée… ce qui est normal puisqu'elle ne sera introduite que plusieurs millénaires plus tard, à la Renaissance. En essayant plusieurs possibilités, on remarque que, si l'on place la virgule après le premier chiffre, ce nombre vaut 305 470 / 60³ (soit 1,414212963…), ce qui constitue une excellente approximation de la racine carrée de 2 (environ 1,414213562). La différence d'un petit millio­nième entre ces deux nombres rend notre hypothèse très vraisemblable. Décrypté de la même manière, le second nombre donne 152 735 / 60² (soit 42,42638889…), qui est le produit de 30 par la racine carrée de 2. La diagonale du carré est donc ce second nombre, et non le premier ! Vu ainsi, l'exercice semble porter sur la multiplication par 30, ce qui revient, dans ce système de base 60, à diviser par 2 (comme multiplier par 5 revient à diviser par 2, puis décaler les chiffres, dans le système décimal). On trouve bien le résultat indiqué sur la tablette, et on imagine que le but de l'exercice pouvait être là.
Rien ne permet de dire comment la valeur de \( \sqrt{2}\) avait été obtenue, peut-être était-elle donnée par le maître. Une autre tablette contient des éléments pouvant servir à construire des triangles rectangles à côtés entiers, sans plus de commentaires.

^{La tablette Plimpton 322, du nom de George Arthur Plimpton, qui l'avait achetée avant d'en faire don à l'université de Columbia. Les nombres de la colonne de gauche sont partiellement effacés donc difficiles à prendre en compte.}

Cela signifie-t-il que les Babyloniens connaissaient le théorème de Pythagore dans sa généralité ? Impossible de conclure en l'absence de toute autre preuve. Ainsi, il est difficile de dater le théorème de Pythagore de façon précise dans le monde recouvrant la Grèce et le Proche-Orient antique. Sans doute a-t-il été découvert et démontré dans sa généralité au moins un siècle avant Euclide, à l'époque de Platon, qui l'évoque dans plusieurs configurations dans le Timée. Plus à l'est, les Chinois comme les Indiens ont également découvert le théorème de Pythagore dans l'Antiquité, au moins dans certains cas particuliers. Les Indiens le nomment théorème de la diagonale et les Chinois théorème du Gougu (ce terme désigne une configuration). Voici la démonstration que l'on trouve dans le Chou Pei, le plus ancien traité mathématique chinois (qu'il est difficile de dater, mais qui est probablement antérieur à Euclide). Cette figure correspond à une démonstration, contrairement à celles des tablettes babyloniennes, mais cette démonstration n'est pas directement généralisable, ce qui peut faire soupçonner que le cas général n'était pas envisagé.
 

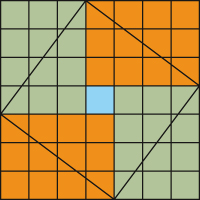
^{Démonstration du théorème de Pythagore dans le cas du triangle (3, 4, 5). Chaque rectangle a pour surface douze petits carrés donc le triangle, qui en est la moitié, six, ce qui fait vingt-cinq pour le carré en biais au milieu. Son côté est donc égal à 5.;}

Dans un commentaire du Chou Pei, Liu Hui (III^e siècle) propose une démonstration générale, malheureusement sans figure, dont les explications écrites font penser à un puzzle. Un mathématicien indien du XII^e siècle, Bhaskara, généralise l'idée du Chou Pei dans une démonstration également en forme de puzzle.
 

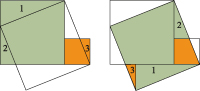
^{Puzzle de Liu Hui : en déplaçant les triangles numérotés 1, 2 et 3, on constitue le grand carré à partir des deux petits.}

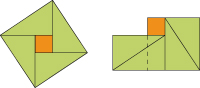
^{Le puzzle de Bhaskara.}

La preuve la plus simple du théorème nous vient aussi de la tradition indienne, sans qu'on puisse facilement la dater. Certains la font remonter à l'ère védique (I^e et II^e millénaires avant notre ère), ce qui ne correspond pas à l'histoire ultérieure vue ci-dessus : si le théorème avait été découvert dans sa généralité à l'époque védique, pourquoi les documents ultérieurs ne donneraient-ils que des cas particuliers ?

^{La démonstration védique est mi-géométrique, mi-algébrique. D'après la décomposition du grand carré, de côté a + b, de la figure, ( a + b )2 = c 2 + 2 ab, ce qui se simplifie en a2+ b2= c2.}

Cette démonstration peut sonner étrangement moderne puisqu'elle conclut sur la formule a² + b² = c². Cela vient essentiellement de notre écriture anachronique de la partie algébrique. Le théorème n'a pas évolué avant le XIX^e siècle mais a vu plusieurs centaines de démonstrations visant soit la clarté, soit l'originalité, soit l'esthétique. De ce point de vue, la plus belle est sans doute celle que nous devons à Léonard de Vinci.

^{La démonstration due à de Vinci : les quatre quadrilatères ABJE, BCDJ, ACIG et GFHI sont égaux. Or la somme des deux premiers est égale au grand carré plus deux triangles et la somme des deux seconds aux deux petits carrés plus deux triangles. On en déduit le résultat.}

Vers une écriture algébrique

Aujourd'hui, le théorème s'énonce en oubliant les carrés au sens géométrique : dans un triangle rectangle, si a et b sont les longueurs des côtés de l'angle droit (les cathètes) et c la longueur de l'hypoténuse (le côté opposé à l'angle droit), alors a² + b² = c². Réciproquement, si a, b et c sont les longueurs des trois côtés d'un triangle et qu'elles vérifient la relation a² + b² = c², alors le triangle est rectangle et c est la longueur de l'hypoténuse.

L'esthétique est allée de la beauté graphique ou de la simplicité vers l'adéquation à la raison profonde du théorème. Avec les idées de Felix Klein exposées dans le programme d'Erlangen (selon lesquelles la géométrie est plus liée aux questions de groupes d'invariants qu'aux figures elles-mêmes), on préférera des démonstrations comme celle qui suit. Soit ABC un triangle, rectangle en A, et H le pied de la perpendiculaire menée de A sur (BC). Les trois triangles ABC, AHB et CHA sont semblables car leurs angles sont égaux.

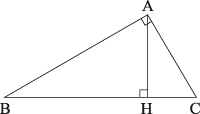
L'invariance des rapports de longueurs dans les similitudes entraîne trois égalités, dont la première est

\( \frac{AB}{BH}=\frac{BC}{AB}.\)

Elle donne le carré de la longueur AB comme produit de BC et de BH. De même, la suivante donne le carré de AC. En faisant la somme de ces deux égalités, on obtient AB² + AC² = BC(BH + HC) = BC². Le théorème de Pythagore apparaît alors comme une conséquence de l'invariance des rapports de longueurs en géométrie euclidienne.

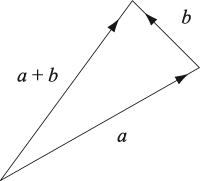
L'écriture algébrique du théorème a l'avantage de se généraliser aux espaces euclidiens, c'est-à-dire aux espaces vectoriels réels, munis d'un produit scalaire. Par définition, deux vecteurs y sont orthogonaux si, et seulement si, leur produit scalaire est nul. La démonstration du théorème de Pythagore se résume alors au calcul suivant :

|| a + b ||² = (a + b | a + b) = || a ||² + 2(a | b) + || b ||².

Si a et b sont deux vecteurs orthogonaux, (a | b) = 0, d'où || a + b ||² = || a ||² + || b ||², ce qui constitue l'énoncé du théorème de Pythagore dans les espace euclidiens. Les applications du théorème de Pythagore dans les espaces euclidiens, de fonctions par exemple, sont nombreuses et inattendues.