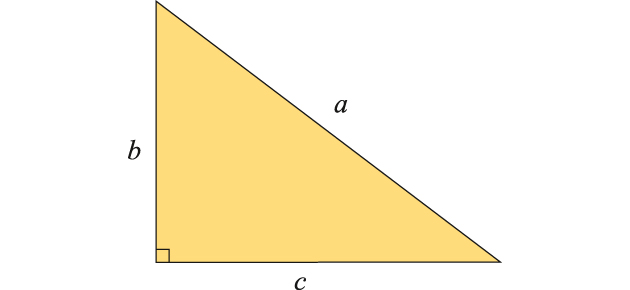
D'après le théorème de Pythagore, si a est l'hypoténuse d'un triangle rectangle, b et c les côtés de l'angle droit, a² = b² + c². On parle de triplets pythagoriciens si ces trois nombres sont des entiers pour une certaine unité de mesure. Dans ce cas, le triangle est rationnel dans le sens que les rapports de ses côtés sont des nombres rationnels. Réciproquement, un triplet pythagoricien correspond à un triangle rectangle rationnel.

Fermat : une remarque visionnaire

Le plus célèbre des triplets pythagoriciens, (3, 4, 5), correspond à la corde à treize nœuds utilisée par les bâtisseurs du Moyen Âge pour tracer des angles droits.

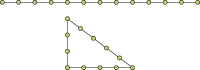
^{La corde à treize nœuds.}

Ces triplets peuvent être entièrement décrits en suivant la démarche que Diophante utilise pour résoudre le problème qu'il pose dans le livre II de son Arithmétique : « Partager un carré proposé en deux carrés. »
Les solutions de cette énigme constituent les triplets pythagoriciens, qui se trouvent également chez Euclide, mais sous forme géométrique. L'originalité de Diophante est de poser et de résoudre la question de manière purement arithmétique. En marge du texte de Diophante, dans la traduction latine de Bachet de Méziriac (1581–1638), Fermat nota : « Au contraire, il est impossible de partager soit un cube en deux cubes, soit un bicarré en deux bicarrés, soit en général une puissance quelconque supérieure au carré en deux puissances de même degré : j'en ai découvert une démonstration véritablement merveilleuse que cette marge est trop étroite pour contenir. » Il s'agit du fameux théorème de Fermat, qui est resté une conjecture jusqu'à la démonstration donnée en 1995 par Andrew Wiles. Vu que la preuve de Wiles s'étend sur plusieurs centaines de pages, et qu'aucune autre preuve substantiellement moins sophistiquée n'a été proposée depuis, on peut douter que Fermat ait réellement trouvé une démonstration, merveilleuse ou pas. Mais sa note marginale aura suscité un nombre considérable de recherches mathématiques durant trois cents ans, c'est là tout son intérêt historique et scientifique !
La méthode de Diophante, comme celle d'Euclide, conduit à une infinité de solutions, qui se paramètrent de la façon suivante :

a = (p² + q²)r, b = 2 pqr et c = (q² – p²)r,

où p et q sont deux nombres entiers premiers entre eux tels que 0 < p < q et r est un nombre entier strictement positif. Ces formules permettent de dresser une liste de triplets pythagoriciens. Il est facile de vérifier que l'on obtient ainsi des triplets pythagoriciens, il est plus difficile de prouver qu'on les obtient tous.

Un peu d'arithmétique

 La méthode purement arithmétique de Diophante ne donne pas de signification aux paramètres p, q et r. Ce sens est géométrique. On considère donc un triangle rectangle rationnel ABC, son cercle inscrit et t la tangente du demi-angle θ au sommet B. Les relations dans le triangle OBK (voir le schéma) donnent r = t BK = t (c – r). Comme BK = BC – CJ et CJ = AC – AJ, BK = a – b + r, d'où a – b + r = c – r. On en déduit 2r = b + c – a et 2BK = a – b + c, d'où t = (b + c – a) / (a – b + c).
La relation

montre que t est rationnel et, comme b = a sin B et c = a cos B, 

Ainsi, un triangle rectangle est rationnel si, et seulement si, la tangente de l'un de ses demi-angles au sommet, hormis l'angle droit, est rationnelle. Comme t < 1 (puisque θ < π / 4) et que t est rationnel, il existe deux nombres entiers p et q premiers entre eux tels que 0 < p < q et t = p / q, donc

Enfin, p² + q² et pq sont premiers entre eux : en effet, supposons qu'ils aient un facteur premier commun, d. Comme ce diviseur divise le produit pq, d'après le théorème de Gauss, il divise ou p, ou q. Supposons que cela soit d. Comme d divise p² + q², il divise donc q² et il divise également q, ce qui est contradictoire avec PGCD(p, q) = 1. Ainsi les nombres p² + q² et pq sont premiers entre eux.
Par conséquent, si l'un des deux nombres p et q est pair, l'autre est impair et p² + q² est premier avec 2pq, donc il divise a. Il existe par conséquent un nombre entier m tel que a = m(p² + q²), d'où b = 2mpq et c = m(q² – p²). Comme a, b et c sont premiers entre eux, m = 1, a = p² + q², b = 2pq et c = q² – p².
Si les deux nombres p et q sont impairs, on pose q' = (p + q) / 2 et p' = (q – p) / 2. Les nombres p' et q' ne sont alors pas tous les deux impairs et on retrouve les formules précédentes en changeant p et q en p' et q' et en échangeant b et c. On en déduit que a = p'² + q'², c = 2p'q' et b = q'² – p'². Donc, si (a, b, c) est un triplet de nombres premiers entre eux tel que a² = b² + c², alors il existe deux nombres entiers premiers entre eux p et q, dont l'un est pair, tels que a = p² + q² et les entiers (b, c) sont 2pq et q² – p². La preuve est bouclée !