Ce texte est issu de la conférence de Marie-Claude Arnaud donnée le mercredi 10 février 2016 dans le cadre du cycle de conférences « Un texte, un mathématicien » à la Bibliothèque Nationale de France.
Marie-Claude Arnaud est professeure à l'université d'Avignon et des pays du Vaucluse.
Jürgen Kurt Moser est né le 4 Juillet 1928 à Königsberg, alors en Prusse. Il ne pouvait naître sous de meilleurs auspices : la ville est bien connue des mathématiciens par le problème des ponts de Königsberg, qui a inspiré Euler et lancé deux domaines mathématiques, la topologie et la théorie des graphes.
L'arrivée au pouvoir des nazis en 1933, puis la guerre rendent la jeunesse de Moser difficile et périlleuse. Il est longtemps séparé de ses parents, survit par miracle et doit aller, pour la majeure partie à pied, sous le feu des soldats et des forces de police soviétiques, de Königsberg à Göttingen. Là, il peut intégrer le département de mathématiques en 1947. Le mathématicien Franz Rellich (1906-1955) le prend sous son aile et reconnaît vite son talent : Moser obtient sa thèse en 1952 sur la théorie spectrale des opérateurs différentiels. Puis Carl Siegel l'intéresse à la théorie des nombres et à l'astronomie, et particulièrement au problème des n corps (l'étude du comportement de n masses ponctuelles soumises deux à deux à l'attraction newtonienne).
« Une grande confiance en lui »
Grâce à une bourse américaine d'excellence Fulbright, Moser passe l'année 1953 à l'Institut Courant à New York. Son collègue à l'Institut, Peter Lax, dit de lui : « Nous réalisâmes qu'il était vraiment spécial, un prince parmi les hommes, un chevalier dans son armure étincelante… Il travaillait dur, aimait les sports de plein air, la beauté, la musique. Il était un excellent camarade. Il aimait l'aventure et tester sa puissance ; il avait une grande confiance en lui. » Un autre de ses élèves, plus tard son collègue, Paul Rabinowitz (né en 1939), affirme qu'il était « une de ces rares personnes qui ont le don de voir les mathématiques dans leur ensemble. Moser était attentif à leurs relations avec d'autres sciences. Ses recherches ont eu un profond impact à la fois sur les mathématiques, l'astronomie et la physique ».
Titre de l'article de Moser sur le problème de la stabilité du système solaire publié en 1978 dans le premier numéro de Mathematical Intelligencer.
La question de la stabilité du système solaire hante les mathématiciens depuis que Newton a publié la loi d'attraction universelle à la fin du XVIIe siècle. Cette loi d'attraction est pourtant de formulation très simple.
Pour deux planètes, une solution exacte existe et est unique : c'est la trajectoire elliptique connue de Kepler. Mais pour plus de deux planètes, les solutions explicites font généralement défaut : on a longtemps pensé qu'il était impossible de prédire le comportement à long terme des planètes du système solaire. Aussi le drame couvait : une planète pouvait-elle être éjectée du système solaire ? ou au contraire s'approcher du soleil pour que, selon les termes de Jürgen Moser, « il ne lui arrive malheur » ?
Cette question a mené à des résultats très profonds, qui sont probablement plus importants que la réponse à la question posée. Le « théorème KAM » (énoncé par Andreï Kolmogorov en 1954, démontré rigoureusement par Vladimir Arnold en 1963 et retrouvé indépendamment par Jürgen Moser à la même époque) indique que, dans certaines conditions restrictives, les planètes restent sagement sur des orbites confinées.
Le théorème KAM et la stabilité du système solaire
Les forces entre les planètes causent des perturbations et la forme des ellipses change peu à peu. Joseph-Louis Lagrange et Siméon Denis Poisson prouvèrent au XIXe siècle la stabilité des trajectoires, mais en ne considérant que les premiers termes des perturbations. Si l'on s'intéresse seulement à ce qui se passe pendant quelques dizaines d'années ou siècles, leurs calculs sont corrects, mais ils ne permettent de tirer aucune conclusion sur ce qui adviendra dans plusieurs millions d'années.
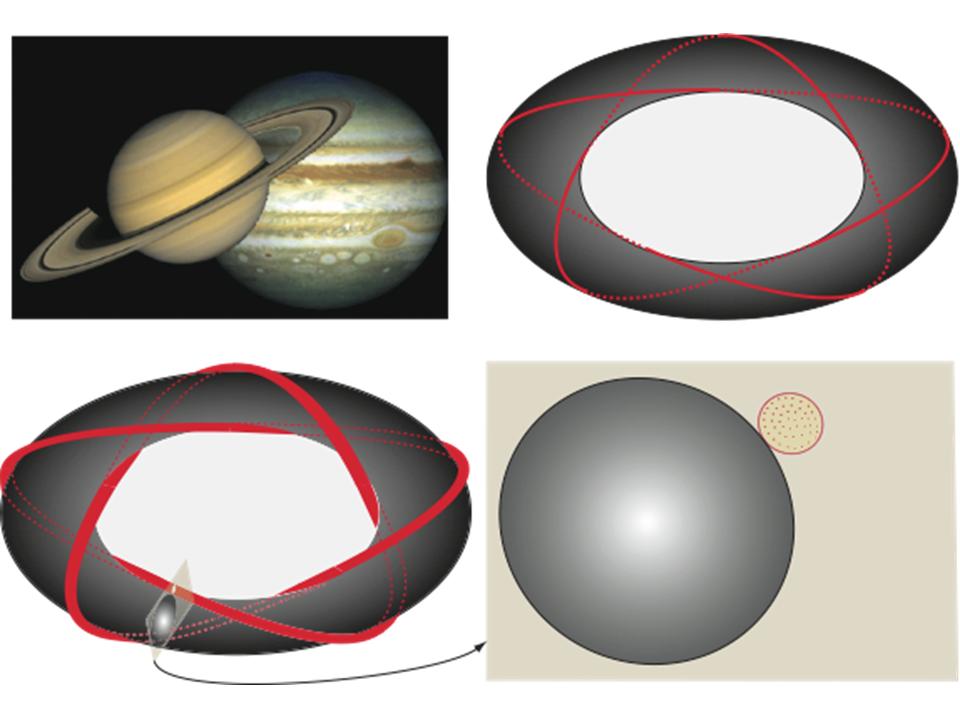En haut, à gauche : le couple Jupiter–Saturne.
En haut, à droite : en rouge, la trajectoire du couple Jupiter–Saturne sans interaction représentée sur un tore.
En bas : les solutions quasi stationnaires démontrées par le théorème KAM (la trajectoire est confinée dans un tore, figuré en rouge, centré autour de la trajectoire sans interaction).
Le cas le plus inquiétant pour la stabilité du système solaire est celui du couple Jupiter-Saturne : leurs années sont dans le rapport 2/5 (ce qui signifie que Saturne tourne deux fois autour du Soleil pendant que Jupiter réalise cinq révolutions). Aussi, les deux planètes se retrouvent périodiquement dans la même position relative et il se pourrait que la répétition de leur attraction mutuelle dans cette position amplifie les modifications de leurs orbites, comme la résonance que l'on observe quand on pousse un enfant sur une balançoire. Ainsi, la théorie des nombres s'introduit dans la dynamique céleste !
Mathématiquement ce rapport rationnel de deux cinquièmes se traduit par le « problème des petits diviseurs ». Ces petits diviseurs apparaissent aux dénominateurs des termes perturbatifs (utilisés pour approximer les solutions du mouvement des planètes, les termes perturbatifs peuvent ainsi devenir arbitrairement grands et rompre la belle harmonie horlogère du système solaire). L'étude du mathématicien français Henri Poincaré en avait conclu qu'il n'y avait pas de trajectoires stables pour n corps en interaction gravitationnelle (voir Tangente SUP 63-64).
Le résultat de Poincaré, qui avait convaincu des générations de mathématiciens, n'en était pas moins erroné ! L'existence de trajectoires quasi périodiques stables est annoncée en 1954 au Congrès international des mathématiciens : Kolmogorov y affirme que, sous certaines conditions, la majorité des trajectoires sont stables (celles contenues dans des « îles de stabilité » entourées d'un univers chaotique). L'idée de base, selon Jürgen Moser, est d'inventer une technique d'itération qui converge tellement vite que l'on peut contrôler l'effet cumulatif des petits diviseurs.
L'ergodicité n'est pas une fatalité
L'effet cumulatif est évité, pour certaines conditions initiales, lorsque le rapport des années des planètes est un nombre diophantien (c'est-à-dire mal approximable, mais ceci est une toute autre histoire). La portée du théorème KAM est immense. Jürgen Moser écrivait en 1975 : « Le développement de la mécanique statistique avait incité à croire que la plupart des systèmes mécaniques, au moins ceux qui sont composés de beaucoup de particules, sont ergodiques, c'est-à-dire qu'après un intervalle de temps suffisant, leur comportement est entièrement indépendants des conditions initiales. » Heureusement les mathématiciens se trompaient, sinon nous autres habitants du système solaire ne serions peut-être pas là !
La non-ergodicité a un impact important sur la stabilité des faisceaux de protons dans les grands accélérateurs de particules : les protons accomplissent des milliards de révolutions dans un anneau de stockage et, pour que les trajectoires soient contrôlées, les constructeurs de tels anneaux doivent se préoccuper des conditions de validité du théorème KAM.