Les nombres premiers sont une source intarissable de surprises mathématiques : ils sont infinis mais rares et, quand on veut les dénombrer, on voit apparaître des fonctions transcendantes, comme la fonction zêta de Riemann, a priori très éloignées de l'arithmétique.
Le mathématicien norvégien Atle Selberg.
Traditionnellement, les nombres premiers sont définis comme les nombres sans diviseur autre qu'eux-mêmes et l'unité. Pour éviter d'y inclure le nombre 1, de nos jours, cette définition s'écrit souvent de la façon suivante : un nombre premier est un entier ayant exactement deux diviseurs.
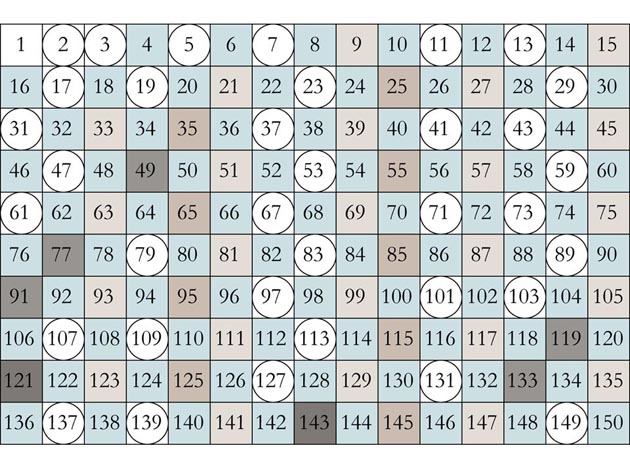
Dans l'Antiquité, Ératosthène (276-194 avant notre ère) a montré comment déterminer les nombres premiers inférieurs à un nombre donné, en éliminant tous ceux qui ne le sont pas (voir Tangente 149). Par exemple, pour connaître la table de tous les nombres premiers inférieurs à 150, on commence par dresser la table de tous les nombres de 2 à 150. On garde 2, qui est premier, et on supprime ses multiples, ce qui ne demande aucun calcul : il suffit en effet de se déplacer de deux en deux dans la table. On recommence avec le premier nombre non supprimé, c'est-à-dire 3, en opérant de même, et ainsi de suite. On obtient le tableau ci-dessous.
Crible d'Ératosthène : les multiples de 2 sont teintés en bleu clair, ceux de 3, 5, 7 et 11 sont en couleurs de plus en plus foncées. Les nombres premiers, repérés par des cercles, restent en blanc.
Limpide, simple et si belle…
La construction d'Ératosthène montre que tout nombre possède au moins un diviseur premier et, en itérant ce raisonnement, qu'il se factorise de manière unique en un produit de nombres premiers. De nos jours, ce théorème porte le nom de théorème fondamental de l'arithmétique. Il est probable qu'Euclide, légèrement antérieur à Ératosthène, n'en connaissait pas davantage. Pourtant, il s'est posé une question très abstraite concernant les nombres premiers : sont-ils en nombre limité ? Sa réponse fut : « Non. » Elle était accompagnée d'une démonstration limpide. Transcrivons-la en termes modernes, mais sans y introduire la délicate notion d'infini, qu'Euclide évitait soigneusement :
➔ L'ensemble des nombres premiers est plus grand que tout sous-ensemble de nombres premiers donné.
Son idée pour le démontrer est à la fois belle et simple : il multiplie entre eux tous les nombres a, b, c… de ce sous-ensemble fini, et leur ajoute 1. Ce nouveau nombre, abc… + 1, admet un diviseur premier p. Si ce nombre faisait partie de l'ensemble considéré, par exemple s'il était égal à a, il diviserait à la fois abc… + 1 et abc…,
donc leur différence, qui est 1, ce qui est absurde. Donc p n'appartient pas à l'ensemble de départ. L'ensemble des nombres premiers est donc illimité ! Pour décrire ce fait, on parle d'infini potentiel car toute limite peut être dépassée. En termes modernes, on dit simplement que l'ensemble des nombres premiers est infini.
La construction du crible d'Ératosthène permet également de s'apercevoir que les nombres premiers, relativement courants dans la première ligne (six sur quinze entiers), se raréfient ensuite progressivement. Cette raréfaction a suscité des recherches sur leur répartition, en particulier sur l'étude de la fonction π qui, à chaque valeur de
n, associe le nombre de premiers inférieurs à n. Cette fonction peut être tabulée, ce qui demande de nombreux calculs (tableau 1).
Une table de ce genre a sans doute aidé Adrien-Marie Legendre (et semble-t-il également Gauss, voir l'encadré) à conjecturer, puis à montrer que le rapport
}{n})
tendait vers zéro quand
n tendait vers l'infini. De façon étonnante, il a alors introduit une fonction qui n'a
a priori rien à voir avec l'arithmétique, la fonction logarithme népérien, notée
ln, en conjecturant que π (n) était équivalent à
Cela resta longtemps une conjecture, avant de devenir le théorème des nombres premiers quand il fut démontré un siècle plus tard, en 1896, par Jacques Hadamard (1865-1963), et indépendamment par Charles-Jean de la Vallée Poussin (1866-1962), en utilisant des techniques a priori très détournées. Il faudra attendre Atle Selberg (1917-2007) et Paul Erdös (1913-1996) pour en trouver une preuve « élémentaire » (ce qui ne veut pas dire qu'elle soit simple, mais seulement qu'elle n'utilise pas l'analyse complexe). Ce théorème s'énonce également en disant que le nième nombre premier pn est asymptotiquement équivalent à n ln n (tableau 2).
Des pépites arithmétiques
Des renseignements suffisamment précis sur la fonction π permettent de prouver de jolis résultats. Par exemple, en 1845, Joseph Bertrand (1822-1900) conjectura que l'écart entre un nombre premier et son successeur ne peut être supérieur au nombre duquel on est parti (postulat de Bertrand). Le prouver revient à montrer qu'il existe toujours au moins un nombre premier entre n et 2n, c'est-à-dire que π (2n) – π (n) > 0.
La conjecture de Legendre permet de l'exprimer à travers le calcul des valeurs de la différence
égale à
, )
qui devraient donc toutes être positives si n ≥ 2. Pour assurer le résultat, il a fallu attendre 1849 et une célèbre inégalité établie par Pafnouti Tchebychev (1821-1894) !
Voici l'inégalité en question :
 \leq1,106 \frac{n}{\ln n})
pour n ≥ 30.
Toujours pour n ≥ 30, cette inégalité permet de minorer
-\pi(n))
par
\( 0,921\frac{2n}{\ln 2n} - 1,106 \frac{n}{\ln n}\)
soit
,)
puis d'en déduire qu'il est strictement positif, ce qui entraîne le postulat de Bertrand. Ainsi, des renseignements sur π(n) permettent de prouver des résultats concernant les nombres premiers. Une amélioration de l'évaluation asymptotique de π(n) permet, par exemple, de démontrer que l'intervalle [1, n] contient plus de nombres premiers que [n, 2n] (pour n assez grand).
Un coup d'œil suffit pour constater que nous sommes très loin d'une estimation exploitable en pratique pour déterminer le nième nombre premier !
Bernhard Riemann (1826-1866) a trouvé un lien entre la répartition des nombres premiers et la fonction que l'on nomme depuis fonction zêta de Riemann, ce qui est encore plus surprenant que l'irruption des logarithmes dans cette question purement arithmétique. Sur la droite réelle, ζ(x) est définie comme la somme
=1+\frac{1}{2^x}+\frac{1}{3^x}+\ldots+\frac{1}{n^x}+\ldots)
L'étude du sens de cette somme montre que zêta est définie sur l'intervalle réel ]1, +∞[ et qu'elle tend vers l'infini quand x tend vers 1. La théorie des fonctions analytiques permet d'étendre la définition de cette fonction au plan complexe privé du point 1.
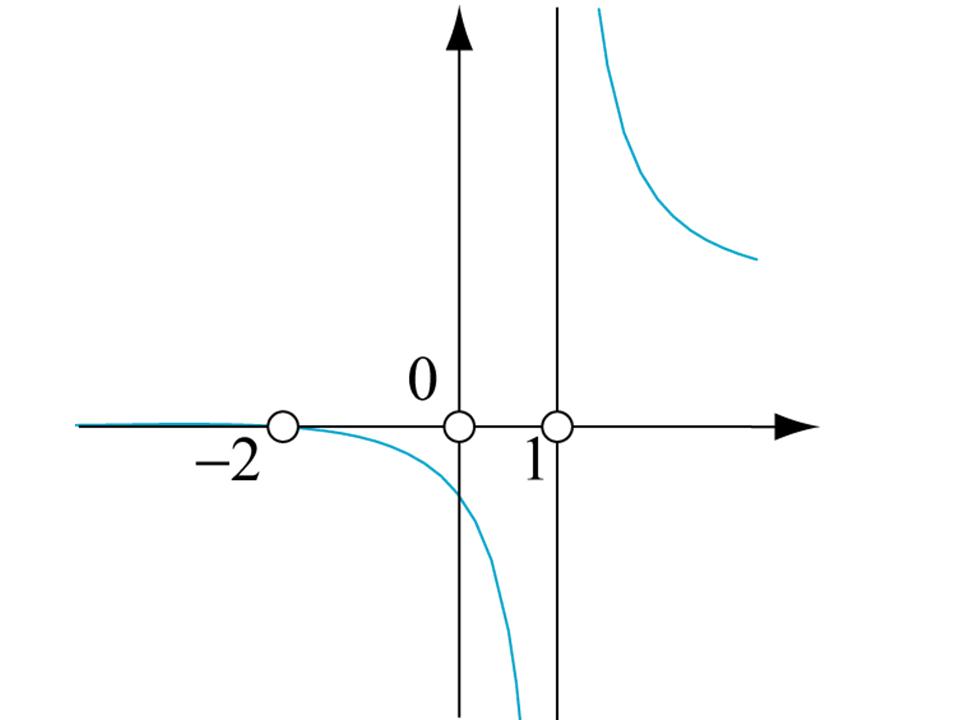Représentation de la fonction zêta de Riemann
dans le plan réel. Elle a une asymptote en x = 1.
Cette fonction a des zéros réels : les nombres entiers pairs négatifs (–2, –4, –6, –8, …). Comme ils sont faciles à trouver, on les dit triviaux. La fameuse hypothèse de Riemann concerne les autres : les zéros non triviaux de la fonction zêta sont tous imaginaires, de partie réelle égale à 1 / 2.
Même si cette hypothèse a été vérifiée pour les 1013 premiers zéros, elle reste une conjecture, c'est-à-dire que personne n'a réussi à la démontrer. Il s'agit de l'un des sept problèmes du millénaire, que l'Institut Clay a dotés d'un prix d'un million de dollars. Quelles seraient les conséquences possibles d'avancées dans la connaissance intime des zéros de la fonction zêta ? On peut en espérer la résolution de conjectures célèbres sur les nombres premiers, une meilleure connaissance des nombres premiers (et de nombreux autres domaines des mathématiques), ou des progrès importants dans la factorisation des nombres entiers. Ceci aurait des conséquences pratiques : le secret du chiffre protégeant les transactions bancaires, comme les messages ou paiements sur Internet, est fondé sur la difficulté de cette factorisation. Cependant, la seule résolution de l'hypothèse de Riemann serait loin d'y suffire.
Amélioration
L'approximation de π(n) du théorème des nombres premiers peut être améliorée en introduisant la fonction logarithme intégral, notée Li, définie par
=\int_2^x \frac{dt}{\ln t})
et, bien entendu, asymptotiquement équivalente à x / ln(x).
Reprenons la table du début (les valeurs non entières sont arrondies) :
|
n
|
10
|
100
|
1 000
|
10 000
|
100 000
|
1 000 000
|
10 000 000
|
|
π(n)
|
4
|
25
|
168
|
1 229
|
9 592
|
78 498
|
664 579
|
|
n / ln n
|
4
|
22
|
145
|
1 086
|
8 686
|
72 382
|
620 421
|
|
Li(n)
|
5
|
29
|
177
|
1 245
|
9 629
|
78 626
|
664 917
|
Li(n) approche mieux π(n) que n / ln n. Cette approximation n'est cependant toujours pas exploitable pour déterminer de grands nombres premiers.
Malgré de spectaculaires progrès récents (voir Tangente 153 et Tangente 170), la répartition des nombres premiers reste insaisissable… et fascinante.
