
Au XVIIe siècle, pour concevoir un bateau, on n'effectuait que peu de calculs, et les navires n'étaient pratiquement pas construits sur la base de plans. Seuls la longueur, la largeur, ainsi que d'éventuels chargements, étaient pris en compte dans le cadre des contrats entre le client et le constructeur. On réalisait des modèles réduits dont on conservait les proportions. Ces méthodes de travail traditionnelles, ainsi que les constructions navales toujours hasardeuses, furent à l'origine de nombreuses catastrophes.
 L'un des naufrages les plus spectaculaires fut celui du navire de guerre suédois le Vasa, construit par le roi Gustave II Adolphe de Suède, de la dynastie des Vasa, entre 1626 et 1628. Le Vasa était un trois-mâts de 69m de long, 52,5m de haut et 11,7m de large. Il pesait 1 210 tonnes et embarquait soixante-quatre canons de gros calibre. L'équipage comptait cent quarante-cinq hommes. Le 10 août 1628, lorsque le navire quitta le port pour la première fois, il chavira brusquement, se renversant sur le côté, et coula en l'espace de quelques minutes.
L'un des naufrages les plus spectaculaires fut celui du navire de guerre suédois le Vasa, construit par le roi Gustave II Adolphe de Suède, de la dynastie des Vasa, entre 1626 et 1628. Le Vasa était un trois-mâts de 69m de long, 52,5m de haut et 11,7m de large. Il pesait 1 210 tonnes et embarquait soixante-quatre canons de gros calibre. L'équipage comptait cent quarante-cinq hommes. Le 10 août 1628, lorsque le navire quitta le port pour la première fois, il chavira brusquement, se renversant sur le côté, et coula en l'espace de quelques minutes.
En 1628, nous sommes quinze ans avant la naissance d'Isaac Newton. L'absence de la théorie de la gravitation rendait impossible toute théorie rigoureuse de la stabilité du navire. Le roi avait, d'une part, constamment modifié la taille du bateau durant sa construction, si bien que les proportions étaient faussées. D'autre part, des canons supplémentaires avaient été montés, de sorte que le centre de gravité du navire se déplaça beaucoup plus haut que prévu. Si les théories de Bouguer et d'Euler en hydrostatique et en hydrodynamique avaient pu être appliquées à cette époque, cette catastrophe aurait été évitée.
À l'origine, Archimède
 L'exemple du Vasa illustre l'importance qu'il faut accorder à la stabilité lors de la conception du navire. C'est à Archimède que l'on doit les fondements de l'hydrostatique. Il faudra cependant attendre le XVIIIe siècle pour avoir une définition rigoureuse du métacentre avec le volumineux Traité du navire, de sa construction et de ses mouvements de Pierre Bouguer, publié en 1746.
L'exemple du Vasa illustre l'importance qu'il faut accorder à la stabilité lors de la conception du navire. C'est à Archimède que l'on doit les fondements de l'hydrostatique. Il faudra cependant attendre le XVIIIe siècle pour avoir une définition rigoureuse du métacentre avec le volumineux Traité du navire, de sa construction et de ses mouvements de Pierre Bouguer, publié en 1746.
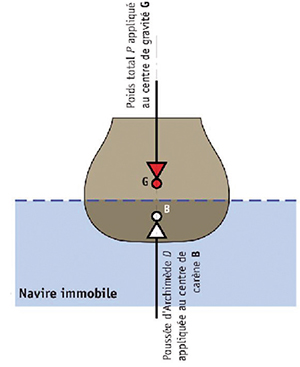
L'hydrostatique étudie le navire immobile, sa flottabilité et sa stabilité. Un bâtiment flotte lorsque son poids est égal au poids de la masse d'eau déplacée par la partie immergée. Autrement dit, il est à l'équilibre quand les vecteurs poids et poussée d'Archimède sont de même module et alignés sur le vecteur gravité, c'est-à-dire la verticale.
La surface de flottaison est l'intersection du plan de mer avec le volume du navire. Deux flottaisons d'un même navire sont isocarènes si elles délimitent des carènes de géométries différentes mais de même volume. Le déplacement d'un objet à bord d'un navire peut générer une variation d'inclinaison isocarène. Cette propriété d'apparence triviale a son importance. Lorsque l'on incline le flotteur, le poids reste le même. Ainsi, le volume vi qui vient d'être immergé doit être égal au volume ve qui vient d'être émergé. Ce qui se traduit par l'équation vi = ve. Ces deux volumes pour de petits angles ont la forme d'un onglet.
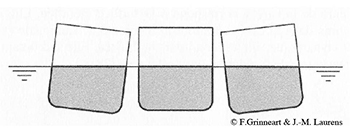 Illustration de flottaisons isocarènes. L'inclinaison du flotteur peut être représentée soit incliné par rapport à une surface libre horizontale, soit à plat par rapport à une surface libre inclinée.
Illustration de flottaisons isocarènes. L'inclinaison du flotteur peut être représentée soit incliné par rapport à une surface libre horizontale, soit à plat par rapport à une surface libre inclinée.
Le schéma ci-dessus représente le flotteur dans un plan d'inclinaison (c'est-à-dire tout plan perpendiculaire à l'axe d'inclinaison). Dans un monde bidimensionnel, deux flottaisons isocarènes « assez proches » l'une de l'autre (écartées d'un « petit » angle) se coupent au centre de la ligne de flottaison : il n'y a qu'un axe possible pour faire passer les flottaisons isocarènes. En 3D, ce n'est pas le cas. Avec les hypothèses des petits angles et des flottaisons isocarènes se posait depuis longtemps cette question : les différents axes d'inclinaison se coupent-ils tous en un même point ? C'est Leonhard Euler qui répond de manière rigoureuse à cette question, en démontrant en 1749 le théorème suivant :
L'intersection de deux flottaisons isocarènes infiniment voisines passe par le centre de gravité de chacune de ces flottaisons.
Le métacentre et la stabilité
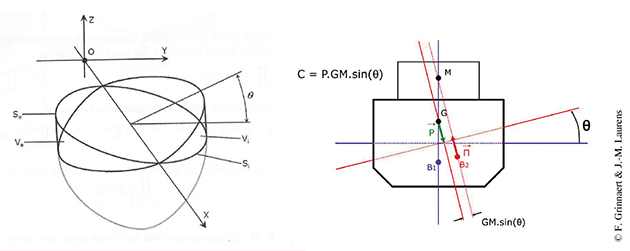
Considérons le navire à l'équilibre vertical. Les points B1 et G sont alignés sur la même verticale terrestre, confondue avec la verticale du repère lié au navire. On fait subir une inclinaison isocarène d'un angle infiniment petit au navire. Le centre de carène B1 se déplace en B2. La verticale terrestre subit une rotation équivalente dans le repère lié au navire. Elle n'est plus confondue avec la verticale du navire. Le point M d'intersection des verticales terrestres passant par le centre de carène avant inclinaison B1 et après inclinaison B2 est appelé le métacentre. B2 et G n'étant plus sur une même verticale terrestre, le navire n'est plus à l'équilibre. Il apparaît alors un couple de redressement, proportionnel à la hauteur métacentrique GM.
La notion de métacentre est donc la clé de la stabilité du navire. La position de ce point dépend de la position du centre de carène, et de la géométrie de celle-ci. Dans la pratique, on limite les études à l'examen des inclinaisons autour des axes transversal et longitudinal. Si l'inclinaison du navire est transversale (variation de gîte), le métacentre est appelé transversal (tvsl). Si l'inclinaison du navire est longitudinale (variation d'assiette), le métacentre est longitudinal.
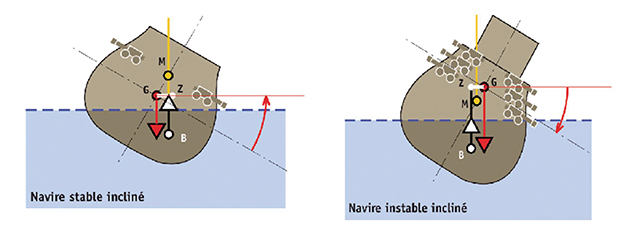
L'étude de la stabilité initiale (ou stabilité aux petits angles) permet de déterminer si l'équilibre du flotteur est stable. On pose le navire à plat sur l'eau. Pour qu'il y ait équilibre stable, il faut non seulement que les points B et G soient alignés sur la verticale, ce qui suppose une carène et une répartition des poids étudiées, mais également que GM > 0. Si l'équilibre initial n'est pas stable, le moindre déplacement angulaire autour de cette position déséquilibre le navire : le couple de rappel est négatif.
Ces principes de base permettent de réaliser des courbes de stabilité du navire étudié, qui doivent répondre à des critères précis pour satisfaire la règlementation en vigueur.
Ferry, paquebot et catamarans
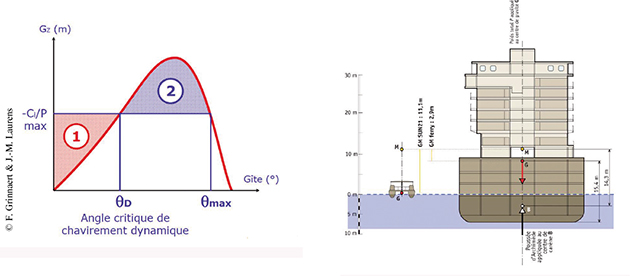
Quelle est la hauteur métacentrique du paquebot transatlantique Queen Mary 2 construit au chantier naval de Saint-Nazaire il y a quelques années ? Les plans d'un navire ne sont pas du domaine public. Voici une coupe typique, aimablement mise à disposition par l'architecte naval Guillaume Lagrée. La hauteur métacentrique transversale de ce ferry mesure 2,9m. À ses côtés, le catamaran SUN21 est le premier bateau solaire à avoir traversé l'Atlantique (en mai 2007). Grâce à ses deux coques, il a un métacentre élevé (GMtvsl = 11,1m), ce qui lui confère une grande stabilité.
 Construite en 1919 pour ravitailler Paris en charbon depuis Rouen, la péniche Louise-Catherine est en ciment armé. Achetée par l'Armée du Salut en 1929, elle est confiée la même année à Le Corbusier pour sa transformation en asile flottant d'une centaine de lits. Depuis 1995, le bateau est désaffecté. Pour préserver ce patrimoine, un groupe de jeunes architectes rachètent le Louise-Catherine en 2006 pour en faire un centre dédié à l'architecture. Selon les architectes navals François Grinnaert et Jean-Marc Laurens, le calcul de la stabilité d'une barge en béton est en tout point identique à celui d'un navire classique. Il faut connaître : la géométrie précise du flotteur (plan des formes), la masse ou le tirant d'eau, la position du centre de gravité (au moins sa coordonnée verticale). Si la géométrie du flotteur est simple, ce calcul peut être manuel. Dans le cas contraire, on utilise un logiciel spécialisé avec lequel on crée un modèle 3D.
Construite en 1919 pour ravitailler Paris en charbon depuis Rouen, la péniche Louise-Catherine est en ciment armé. Achetée par l'Armée du Salut en 1929, elle est confiée la même année à Le Corbusier pour sa transformation en asile flottant d'une centaine de lits. Depuis 1995, le bateau est désaffecté. Pour préserver ce patrimoine, un groupe de jeunes architectes rachètent le Louise-Catherine en 2006 pour en faire un centre dédié à l'architecture. Selon les architectes navals François Grinnaert et Jean-Marc Laurens, le calcul de la stabilité d'une barge en béton est en tout point identique à celui d'un navire classique. Il faut connaître : la géométrie précise du flotteur (plan des formes), la masse ou le tirant d'eau, la position du centre de gravité (au moins sa coordonnée verticale). Si la géométrie du flotteur est simple, ce calcul peut être manuel. Dans le cas contraire, on utilise un logiciel spécialisé avec lequel on crée un modèle 3D.
 Selon François Grinnaert et Jean-Marc Laurens : « Respecter une hauteur métacentrique initiale positive pour le navire à l'état intact est loin d'être suffisant pour le mettre à l'abri du naufrage. Il est certes impossible de garantir un risque zéro mais un minimum de confiance dans le navire est nécessaire, surtout pour les assureurs. L'historique de la création des sociétés de classification retracé dans le livre de Philippe Boisson, Politiques et Droit de la sécurité maritime (Bureau Veritas, 1998), rappelle qu'elles sont nées des besoins de l'assurance maritime au début du XIXe siècle. La motorisation des navires ne les a pas rendus plus sûrs. Les incendies et les naufrages dus à une perte de stabilité après avarie sont particulièrement lourds en pertes humaines quand il s'agit de navires à passagers. Il a fallu l'impact médiatique du Titanic pour que la première convention Safety Of Life At Sea voie le jour. »
Selon François Grinnaert et Jean-Marc Laurens : « Respecter une hauteur métacentrique initiale positive pour le navire à l'état intact est loin d'être suffisant pour le mettre à l'abri du naufrage. Il est certes impossible de garantir un risque zéro mais un minimum de confiance dans le navire est nécessaire, surtout pour les assureurs. L'historique de la création des sociétés de classification retracé dans le livre de Philippe Boisson, Politiques et Droit de la sécurité maritime (Bureau Veritas, 1998), rappelle qu'elles sont nées des besoins de l'assurance maritime au début du XIXe siècle. La motorisation des navires ne les a pas rendus plus sûrs. Les incendies et les naufrages dus à une perte de stabilité après avarie sont particulièrement lourds en pertes humaines quand il s'agit de navires à passagers. Il a fallu l'impact médiatique du Titanic pour que la première convention Safety Of Life At Sea voie le jour. »