
Paradoxalement, la fondation de l'Observatoire royal de Greenwich en 1675 par le roi Charles II d'Angleterre est due à un Français, M. de Saint Pierre, qui réclama en 1675 une récompense pour une nouvelle méthode de calcul des longitudes. Le roi demanda l'arbitrage de l'astronome britannique John Flamsteed (1646-1719), qui ne .jpeg) L'un des plus grands bronzes du monde
L'un des plus grands bronzes du monde
Le cône du planétarium de l'observatoire de Greenwich est l'une des plus grandes pièces de bronze au monde. Il est constitué d'environ deux cent cinquante plaques de bronze, épaisses de 8 mm, assemblées et patinées, pour donner l'impression qu'il est fondu d'une seule pièce. Ces plaques ont été fabriquées à Gateshead (dans la banlieue de Newcastle, dans le Nord-Est de l'Angleterre) et transportées à Londres, dans le quartier de Greenwich, pour assemblage sur une structure de béton.
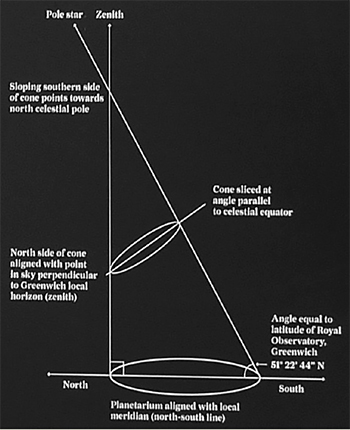
.jpeg) La forme du cône en elle-même, comme il convenait en ce lieu dédié à l'astronomie, est reliée aux étoiles. Le côté Nord du cône est aligné avec la perpendiculaire à Greenwich et la pente Sud dirigée vers l'Étoile polaire ; un raisonnement de géométrie élémentaire permet de montrer que pour que la génératrice Sud pointe vers l'Étoile polaire elle doit faire avec l'horizontale du lieu un angle exactement égal à la latitude de l'observatoire de Greenwich, soit 51°28'44”. En effet, cela donne exactement l'angle de visée sur l'Étoile polaire (actuellement Alpha Ursae Minoris), qui est dans le prolongement de l'axe polaire Nord-Sud sur la voute céleste.
La forme du cône en elle-même, comme il convenait en ce lieu dédié à l'astronomie, est reliée aux étoiles. Le côté Nord du cône est aligné avec la perpendiculaire à Greenwich et la pente Sud dirigée vers l'Étoile polaire ; un raisonnement de géométrie élémentaire permet de montrer que pour que la génératrice Sud pointe vers l'Étoile polaire elle doit faire avec l'horizontale du lieu un angle exactement égal à la latitude de l'observatoire de Greenwich, soit 51°28'44”. En effet, cela donne exactement l'angle de visée sur l'Étoile polaire (actuellement Alpha Ursae Minoris), qui est dans le prolongement de l'axe polaire Nord-Sud sur la voute céleste.
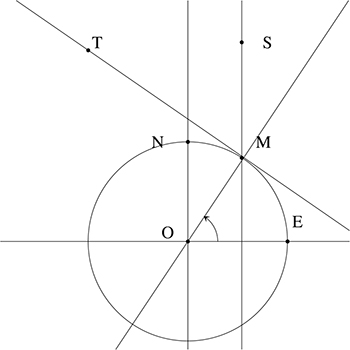 . Mais cet angle est aussi égal à
. Mais cet angle est aussi égal à car ils ont des côtés deux à deux perpendiculaires, d'où le résultat
La géométrie du cône
Notre cône est à base circulaire, engendré par les droites (génératrices) reliant un sommet fixe S à un point d'un cercle (appelé la directrice du cône) tracé dans le plan horizontal. Pour le géomètre, il fait partie d'une famille de surfaces plus vaste : un cône C de sommet S est une partie de l'espace telle que, pour tout point M de C différent de S, la droite (SM) soit incluse dans C. Dans la pratique, le cône est déterminé par une courbe, que l'on peut choisir plane, appelée la directrice D du cône, et par son sommet S. Il est alors formé de toutes les droites (SM) lorsque M parcourt D.
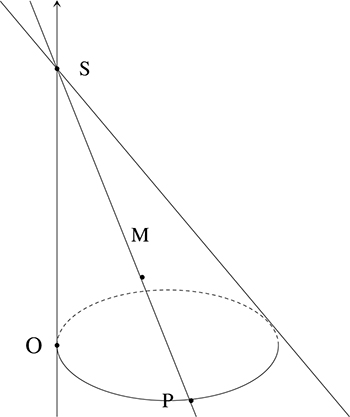
La particularité de ce cône est que son sommet S, dans la direction zénithale du lieu, est donc situé sur l'axe (Oz). Il admet donc des coordonnées de la forme (0, 0, h), avec h = OS. L'équation du cercle dans le plan (Oxy) est :
Un point M (x, y, z) appartient au cône s'il existe un point P (a, b, 0) du cercle tel que la droite (SM) passe par P. Cela se traduit par l'existence d'un réel t tel que l'on ait x = at, y = bt, et z – h = – th.
En écrivant que (a, b, 0) est sur le cercle, on obtient :
ou encore .
Mais comme , il vient :
soit
On a bien obtenu l'équation du cône du planétarium de l'observatoire de Greenwich !
Lire la suite