Les nombres réels sont insuffisants en algèbre. Pour produire des résultats esthétiques et généraux, il faut étendre leur corps en le complétant au moyen de nombres dits imaginaires, qui furent introduits par Cardan et Bombelli dès le XVI^e siècle. Leur but ? Résoudre des équations polynomiales à coefficients réels de manière complète et générale. L'extension se fait en prenant en considération un nombre imaginaire, « i », qui est défini par la curieuse propriété i² = –1. Le concept de nombre est alors étendu en dimension 2 en construisant des objets de la forme a + bi (a et b sont réels), que l'on baptise nombres complexes. Ces nombres s'additionnent et se multiplient (ou se divisent) sans difficulté et l'ensemble des nombres complexes peut ainsi être érigé en corps commutatif (pour employer un terme technique). Dès le XIX^e siècle, la structure géométrique de ces nombres a été largement étudiée, notamment par Gauss et Cauchy.

Visualiser l'addition et la multiplication

Le nombre complexe z = a + bi peut être représenté par le point du plan de coordonnées cartésiennes (a, b). Le passage aux coordonnées polaires permet d'écrire ce même point sous la forme , avec (la longueur du point z à l'origine) et , ce dernier (qui représente l'angle avec l'axe des abscisses) appartenant par convention à la fourchette [0, 2[. En adoptant ces notations, tout nombre complexe peut s'écrire . Enfin, grâce aux découvertes de Leonhard Euler, on peut écrire. Cette façon de voir permet d'illustrer géométriquement l'opération de multiplication d'un ou de plusieurs nombres complexes : les « longueurs » ou modules (r) se multiplient alors que les angles ou « arguments » s'additionnent. De manière ramassée :

Si les nombres réels peuvent être représentés sur une droite infinie, les nombres complexes peuvent être figurés sur le plan usuel muni de son origine ! Le nombre complexe a + bi a simplement pour coordonnées (a, b).

La propriété d'addition des arguments peut être observée également en se souvenant des formules de fonctions trigonométriques de sommes d'angles ! On calcule en effet :

soit encore

La notion de racine prend de ce fait, dès que l'on entre dans le monde complexe, des allures géométriques tout à fait intéressantes. Calculer la racine n-ième d'un nombre complexe revient, d'une part, en ce qui concerne son module, à calculer la racine équivalente dans les réels positifs, et d'autre part à déterminer le ou les argument(s) dont les multiples par n coïncident avec celui du nombre dont on veut calculer la racine, en se souvenant évidemment que les angles sont définis modulo .

Ainsi, soit un nombre complexe dont on souhaite calculer toutes les racines n-ièmes. Il faut donc résoudre l'équation Zⁿ = z. Le module de toute solution doit évidemment être égal à r^1/n. Comment déterminer tous les arguments correspondant à toutes les solutions ? Le premier auquel on pense est évidemment . Mais ce n'est pas le seul. On peut également prendre en considération et ainsi de suite. Attention, dès que l'on considère , on retombe sur la solution initiale… modulo . Les solutions à retenir sont donc les suivantes :

Le cas le plus simple : z = 1 

Dans le cas particulier des racines énièmes complexes de z = 1, appelées racines de l'unité, les résultats sont particulièrement esthétiques et s'interprètent géométriquement. On a en effet et . Comment se distribuent alors les solutions de l'équation particulière Zⁿ = 1 ? Notre solution générale donne immédiatement :

La première solution est évidente. Les autres seront le plus souvent complexes, sauf dans le cas des racines d'ordre pair, pour lesquelles la solution s = –1 va apparaître comme un nombre complexe particulier. Géométriquement, tous les points retenus se trouvent sur un cercle centré en l'origine et de rayon 1 (tous les modules sont égaux à 1) : ils forment un polygone régulier à n côtés. Les arguments parcourent la suite arithmétique 0, 2/n, 4/n… 2(n – 1)/n, pour revenir à 0 modulo . 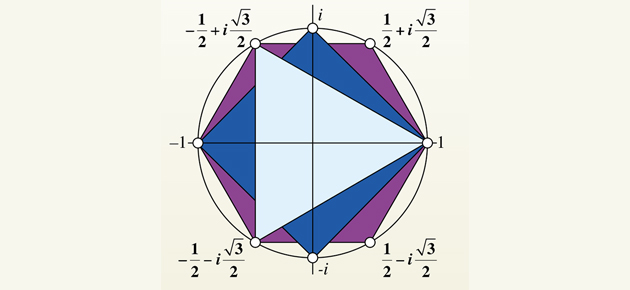Regardons en particulier les racines cubiques et quatrièmes, pour lesquelles les arguments conduisent à des valeurs trigonométriques élémentaires et ouvrent les portes à de nouvelles notions. Pour les racines cubiques, le polygone généré est un triangle isocèle (en bleu clair sur le graphique).

On a immédiatement :

On peut vérifier par calcul que 

Ces deux solutions engendrent chacune l'ensemble de toutes les solutions par puissances successives, ce qui n'est pas le cas de la solution dite « triviale » s₁. Les deux solutions complexes sont donc plus intéressantes ! Elles sont en fait solutions d'une équation secondaire construite à partir d'un polynôme dit cyclotomique. On peut décomposer le polynôme à coefficients entiers Z³ – 1 en (Z – 1)(Z² + Z + 1). En l'annulant, le premier facteur donne naissance à la solution triviale (s = 1). Le polynôme cyclotomique associé est Z² + Z + 1, dont les racines sont s₂ et s₃.

Le terme « cyclotomique » est interprétable. Construite sur le terme grec tomê traduit par coupure (qui a donné l'adjectif tomikos signifiant propre à couper), judicieusement accouplée à kyklos signifiant cercle, l'appellation fait bien référence à la section du cercle en n secteurs identiques. Dans le cas du polynôme cyclotomique, seules les solutions qui génèrent la totalité des scissions (et donc des solutions à la racine n-ième) sont retenues.

Le passage à la résolution de l'équation polynomiale Z⁴ – 1 = 0 confirme cette interprétation géométrique. Le polygone associé est un carré (en bleu foncé sur le graphique). Les quatre solutions retenues sont s₁ = 1, s₂ = i, s₃ = –1 et s₄ = –i. Seules les solutions s₂ et s₄ vont engendrer les quatre solutions, par puissances successives.

L'équation de départ se décompose selon

Z⁴ – 1=(Z² – 1)(Z² + 1)=(Z – 1)(Z + 1)(Z² + 1) = 0.

Les deux premiers facteurs conduisent aux solutions réelles s₁ et s₃ alors que s₂ et s₄ sont solutions de l'équation Z² + 1 = 0, construite à partir du polynôme cyclotomique associé Z² + 1. Le graphique ci-dessus illustre les deux situations présentées, en ajoutant le cas de l'hexagone associé aux racines sixièmes. Dans cette configuration, seules deux parmi les quatre solutions complexes engendrent l'ensemble de toutes les solutions (celles qui ne sont pas solution de la racine cubique et qui ne coïncident pas avec l'un des sommets du triangle de départ) et le polynôme cyclotomique est de degré 2 : il s'agit de Z² – Z + 1. En effet, on tombe sur les décompositions successives suivantes :

Z⁶ – 1 = (Z³ – 1)(Z⁶ + 1) 

= (Z – 1)(Z² + Z + 1)(Z + 1) (Z² – Z + 1) = 0

Seul le dernier facteur égalé à zéro conduit aux deux solutions génératrices de… tout l'ensemble ! Étonnant non ?