Une demande constante des médecins est de connaître, sans intrusion, la cartographie des densités et interfaces internes d'un corps humain. Les principaux outils de contrôle non invasifs sont l'IRM et les tomogra­phies électron-positon, γ et X. Si ces examens d'imagerie médicale reposent sur des principes physiques différents, tous sont néanmoins totalement dépendants de traitements mathématiques pour compléter l'information, l'extraire du bruit et éliminer les artefacts.

IRM et scanner  

C'est le principe de base de l'IRMN anatomique. Ce sigle désigne l'Imagerie à Résonance Magnétique Nucléaire. L'adjectif Nucléaire en a été retiré pour ne pas affoler le patient qui, par ailleurs, demandera un panorama dentaire sans se poser de questions. 

L'IRM est un examen non destructif, contrairement aux autres techniques utilisant des rayonnements. Les traitements mathématiques de son fonction­nement sont néanmoins bien trop complexes pour être présentés ici. Les rayons, photoniques ou particulaires, traversent plus ou moins les corps selon leur énergie et la densité de la matière. Leurs interactions avec la matière provoquent donc un dépôt d'énergie, qui peut être nocif en cas de surexposition. Cet effet est d'ailleurs recherché pour « brûler » certaines tumeurs. Pour une radiographie médicale, utilisant des rayons X, l'image obtenue est une projection plane, sorte d'ombre chinoise où les os sont opaques, donc blancs, et les tissus légers noirs. Son interprétation est laissée à la compétence du clinicien. 

Le scanner est devenu le plus connu des tomographes. Ce terme vient de l'anglais to scan (scruter, balayer du regard), lui-même issu du latin scandere (monter degré par degré). On préconise en français les termes scanographe ou densitomètre, ou la triste francisation scanneur. Avec cet appareil, on effectue une série de radiographies dans différentes directions. Malgré tout, le rapport bénéfice/risque lié à l'irradiation est favorable au tomodensitomètre (TDM) par rapport à une radio, ce qui tend à en faire un examen complémentaire de l'IRM. La transformation numérique des données, l'inversion tomographique, nécessaire pour obtenir une image 3D, n'est possible que si l'information collectée est suffisante. Le principe mathématique du TDM repose sur le théorème de Radon (1917, voir encadré), dont l'application était impossible avant l'avènement des ordinateurs. 

Étude en dimension 2  

Dans le cas général, si le rayonnement X peut être considéré comme parallèle, le problème tomographique, initialement 3D, se ramène alors à un ensemble de tomographies 2D (voir figure).

Un objet à symétrie axiale est à deux dimensions, sa carte de densité dépend de sa position z sur l'axe de symétrie et de sa distance r à cet axe. Une coupe par un plan perpendiculaire à l'axe de symétrie est alors à une seule dimension. Une unique radiographie, de rayonnement parallèle et perpendiculaire à l'axe de symétrie, suffit alors pour effectuer la reconstitution tomographique de l'objet en entier. 

Expérimentalement, l'image est pixellisée. L'intensité  de chaque pixel correspond à l'intégration de l'objet le long d'un rayon X moyen. Ces rayons définissent des couches de l'objet dont l'épaisseur correspond à la taille d'un pixel. On peut alors essayer, en considérant la sphère constituée de telles couches homogènes, à la manière d'un oignon, d'inverser l'opérateur tomographique. Le rayon le plus extérieur (en noir sur la figure de la page précédente) donne directement la densité de la couche externe. Le rayon voisin traverse les deux couches externes (noire et verte), ce qui permet, en tenant compte du résultat précédent, d'obtenir la densité de la seconde couche. Nous avons en fait un système linéaire triangulaire qui s'inverse facilement de proche en proche. Malheureusement, la  méthode utilisée propage de couche en couche les erreurs qui s'accumulent sur l'axe de symétrie. C'est un problème mal posé, c'est-à-dire instable, qui nécessite des méthodes plus ou moins complexes de filtrages et régularisation.

Une application : la masse des boules 

Le calcul du volume d'une sphère dans un espace à n dimensions s'effectue classiquement par une intégrale multiple et nécessite une cascade de changements de variables qui, pour être triviaux, n'en sont pas moins lourds. La remarquable relation entre itérés de la transformée de Radon et opérateurs tomographiques permet d'obtenir ce résultat de façon originale en s'affranchissant de tels calculs.

Pour un corps à symétrie sphérique homogène, donc de fonction de densité d_R(r) = 1 pour r ≤ R, la transformée de Radon R donne la longueur traversée à la distance r du centre (voir encadré). En parti­culier, en r = 0, nous obtenons le diamètre .

Son itéré R² nous donne la somme de ces longueurs le long d'une direction perpendiculaire, c'est-à-dire la surface du cercle à la distance r du centre. En particulier, en r  =  0, nous obtenons la surface du grand cercle  .

A chaque itération, nous intégrons le long d'une dimension supplémentaire et nous obtenons, à l'origine, le volume de la sphère dont la dimension correspond à l'ordre d'itération de l'opérateur R, .

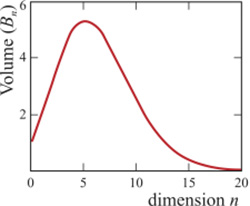On en déduit directement le volume d'une boule unité de dimension n :   ce qui nous prouve sa décroissance lorsque la dimension tend vers l'infini (voir la courbe). La boule unité se filamente le long des axes des coordonnées.

Ces remarques sont encore valables pour un corps à symétrie sphérique et de densité quelconque, en remplaçant la notion de volume par celle de masse.

En particulier, pour un profil de densité,  la masse M de notre objet est . 

Dans le cas où l'information nous est donnée par une image tomographique 1D de l'objet, de profil radial  nous obtenons la masse de l'objet  par une simple intégration : 

 .

L'intégration étant une sommation, et les bruits de mesures étant souvent de moyenne nulle, ce procédé a le mérite de fournir d'excellent résultat avec des mesures bruitées. L'exploitation des idées d'Abel et de Radon si longtemps après leurs découvertes confirment, si besoin était, l'importance de développer toute connaissance pour elle-même, hors de toute finalité.