L'appellation « cancer » recouvre tout type de prolifération cellulaire anormalement importante au sein d'un tissu de l'organisme, qui finit par former une tumeur. Les cellules cancéreuses sont toutes supposées issues d'une seule cellule souche, génétiquement altérée, qui se divise indéfiniment de manière anarchique jusqu'à mettre la vie du sujet atteint en péril. Selon l'O.M.S., le cancer serait responsable de 15 millions de décès par an, soit un toutes les deux secondes environ. Dans le langage populaire, il est appelé crabe, ce qui, curieusement, se réfère à son étymologie. Le père de la médecine, Hippocrate (460–370 av. J.C.), diagnostiquant des grosseurs (ou tumeurs) chez certains patients, les nomma καρκινοι dont le sens premier est crabes. Le médecin romain Celse (env. 30 av. J.-C. env. 50 ap. J.-C.) traduisit le terme en cancer, signifiant effectivement crabe en latin. La cancérologie est parfois nommée oncologie. Le terme ογκο (littéralement masse) fut introduit par le médecin Claude Galien (130–200) pour désigner toute grosseur d'allure maligne.

Un traitement au cas par cas

Le cancer tue encore massivement. Face à cette hécatombe, il n'y a pas de cure miracle. Divers types de traitements ont été développés depuis des décennies. On distingue des traitements systémiques, agissant sur le corps du patient dans sa totalité, c'est le cas de la chimiothérapie qui va nous occuper dans la suite, et des traitements locorégionaux, traitant exclusivement la zone tumorale infectée comme la chirurgie ou la radiothérapie.

Le traitement par chimiothérapie demande un dosage adapté avec grande précision. Une dose insuffisante injectée au patient ne produira pas d'effet. Mais les produits injectés se révèlent également toxiques : une dose trop importante peut avoir des effets secondaires dramatiques, voire létaux et chaque individu réagit différemment aux injections. Le traitement doit donc être adapté au cas par cas. Ce problème est remarquablement décrit par Dominique Barbolosi qui précise pour un traitement spécifique, que « lorsque qu'un patient doit être traité par un médicament nommé méthotrexate l'objectif clinique est que la concentration du médicament atteigne un plateau donné pour lequel l'efficacité anti-tumorale est optimale et les effets toxiques acceptables ». Il faut donc procéder à des prélèvements sanguins sur tout sujet traité, afin de mesurer les effets de la molécule injectée et de quantifier objectivement son taux de concentration. Pour des raisons de confort, on limite généralement ce type de prélèvement à une ou deux prises de sang, ce qui rend l'usage d'un modèle indispensable. On injecte le médicament par voie intraveineuse et on mesure ensuite sa concentration dans le sang. Cette dernière évolue et est décrite par une certaine fonction c (t). Il faut déterminer une fenêtre thérapeutique [c_min, c_max], élaborée de sorte que le médicament soit d'efficacité optimale dès que c (t) > c_min, et qu'il ne soit pas trop toxique pour c (t) < c_max. Il faut ensuite adapter le débit des perfusions pour que la concentration du médicament évolue en demeurant à l'intérieur de cette fenêtre. 

En route pour la mise en équation

On peut voir le système sanguin du patient comme un volume constant V dans lequel on détecte une certaine masse m (t) de produit injecté. La concentration vaut alors c (t) = m (t) / V. Supposons que l'on injecte le produit selon un débit u (t). L'organisme du patient élimine progressivement une partie du produit injecté. La vitesse d'élimination c'est à dire la quantité par unité de temps, est supposée proportionnelle (à taux k) à la masse de produit présente dans le volume sanguin du patient. La quantité de produit éliminé pendant un petit intervalle ∆t peut ainsi se noter k.m (t).∆t. La variation de masse de produit présent dans le système sanguin du patient suit :

∆m ≈ k.m (t).∆t + u (t).∆t.

Divisons par ∆t et passons à la limite de façon à transformer notre équation en :

m'(t) = – k.m (t) + u (t).

En divisant par V, l'équation introduit le taux de concentration et l'on a :      c'est-à-dire une équation différentielle ordinaire linéaire non homogène. Pour des raisons d'interprétation, on introduit la notion de clairance C_l = kV, qui quantifie la capacité d'élimination du médicament d'une personne donnée par unité de temps et qui pourra être calibrée par deux prises de sang à intervalle de temps bien choisi. Le terme est dérivé de l'anglais clearance, signifiant littéralement (Harrap's) liquidation du stock. L'équation devient :         Pour des raisons pratiques, on convient de donner à u (t) la forme d'une fonction en escalier. En effet, une perfusion est installée à débit constant puis arrêtée dès que le niveau de concentration optimal est atteint. La perfusion est donc supposée active à taux constant pendant une certaine durée t₀, ce qui revient à poser u (t) = d dans l'intervalle [0, t₀]. La valeur d quantifie le débit de la perfusion, qui devient ensuite inactive avec u (t) = 0 pour t > t₀. Cette façon de faire nécessite de traiter le problème en deux fois mais rend l'équation relativement facile à résoudre (voir encadré).

La solution à laquelle on arrive est une fonction définie par morceaux. Pour des temps inférieurs à t₀, c'est-dire pour la période pendant laquelle la substance active est injectée, on modélise la concentration par :               (condition initiale : c (0) = 0).

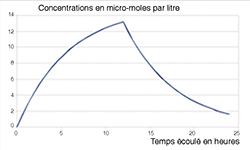
Cette fonction décrit une tendance à la saturation, la concentration croissant vers sa valeur maximale d / C_l, une valeur qui doit appartenir à la fenêtre thérapeutique et avoisiner la valeur optimale garantissant un traitement efficace. Mais il y a plus : une seule prise de sang effectuée après 6 heures et une seule mesure de concentration permet de calibrer la clairance par résolution d'une équation utilisée aussi en mathématiques financières et pour laquelle des méthodes de résolution sont connues. Enfin, en prenant en compte un temps de perfusion long (de l'ordre de 12 heures), on admet que la concentration se rapprochera du maximum. Soit c_P la concentration idéale. On peut déterminer le débit idéal de la perfusion en posant d = C_l.c_P. Dès que le niveau idéal est atteint, on arrête la perfusion (u (t) = 0). La concentration dans le sang suit alors l'équation différentielle homogène  sous de nouvelles conditions initiales, à savoir le niveau de concentration atteint en t = t₀. Cette équation exprime que la concentration décroît au taux C_l / V. Le graphique ci-contre donne une idée de l'allure générale de la fonction « concentration » pendant vingt-quatre heures alors que la perfusion a été active pendant douze heures.

On remarque que la seule connaissance de la clairance, un paramètre propre à chaque patient, permet de déterminer univoquement le débit optimal d. La subtilité du raisonnement est à la hauteur du défi que constitue la mise en place de méthodes de soins efficaces pour lutter contre le cancer. Mais tous les cancers ne guérissent pas. Ceci ne doit pas faire oublier que la prolifération des cellules cancéreuses suit une loi exponentielle et que la meilleure des stratégies contre cet envahisseur indésirable reste et demeure le dépistage précoce.