Courbes ROC

Le diagnostic d'une maladie se fait sur base d'un ensembles de critères. Le médecin peut aussi avoir recours à une batterie de tests afin de l'étayer. Il est rare qu'un test conduise à une conclusion certaine ; il peut se révéler positif sur un patient sain et négatif sur quelqu'un atteint par la maladie. Il est dès lors fondamental de connaître la capacité d'un test à discriminer entre la population des malades et celle des personnes saines. C'est la finalité de la courbe ROC, acronyme de la formulation anglaise Receiver Operating Characteristic, qui servit lors de la Seconde Guerre mondiale pour distinguer le bruit de fond marin du signal provenant de la présence d'un sous-marin ennemi. 

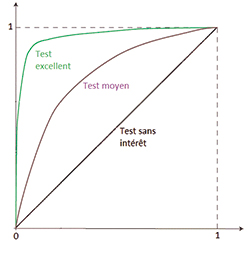
Un test déterminé se traduit par une mesure que l'on compare à un seuil. Pour toute valeur du seuil, la courbe ROC s'obtient en portant en ordonnée le taux de « vrais positifs » (fraction des positifs effectivement détectés) et en abscisse le taux de « faux positifs » (fraction des négatifs mal discriminés). 

Percentiles et quantiles

Soit un échantillon de mesures présentant un grand nombre de valeurs différentes. Dans le langage usuel, on dira que le percentile P_α ou « quantile d'ordre α » (0# α # 100) est la valeur de l'échantillon laissant α % des observations en dessous d'elle et (100 – α) % au-dessus.

Mais il convient de qualifier les inégalités associées aux termes en italiques au moyen des comparateurs « inférieur », « inférieur ou égal », « supérieur », « supérieur ou égal ».

Le plus connu des percentiles est P₅₀ qui correspond à la médiane. Pour définir correctement cette dernière, on peut dire qu'il y a au plus 50 % des observations strictement inférieures et au moins 50 % d'observations inférieures ou égales à P₅₀. Cette définition peut s'étendre à tous les percentiles. On distingue aussi les « quartiles » qui correspondent au percentiles P₂₅ et P₇₅. 

En termes de fonctions de répartition (pourcentage des observations inférieures ou égales à), on peut noter P_α = F ^–1 (α / 100). Dans le cas d'une variable discrète, la fonction de répartition est en escalier et sa fonction inverse n'est pas nécessairement univoquement définie. On convient alors de placer arbitrairement le percentile au « milieu » de la marche.

Courbes de croissance

Les courbes de percentiles sont utilisées en médecine pour contrôler la croissance des bébés. 

Ces courbes de croissance sont obtenues en calculant certains percentiles caractéristiques (voir la définition dans la brève ci-dessus), comme P₃, P₁₅, P₅₀, P₈₅, P₉₇, vus comme fonction du niveau du développement in utero d'un fœtus ou de l'âge d'un nouveau-né. 

Les plus connues sont celles qui furent établies par le docteur Lula Olga Lubchenco (1915–2001), dans les années 1960 à Denver aux États-Unis, pour tenter de caractériser différents paramètres des fœtus en fonction du nombre de semaines de gestation comme le poids, la taille, le périmètre crânien. 

Lorsque pour un âge gestationnel donné, la mesure observée sur un enfant est représentée par un point qui se situe à l'intérieur des courbes des percentiles P₃ et P₉₇, on considère généralement la croissance comme normale. Tout dépassement vers le haut ou vers le bas peut être le signe d'un développement atypique et être le marqueur d'une anormalité que ce soit un excès ou un retard de croissance. Mais il utile d'interpréter cette conclusion : quelle que soit la population considérée, éventuellement très homogène, il y aura toujours 3 % des individus présentant des mesures inférieures à P₃ et 3 % des individus présentant des mesures supérieures à P₉₇. De plus, des ensembles de mesures effectuées en différents lieux et à différentes époques ont donné naissance à des courbes significativement différentes. Il n'est donc pas si simple de déterminer si un enfant présente ou non de vrais problèmes de croissance.