Une notion géométrique insaisissable

Qu’est-ce qu’une courbe ?

Si l’on pose cette question à l’homme de la rue, on aura sans doute comme réponse que c’est « une ligne qui tourne ou qui a des arrondis ». Et à la question « une droite est-elle une courbe ? », sans surprise on aura une réponse négative, du genre « non, car elle ne tourne pas ».

On a le même genre de définition dans Le Robert, dictionnaire historique de la langue française : « Le mot “courbe” qualifie ce dont la forme, la direction ne comportent aucun élément droit ou plan, couramment et spécialement en géométrie. Il est employé comme substantif depuis la fin du XVII^e siècle avec son sens moderne. »

Quant au dictionnaire de langue française Larousse (sur Internet), il nous indique : « Ligne ou forme courbe », et à l’adjectif « courbe » : « qui s’infléchit sans contenir aucune portion de ligne droite ». C’est donc clair : dans le langage courant, étayé par les définitions des dictionnaires, une courbe est une ligne qui tourne et qui ne contient pas de partie droite. En particulier, une droite ne peut être une courbe.

On trouve quand même dans le Larousse, en deuxième définition : « Représentation graphique de l’évolution d’un phénomène », puis, en définition spécialisée en géométrie : « Image dans un espace euclidien de dimension 2 ou 3 d’un intervalle de \( \mathbb{R}\)  par une application continue. » Là, on s’en approche… mais cela demande, quand même, quelques explications. On se limitera aux courbes planes, c’est-à-dire, en reprenant les mots du dictionnaire, celles contenues dans un espace euclidien de dimension 2.

Rendons aux Grecs

Chez les Grecs, dès le VI^e siècle avant notre ère avec Thalès, la géométrie se construit à l’aide d’une règle et d’un compas. Les droites et les cercles sont les figures fondamentales. Les problèmes doivent se résoudre à l’aide de ces outils et de ces figures. C’est le cas de « abaisser, à partir d’un point, la perpendiculaire à une droite » ou de « construire la bissectrice d’un angle ». Mais d’autres, posés au cours du siècle suivant, ont résisté. Ce sont :

• la quadrature du cercle : construire un carré dont l’aire est égale à celle d’un disque donné ;

• la duplication du cube : construire un cube dont le volume est double du volume d’un cube donné ;

• la trisection de l’angle : diviser un angle donné en trois angles de même mesure.

Il faudra attendre le XIX^e siècle pour qu’en 1837 le Français Pierre-Laurent Wantzel (1814–1848) démontre que les deux derniers problèmes sont insolubles en géométrie euclidienne (en utilisant uniquement règle et compas et un nombre fini de tracés). Enfin, en 1882, l’Allemand Carl Louis Ferdinand von Lindemann (1852–1939) démontre la transcendance du nombre π et donc l’impossibilité de la première construction.

Ne sachant pas tout cela, les Grecs ont tenté de résoudre ces problèmes par des constructions géométriques, faisant ainsi apparaître des courbes (voir article « Des courbes pour dépasser le compas »). Par exemple, Ménechme, au IV^e siècle avant notre ère, résout la duplication du cube par l’intersection de deux coniques, une parabole et une hyperbole. En fait, il ramène le problème à la recherche de deux moyennes proportionnelles x et y qu’il faut « intercaler » entre 1 et 2 : on cherche donc x et y tels que \( \frac{1}{x}=\frac{x}{y}=\frac{y}{2}\) , transformant ainsi le problème en la construction de l’hyperbole d’équation  \( y=\frac{2}{x}\)  et de la parabole d’équation y = x², puis de leur intersection. L’abscisse de ce point vérifie x³ = 2. Cela étant exprimé, bien sûr, avec nos notations modernes et synthétiques !

Hélas, une telle résolution n’est que graphique… et donc inexacte.

Les coniques étaient connues à l’époque comme intersection d’un cône et d’un plan, d’où leur nom de sections coniques. Elles furent longuement étudiées par Apollonius au III^e siècle avant notre ère. Ce n’est que bien après, en particulier avec Pappus au IV^e siècle, qu’elles seront définies à l’aide des notions de directrice et de foyer.

Pour la résolution des deux autres problèmes, il s’agit toujours d’une résolution graphique ; d’autres constructions sont proposées et donnent naissance à de nouvelles courbes, appelées mécaniques car construites à l’aide d’un dispositif mécanique. On peut citer la conchoïde de Nicomède, la spirale d’Archimède ou la quadratrice d’Hippias. Toutes ces constructions de l’Antiquité nous ont donné des exemples de courbes… mais pas encore de définition.

L’étape suivante est atteinte avec les mathématiciens arabes à partir du X^e siècle. Par exemple, Omar Khayyam (vers 1048 ; 1131) résout certaines équations, des degrés 3 et 4, à l’aide d’intersections de coniques, construction admise, à cette époque, au même titre que la règle et le compas. Il dénombre vingt-cinq classes d’équations de degré inférieur ou égal à 3 et, pour chaque classe d’équations, il précise les couples de coniques à utiliser. Les axes de symétrie choisis ne sont pas fortuits. On a ainsi des représentations graphiques avec des éléments qui préfigurent abscisse et ordonnée.

L’un de ses successeurs, Sharaf al-Din al-Tusi (vers 1135 ; vers 1213), étudie plus précisément ces courbes pour justifier de leur intersection : il s’intéresse alors aux propriétés de continuité, de convexité et aux comportements asymptotiques.

[encadre]

Une résolution en suivant Omar Khayyam

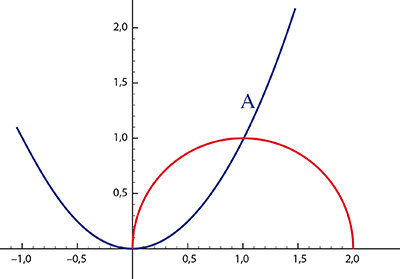
Pour résoudre l’équation x³ + ax = b (avec a > 0 et b > 0), Omar Khayyam la met sous la forme x³ + p²x = p²q. Il considère ensuite le cercle d’équation x² + y² = qx et la parabole d’équation x² = py. L’abscisse de A, l’un des points d’intersection de ces deux courbes, est une racine de l’équation initiale. Assurez-vous-en !

[/encadre]

Vers l’époque moderne

C’est Nicole Oresme (vers 1322 ; 1382) qui introduit explicitement le repérage des points du plan par des coordonnées, appelées par lui latitude et longitude. Il donne l’équation d’une droite à l’aide de ces dernières.

Deux siècles plus tard, au XVII^e siècle, la construction géométrique des racines des équations est un problème important étudié par les mathématiciens. René Descartes (1596–1650) trouve une construction pour résoudre les équations des degrés 3 et 4 à l’aide d’une parabole et d’un cercle. La résolution de ce problème essentiellement algébrique est facilitée par l’utilisation, dans son ouvrage fondamental Géométrie (1637), de deux axes perpendiculaires et des distances d’un point du plan à ces axes. Ces distances sont appelées par certains coupée (maintenant abscisse) et appliquée (maintenant ordonnée) et notées x et y. La géométrie analytique est née ! Une courbe est alors définie par une équation de la forme  f (x, y) = 0. C’est une évolution majeure ! 

Auparavant, avec Pappus en particulier, les courbes étaient classées en trois catégories : 

• les courbes planes : celles que l’on peut construire à la règle et au compas ;

• les courbes solides : les sections coniques, contenues dans le plan ;

• les courbes mécaniques (aussi appelées linéaires) : celles que l’on peut construire à l’aide d’instruments mécaniques comme les conchoïdes, les cissoïdes, les spirales…

Descartes propose une nouvelle classification :

• les courbes géométriques : celles où les deux coordonnées x et y vérifient une équation algébrique de la forme P (x, y) = 0 ; on les appelle maintenant courbes algébriques. Le degré du polynôme P donne le degré de la courbe algébrique : degré 2 pour les coniques, degré 3 pour les cubiques, degré 4 pour les quartiques… ;

• les courbes mécaniques : les autres (comme les spirales ou les cycloïdes), que l’on appelle maintenant transcendantes et que Descartes rejette de sa Géométrie, ne sachant pas les étudier de manière systématique. Ce sera l’affaire de ses successeurs !