
Le paradoxe de Richard
Prenons les vingt-six lettres de l’alphabet et ordonnons, par ordre alphabétique, tous les arrangements d’une lettre, de deux lettres, de trois lettres… Tout ce qui peut s’écrire se trouve dans la liste ainsi constituée. Biffons de ces arrangements tous ceux qui ne sont pas des définitions de nombres (Jules Richard parle de nombres réels) ; notons u1 le premier nombre de cette liste, u2 le deuxième… Ainsi, tous les nombres que l’on peut définir à l’aide d’un nombre fini de mots forment un ensemble dénombrable. Soit E l’ensemble des arrangements ainsi obtenus.
Richard affirme alors que l’on peut former un nombre n’appartenant pas à cet ensemble. Il nomme G le groupe de lettres suivant : « Soit p la énième décimale du énième nombre de l’ensemble E ; formons un nombre N ayant 0 pour partie entière, et pour énième décimale, p+1 si p n’est égal ni à 8 ni à 9, et l’unité dans le cas contraire. » Ce nombre N n’appartient pas à l’ensemble E puisque, s’il était égal à mettons un , son nème chiffre serait le nème chiffre décimal de un , ce qui n’est pas. Or, N est défini par les mots de G, c’est-à-dire un nombre fini de mots ; il devrait donc appartenir à l’ensemble E !

Russell et la consternation de Frege
Il semble que Bertrand Russell imagina son fameux paradoxe en juin 1901. Il en fait part à Gottlob Frege dans une lettre rédigée en allemand et datée du 16 juin 1902, suite à la lecture du premier volume de l’ouvrage Grundgesetze der Arithmetik (« Les lois fondamentales de l’arithmétique ») publié en 1893 par le logicien allemand :
« Il se trouve seulement un point où j’ai rencontré une difficulté. Vous affirmez qu’une fonction aussi peut agir comme l’élément indéterminé. Je l’ai pensé autrefois mais maintenant cette vision me semble douteuse à cause de la contradiction suivante. Soit w le prédicat “Être un prédicat qui ne peut se prédiquer lui-même”. De chaque réponse découle son opposée. En conséquence, nous pouvons conclure que w n’est pas un prédicat. »
Frege se rend compte que ce paradoxe remet en cause son souhait de fondation de l’arithmétique sur la logique, et il exprime sa consternation à cette nouvelle dans sa réponse au philosophe britannique. Le second volume des Grundgesetze der Arithmetik était déjà chez l’imprimeur. Il ne sera publié que l’année suivante avec la note suivante :
« Pour un écrivain scientifique, il est peu d’infortunes pires que de voir l’une des fondations de son travail s’effondrer alors que celui-ci s’achève. C’est dans cette situation inconfortable que m’a mis une lettre de M. Bertrand Russell, alors que le présent volume allait paraître. »

Quand Poincaré ironise
Henri Poincaré voyait l’expérience et l’intuition comme les éléments essentiels pour fonder les mathématiques. Aussi était-il souvent ironique et même caustique envers ceux qui se gargarisaient de logique abstraite pour fonder l’arithmétique, en particulier Giuseppe Peano, Burali-Forti et le philosophe et logicien Louis Couturat, qui appartenait au même courant logiciste que Bertrand Russell. On peut lire dans Science et Méthode (Flammarion, 1908) : « Nous voyons d’abord M. Burali-Forti définir le nombre 1 de la manière suivante :
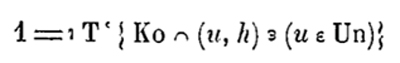
définition éminemment propre à donner une idée du nombre 1 aux personnes qui n’en auraient jamais entendu parler. J’entends trop mal le péanien pour oser risquer une critique, mais je crains que cette définition ne contienne une pétition de principe, attendu que j’aperçois 1 en chiffre dans le premier membre et Un en toutes lettres dans le second. »
« Je me hâte d’ajouter que la définition que M. Couturat donne du nombre 1 est plus satisfaisante. Un, dit-il en substance, est le nombre des éléments d’une classe dont deux éléments quelconques sont identiques. Elle est plus satisfaisante, dis-je, en ce sens que pour définir 1, il ne se sert pas du mot “un” ; en revanche, il se sert du mot “deux”. Mais j’ai peur que si on demandait à M. Couturat ce que c’est que “deux”, il ne soit obligé de se servir du mot “un”. »
Lire la suite