
Depuis le milieu des années 1980, Total a multiplié par 10 000 sa puissance de calcul avec le lancement de Pangea III en juin 2019, avec 25 pétaflops, soit 25 millions de milliards d’opérations par seconde (l’équivalent de cent trente mille ordinateurs portables), avec une capacité de stockage de 50 pétaoctets. Il est classé no 11 parmi les supercalculateurs les plus puissants au monde, public ou privé (TOP 500 de juin 2019) et no 7 parmi les plus efficaces énergétiquement (GREEN 500 de juin 2019). Cette puissance est obtenue en associant cinq cent cinquante-huit nœuds de calcul dotés chacun de deux CPU IBM Power9 de dix-huit cœurs (à 3,45 GHz) associés à six GPU NVIDIA Volta GV100.

Pangea III, le nouveau supercalculateur de Total.
Deux types de modélisation
Pour Total, historiquement, les calculs d’intérêt qui requièrent une puissance de calcul importante tournent autour de la modélisation des phénomènes physiques complexes. On peut citer par exemple l’imagerie de profondeur et la simulation réservoir, qui représentent 95 % de l’utilisation de Pangea III.
En imagerie de profondeur, on utilise les informations transmises par les ondes mécaniques pour cartographier en trois dimensions le sous-sol. Ces ondes, artificiellement produites, se propagent dans le sous-sol et reviennent à la surface, où elles sont enregistrées. En simulation réservoir, on essaye de prédire sur la durée, entre autres la production de pétrole ou de gaz de puits en simulant les écoulements et le transport des différents fluides dans les formations géologiques. Pour ces deux applications, on simule des modèles numériques très élaborés via le calcul haute performance.
On distingue deux types de modélisation.
La modélisation directe, qui nous intéresse ici, consiste à déterminer les inconnues y (t, x) fonctions du temps t et du positionnement dans l’espace x, pour un jeu de paramètres p (propriétés de la roche, position des puits ou bien de géophones, propriétés des fluides…), tels que M (y, p) = 0. Les inconnues y peuvent être par exemple la pression, la température, la vitesse du fluide, la vitesse sismique de l’onde…
Avec la modélisation inverse, on cherche les paramètres p* (souvent une petite partie des paramètres) qui minimisent la différence entre les inconnues y prédites par le modèle M et des valeurs observées yobs.
Solveurs et algorithmes
Le modèle M est constitué d’un système d’équations aux dérivées partielles (EDP) représentant la physique du problème. Dans les applications évoquées, il peut s’agir de l’équation de propagation des ondes, de la loi de conservation de masse ou bien de la loi de Darcy, qui exprime le débit d’un fluide à travers un milieu poreux en fonction de la différence de pression. Il n’existe pas de solution analytique à ces systèmes d’équations, on a donc généralement recours à des approximations numériques.
Lors de la première étape de l’approximation, on va mailler la géométrie d’intérêt en la découpant en plusieurs éléments. Dans la figure suivante, on peut voir (en haut) le maillage d’un réservoir pétrolier pour la simulation réservoir, et (en dessous) celui du sous-sol pour la propagation d’ondes. Les deux objets sont découpés en petits volumes que l’on nomme éléments. Les sommets des éléments sont les mailles.
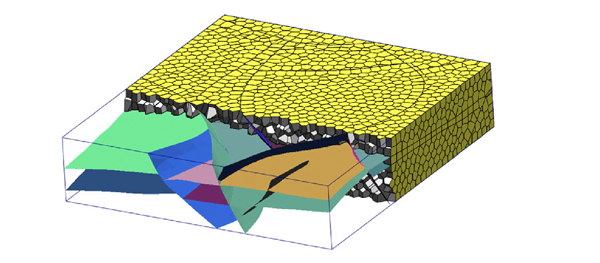
Maillage d’un réservoir de pétrole.
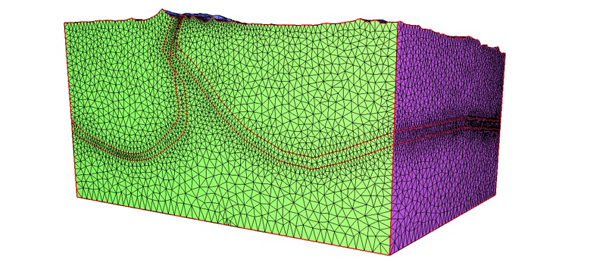
Maillage du sous-sol.
Dans une deuxième étape, les EDP seront discrétisées. Pour ce faire, les inconnues y – qui sont des variables continues dans l’espace et le temps – seront supposées constantes, sur chaque élément ou maille, et sur des périodes de temps, appelées les pas de temps.
Cette hypothèse va permettre d’obtenir une solution approchée mais résoluble du système d’EDP, et donc du modèle M, que l’on note M i ( y j , p j ) = 0, i étant le i ème pas de temps. Les inconnues et les paramètres sont maintenant des quantités discrètes définies sur chaque élément du maillage j. L’approximation M i du modèle M sera d’autant meilleure que les éléments du maillage et les pas de temps seront petits.
De nombreuses familles de méthodes de discrétisation existent : méthodes aux volumes finis, aux éléments finis, aux différences finies… La figure suivante illustre la méthode sur un maillage à une dimension.
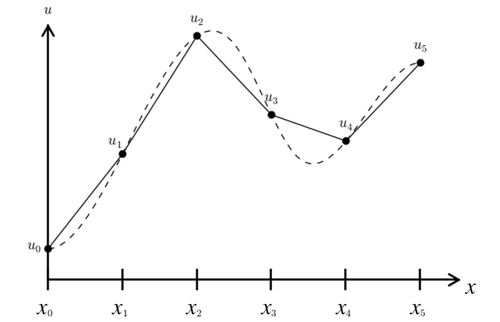
Exemple de discrétisation sur une fonction 1D.
La fonction continue à approximer est représentée par les traits en pointillé. Le trait plein montre l’approximation d’ordre 1 (approximation linéaire par morceaux), où la solution discrète n’existe qu’aux mailles.
Une fois discrétisé sur le maillage, le modèle M i est constitué d’un ensemble d’équations (linéaires ou non). Un solveur spécifique sera alors développé pour résoudre M i ( y j , p j ) = 0. Ce solveur est une succession d’algorithmes, en général constitué des étapes suivantes.
Pour un pas de temps i :
• calculer les paramètres pour chaque élément ou nœud du maillage ;
• assembler le système d’équations discrétisées ;
• résoudre M i ( y j , p j ) = 0 ;
- si le système d’équation est non linéaire, on utilise l’algorithme de Newton–Raphson
(voir FOCUS) ;
- si le système d’équation est linéaire, on le résout ;
• incrémenter i.
Les figures illustrent les résultats de simulations numériques à un pas de temps donné pour les deux applications mentionnées.

Résultats de la simulation d’écoulement dans un réservoir.
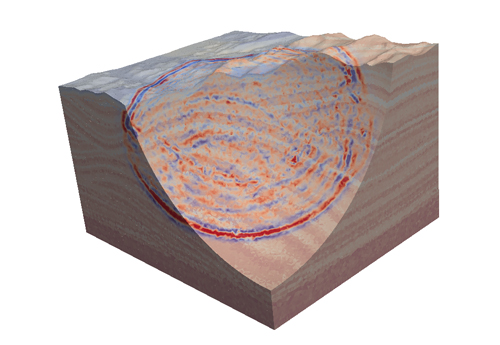
Résultats de la simulation de la propagation d’ondes.
Maintenant, comment construit-on un solveur qui tire profit du supercalculateur ? Un tel outil est constitué de nœuds de calcul, chaque nœud possédant une ou plusieurs unités de calcul (CPU ou GPU). L’idée est de répartir les tâches du solveur sur plusieurs nœuds.
Pour ce faire, on va partitionner le maillage en plusieurs domaines, comme illustré ci-dessous, et partager l’effort de calcul. Chaque couleur représente une partition. En général, le maillage est découpé en un nombre de partitions égal au nombre de nœuds de calcul.
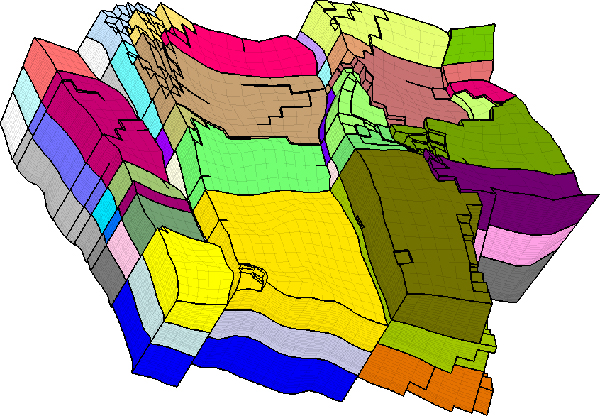
Exemple de maillage partitionné.
Communication et équilibre
Idéalement, on souhaiterait que plus on utilise de nœuds de calcul, plus le calcul soit rapide. Pour définir la mesure d’efficacité d’un solveur en parallèle, on utilise un anglicisme, la « scalabilité », qui mesure l’efficacité de l’algorithme à accroître ses performances au même rythme que celui de l’augmentation des ressources de calcul. La figure ci-contre en est un exemple : la ligne rouge montre une scalabilité parfaite théorique (où le temps de calcul est inversement proportionnel au nombre de nœuds de calcul). En pratique, les solveurs ont plutôt un comportement similaire à la courbe bleue, avec des performances qui se dégradent à partir d’un certain nombre de nœuds.
La dégradation de la scalabilité s’explique principalement par deux raisons : la surcharge de communication entre nœuds de calcul par rapport au calcul, et le déséquilibrage de la charge de calcul.
La « communication » définit l’échange d’information entre les différentes partitions de calcul. En effet, les différents calculs – que ce soit les calculs de propriétés, l’algorithme de Newton–Raphson ou bien la résolution du système linéaire – ne peuvent pas être isolés sur une seule et même partition et nécessitent des échanges d’information entre ces différentes partitions. Pour limiter cet effet, on peut doubler certains éléments du maillage, comme indiqué sur la figure ci-dessous ; ces éléments sont appelés les éléments fantômes. Certains calculs seront dupliqués sur ces éléments, ce qui ajoute un surcoût de calcul. Lorsque les partitions deviennent trop petites – nombre d’éléments fantômes trop important par rapport aux non fantômes –, ce surcoût pénalise trop fortement les gains de parallélisme. Aussi, d’autres opérations comme les produits « matrice vecteur » sont globales et nécessitent des échanges entre les partitions. Tous ces échanges sont nommés communications. Concrètement, ils représentent des échanges de données entre les nœuds de calculs.
.jpg)
Représentation du maillage et ses cellules fantômes sur plusieurs partitions.
Le déséquilibre de la charge de calcul intervient lorsqu’une partition fait beaucoup plus de travail que les autres. Comme ces partitions ne sont pas indépendantes et communiquent, la plus lente pénalise l’ensemble. Il faut donc définir les partitions et la stratégie de calcul de manière à équilibrer la charge.
Les méthodes d’ensemble
Certains paramètres p du modèle M(y, p) = 0 sont incertains, principalement à cause de la nature du sous-sol, qui ne peut être précisément déterminée pour la modélisation directe. Pour capturer cette incertitude, on adopte une approche probabiliste de type méthode d’ensemble. Chaque paramètre est caractérisé par une densité de probabilité.
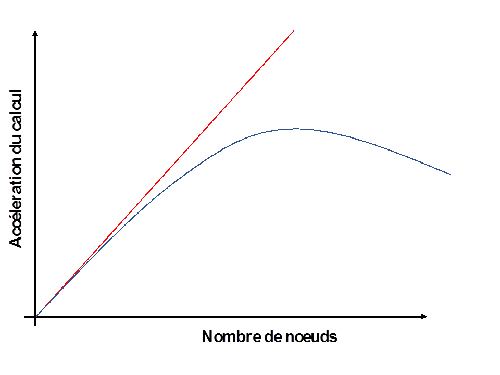
Exemple de courbes de « scalabilité ».
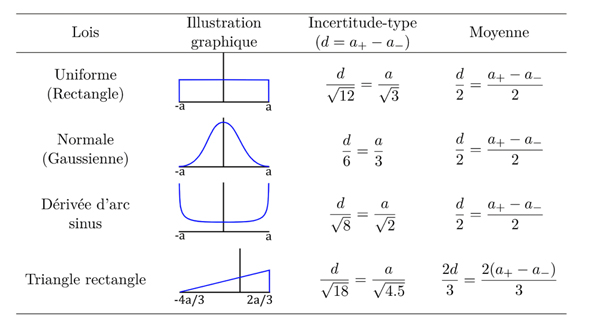
Types de lois de densité de probabilité pour les paramètres incertains.
Un algorithme de type Monte-Carlo est utilisé pour capturer l’impact des paramètres incertains sur une réponse. Cet algorithme consiste à appeler, à de multiples reprises, le modèle discrétisé Mi( yj , pj ) = 0 où l’on fait varier la valeur des paramètres incertains pj .
Un appel est nommé réalisation. Chaque réalisation fera appel à une combinaison de paramètres incertains respectant les densités de probabilité. Au final, la réponse est échantillonnée, les résultats sont similaires à ceux de la figure ci-contre.
On constate qu’il faut un nombre important de réalisations pour capturer la moyenne et les moments d’ordre supérieur (comme la variance).
Ici, le calcul haute performance est d’une grande aide ! L’algorithme de Monte-Carlo a une scalabilité parfaite car chaque réalisation est indépendante des autres, il n’y a aucun problème de communication ou bien d’équilibrage de charge.
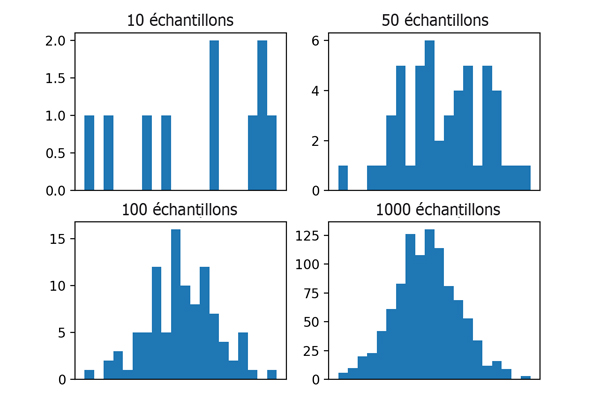
Exemples de résultats d’échantillonnage par méthode de Monte-Carlo.
Le calcul haute performance est un atout majeur pour la modélisation de procédés physiques complexes. Il peut être utilisé pour la résolution du problème direct avec un effort particulier sur les algorithmes pour profiter au mieux du calcul en parallèle, mais aussi lors de l’utilisation d’algorithmes de type Monte-Carlo. La modélisation inverse, qui nécessite de réaliser un certain nombre de modélisations directes, tire donc également parti des gains obtenus par l’utilisation du calcul haute performance. Cependant, d’autres efforts, liés aux algorithmes d’optimisation et aux problèmes inverses, sont nécessaires pour obtenir le meilleur des supercalculateurs.
Alexandre Lapene et Philippe Cordier sont respectivement adjoint au Directeur et Directeur du programme de recherche « Calcul scientifique, science des données et intelligence artificielle » chez Total.
Lire la suite