
Confortablement installés dans vos sièges, vous attendez impatiemment le décollage, avec quand même une petite appréhension au creux de l’estomac. Vous vous émerveillez devant la prouesse technologique qui va permettre à cette machine de plusieurs centaines de tonnes de tenir en l’air comme par magie et de se déplacer à plus de 800 km/h. Mais vous êtes probablement loin de vous douter de la quantité de calculs extrêmement sophistiqués que le constructeur de l’avion, la compagnie aérienne et le pilote ont dû réaliser avant même l’embarquement…
Quelques problèmes sont déjà à résoudre avant de décoller. L’un des premiers soucis de l’équipage est bien sûr d’embarquer, dans les réservoirs, la juste quantité de carburant nécessaire à l’accomplissement de la mission. Trop, on alourdit inutilement l’avion, ce qui est pénalisant en termes de consommation de kérosène. Pas assez, on devine les conséquences.
Un autre point important est de s’assurer que l’avion pourra effectivement réaliser sa mission, et en particulier que la longueur de la piste est suffisante pour permettre le décollage, que les obstacles que l’on va rencontrer en cours de route (l’immeuble qui se trouve au bout de la piste, la montagne qu’il va bien falloir passer…) pourront être survolés sans encombre, ou encore que l’on pourra toujours trouver un aéroport accessible vers lequel se dérouter en cas de défaillance survenant en cours de route. Il existe ainsi tout un ensemble d’exigences définies par la réglementation aéronautique qui sont liées à la performance de l’avion, elle-même intimement liée à sa trajectoire.
Calculer la trajectoire
Afin de pouvoir répondre à toutes ces questions, il faut donc d’abord calculer la trajectoire, que l’on doit ici entendre au sens large ; on peut parler d’« évolution au cours du temps des paramètres représentatifs de la performance l’avion ». La position (latitude δ, longitude λ, altitude z), la masse m de l’appareil (qui diminue au cours du vol au fur et à mesure que le carburant est consommé), sa vitesse v, la poussée T sont de tels paramètres. Certains sont imposés par le pilote, qui va garder constantes l’altitude et la vitesse en croisière, alors qu’en montée il imposera plutôt la poussée et la vitesse (en descente, ce sont la pente et la poussée qui seront fixées). Les paramètres dont la valeur est directement imposée par le pilote sont les variables de contrôle ou variables de commande (notées u), les autres sont les variables d’état (notées x).
Pour calculer la trajectoire, les modèles mathématiques de la physique fournissent un ensemble d’équations qui décrivent comment évoluent les variables d’état avec le temps. Par exemple, le modèle de consommation des moteurs renseigne sur le débit de carburant
La valeur de x à un instant t quelconque s’obtient alors par intégration de cette équation entre un instant initial t0 , pour lequel on connaît l’état de l’avion (au décollage par exemple, où l’on connaît bien sûr la masse, la vitesse – qui est nulle –, ainsi que la position et l’altitude du seuil de piste), et l’instant courant t :
Le calcul de cette intégrale est réalisé par des méthodes numériques, comme par exemple une méthode de Runge–Kutta.

Doser son modèle
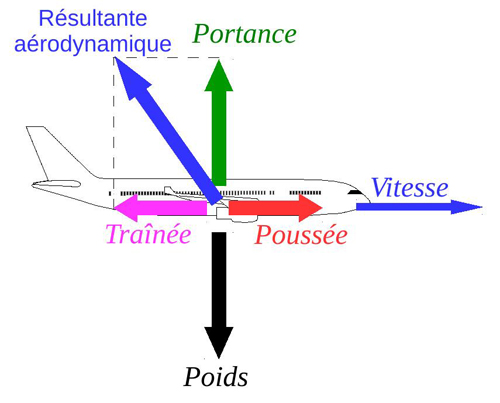
La fonction f , qui décrit comment varie le vecteur d’état, représente la physique des phénomènes qui entrent en jeu au cours du vol : elle constitue un modèle mathématique de la dynamique de l’avion, et est elle-même composée de plusieurs sous-modèles représentant les forces aérodynamiques (portance et traînée), la force de propulsion (poussée), la force de gravité (poids) ou encore la consommation de carburant. Ces modèles sont établis par le constructeur de l’avion.
Généralement, plus un modèle est représentatif, plus il est sophistiqué et il peut alors s’avérer nécessaire de le simplifier pour pouvoir l’utiliser pratiquement. C’est le cas en particulier pour les forces aérodynamiques, qui sont la conséquence du mouvement de l’air autour de l’avion et dont le modèle le plus complet est constitué par un ensemble d’équations aux dérivées partielles, les fameuses équations de Navier–Stokes : leur résolution est loin d’être évidente (et en tout état de cause inenvisageable au sein d’un algorithme d’intégration de trajectoire avec les moyens actuels, et en particulier par un calculateur embarqué à bord). On choisit alors d’introduire des hypothèses simplificatrices (pas de viscosité, fluide incompressible…), qui conduisent à des équations certes simplifiées mais qui traduisent l’essentiel du phénomène à modéliser. Par exemple, le modèle théorique (simplifié) de la ligne portante de Prandtl nous apprend que les coefficients Cx et Cz , qui représentent respectivement les forces de portance et de traînée (sans dimension), sont liés par une relation de la forme
Mais il arrive que l’on ne dispose d’aucune information théorique sur la fonction à modéliser ! Dans ce cas, on construit un modèle totalement empirique et la difficulté est alors de savoir quelles sont les principales variables dont il dépend et quelle est la nature de la fonction qui relie ces variables à la grandeur à modéliser. Pour cela, on s’appuie sur l’analyse de résultats d’essais qui peuvent être numériques (calculs réalisés avec le modèle complet lorsque celui-ci existe), ou réalisés au sol (soufflerie, banc moteur), ou encore en vol.
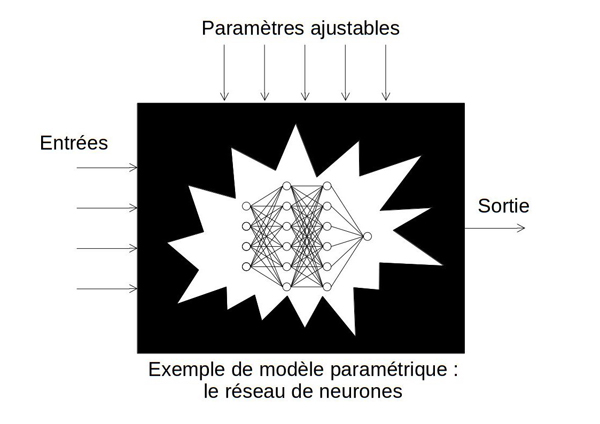
Parfois, l’analyse statistique de ces résultats fait apparaître des relations simples (linéaires, typiquement) entre les variables d’entrée et de sortie du modèle. La plupart du temps cependant, cette relation est très élaborée et on va alors modéliser cette dépendance par des fonctions paramétriques dont les capacités de représentation sont suffisamment importantes : il peut s’agir de tables de valeurs numériques dans lesquelles on va aller interpoler, de polynômes, ou encore de réseaux de neurones. Le choix de l’un ou l’autre de ces modèles résulte d’un compromis entre la capacité de représentation (la précision du modèle) et le nombre de paramètres ajustables (les valeurs de la table dans le cas d’un modèle tabulé, les coefficients pour un polynôme ou les poids et seuils pour un réseau de neurones), et donc la taille qu’ils occupent dans la mémoire de l’ordinateur, le temps de calcul, l’interprétation physique de ses paramètres…
Une fois choisie la structure du modèle, il faut déterminer la valeur de ses paramètres. Pour cela on s’appuie sur un ensemble de points en lesquels on connaît la valeur de la fonction à modéliser ; on parle alors d’identification. Ces points sont en nombre limité : les essais (au sol ou en vol) sont chers et les calculs numériques sont coûteux en temps. Il faut au moins autant de points (sensiblement plus, dans la pratique) que de paramètres à ajuster. L’identification de ces derniers peut alors être effectuée par une méthode des moindres carrés.
La délicate phase d’optimisation
Grâce aux modèles de l’avion et aux méthodes d’intégration numériques qui les mettent en œuvre, on est maintenant capable de calculer la trajectoire de vol qui correspond à des actions de pilotage données. Pourquoi alors s’arrêter en si bon chemin ? On peut en effet à ce stade envisager de trouver la commande u qui conduit à « la meilleure » trajectoire.
Pour cela, il faut d’abord définir ce que l’on entend par « meilleure trajectoire » : est-ce celle qui consomme le moins de carburant ? Celle qui arrive le plus tôt à destination ? Celle qui fatigue le moins l’avion ? Celle qui émet le moins de particules polluantes ? Ou encore celle qui fait le moins de bruit à proximité des habitations ? Ces différents critères sont généralement antagonistes ! Réduire le temps de vol se traduit ainsi par une augmentation de la consommation de carburant.
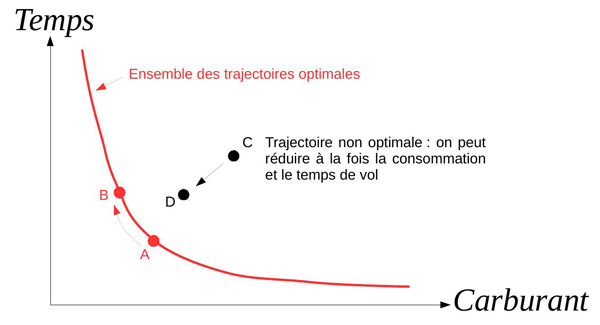
On fait face à un problème d’optimisation multicritère. Ce genre de situation n’a généralement pas une solution unique mais un ensemble de « solutions équivalentes » en ce sens qu’on ne peut pas en trouver de « meilleures » (qui amélioreraient simultanément tous les critères). Ces options constituent un front de Pareto. Par exemple, si l’on ne considère que le temps et la consommation de carburant, les solutions ont l’allure représentée sur la figure ci-dessous. Ce type de problème d’optimisation est difficile à résoudre et coûteux en temps de calcul. Heureusement, il existe un critère plus général qui réconcilie tout le monde : le coût global de la mission. Ainsi, si l’on sait attribuer un coût (exprimé dans une même unité) à chacun des critères, on peut se ramener à un problème d’optimisation plus classique pour lequel il s’agit de minimiser un seul critère ϕ (u) et qui admet en général une solution unique bien définie.
Les commandes u (t) que l’on cherche à déterminer sont des fonctions du temps : il s’agit donc d’un problème de contrôle optimal, généralement difficile à résoudre par les techniques classiques (principe du maximum de Pontriaguine, équations de Hamilton–Jacobi–Bellman). On va alors le simplifier en fixant a priori la forme des commandes en question, c’est-à-dire en restreignant l’espace de recherche à un ensemble de fonctions particulières paramétrées par un petit nombre de variables. Ce choix est justifié par la nécessité de fournir à l’équipage une consigne de pilotage simple et intelligible (une vitesse, une altitude ou une poussée constante…). On « découpe » alors la trajectoire en différentes phases (montée, croisière, descente) sur chacune desquelles on impose à la commande de rester constante.
Encore faut-il que cette trajectoire soit réalisable ! Plusieurs contraintes sont à prendre en compte. Certaines sont liées aux capacités de l’avion (la vitesse ne doit pas être trop faible sinon la force aérodynamique de portance n’arrive plus à équilibrer le poids et c’est le décrochage ; inversement, la poussée des moteurs étant limitée, la vitesse ne pourra pas dépasser une certaine valeur). D’autres sont imposées par la réglementation aéronautique et par le contrôle aérien. L’ensemble des paramètres de la trajectoire et de la commande sont ainsi astreints à vérifier un ensemble de conditions que l’on peut toujours mettre sous la forme g (x, u) ≤ 0. Finalement, le problème s’écrit : trouver u [ ℝn tel que ϕ (u) soit minimum, tout en respectant la contrainte g (x, u) ≤ 0. Il s’agit d’un problème classique d’optimisation sous contraintes.

Des géodésiques et des graphes
Un cas particulier intéressant concerne l’optimisation du profil latéral de la trajectoire (sa projection sur la surface terrestre). En l’absence de contrainte particulière, la route qui minimise la distance entre deux points du globe est une géodésique. Si l’on assimile la Terre à une sphère, il s’agit d’un arc de grand cercle *. Mais la route la plus courte n’est pas toujours la plus économique : suivant les conditions météorologiques rencontrées, en particulier le vent, il peut être intéressant de s’en écarter. Les navigateurs le savent bien !
(* Sur une surface sphérique, une géodésique, appelée aussi grand cercle, est définie par l’intersection de la sphère avec un plan passant par son centre.)
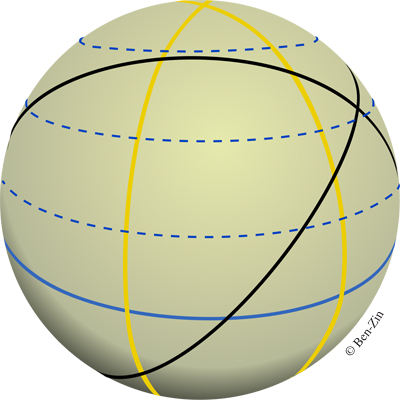
Cinq grands cercles (en traits pleins) sur la sphère.
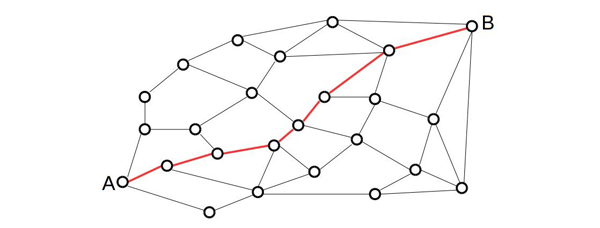
Par ailleurs, dans de nombreuses zones du globe, le choix de la route n’est pas libre : elle doit passer par des points appartenant à un réseau de balises implantées au sol. La détermination de la route « optimale » se ramène alors à un problème de plus court chemin dans un graphe. Le coût de chaque arrête dépend de la consommation de carburant, qui dépend elle-même de la masse de l’avion au début de cette arrête (plus il est lourd, plus il consomme) et du vent que l’on va y rencontrer (la consommation augmente avec le vent de face), lequel varie en fonction du temps : il s’agit donc d’un graphe pour lequel les coûts des arêtes ne sont pas fixes mais dépendent du chemin suivi pour y arriver.
Enfin, la route doit aussi satisfaire une contrainte liée à la sécurité : il faut en effet qu’en chaque point l’avion dispose de suffisamment de carburant pour pouvoir rejoindre un aéroport de déroutement en cas de défaillance conduisant à une augmentation notable de la consommation de carburant (perte d’un moteur par exemple). Ces différentes caractéristiques rendent le problème bien différent de celui du classique plus court chemin proposé par tous les GPS qui équipent les automobiles !
On le constate, les mathématiques constituent un outil de choix pour modéliser le comportement des avions et pour en optimiser l’utilisation opérationnelle, donc la prise de décision. Ces aspects se retrouvent naturellement à plusieurs niveaux, qu’il s’agisse de définir l’architecture de l’appareil (nombre de moteurs, géométrie des ailes…) ou de permettre aux compagnies aériennes de rentabiliser leur exploitation. L’optimisation de la production, quant à elle, soulève des problèmes d’ordonnancement de tâches. L’analyse de sécurité fait pour sa part intervenir les probabilités et les statistiques. Galilée affirmait que la nature s’écrit en langage mathématique : c’est aussi le cas pour bon nombre de problèmes dans l’industrie aéronautique !
Serge Laporte est ingénieur en aéronautique et enseignant-chercheur.
Lire la suite