Méthode du gradient : skier pour minimiser

À chaque point (x, y) du plan, on associe naturellement une « altitude » z, fonction de x et de y, que l’on notera aussi  f (x, y). La visualisation en trois dimensions des points de coordonnées (x, y, f (x, y)) produit quelque chose qui peut ressembler à une piste de ski.

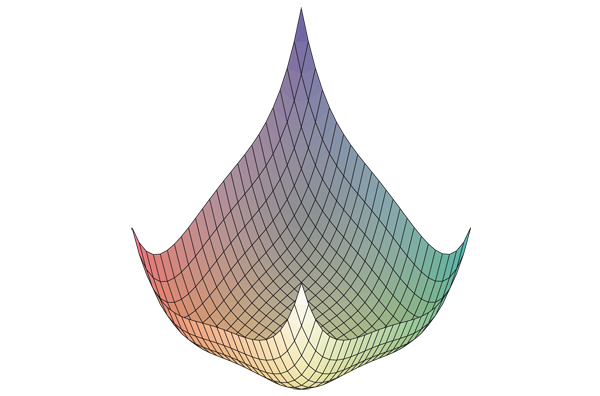
Graphe de la fonction qui au nombre x associe f ( x, y ) =x ⁴ + y ⁴– 2( x – y ) ².

Dans l’exemple du schéma, il est apparent qu’il y a un point quelque part qui se trouve plus bas que tous les autres. C’est celui-là que le skieur fatigué par une longue journée sportive voudrait trouver. Mathématiquement, il s’agit de déterminer les valeurs de x et de y pour lesquelles l’altitude, f (x, y), est minimale. Comment le localiser ?

L’art de l’approximation

Une idée consiste à partir d’un point quelconque (x, y) du plan, puis d’examiner les valeurs de f aux points qui l’entourent, à savoir les points de coordonnées (x + h, y + k), où les valeurs de h et de k sont supposées « suffisamment proches » de 0. Dans ces hypothèses, on dispose de l’approximation suivante :

\( f (x+h,\,y+k)\simeq f (x, y)+ h \,\partial f / \partial x + k \, \partial f / \partial y.\)

Les expressions ∂f / ∂x et ∂f / ∂y sont les dérivées partielles de  f , c’est-à-dire des valeurs exprimant la variation de  f dans la direction de l’axe des abscisses (pour la première) et des ordonnées (pour la seconde). Il s’agit de valeurs qui ne dépendent que du point (x, y) choisi, et qui se calculent par des méthodes d’analyse classique.

Avec les deux valeurs ∂f / ∂x et ∂f / ∂y, on forme un vecteur à deux composantes, que l’on appelle le gradient de  f au point (x, y). Dans l’approximation, on peut remarquer que la partie h ∂f / ∂x + k ∂f / ∂y s’interprète comme le produit scalaire du gradient avec le vecteur \( \vec {v}\) de composantes h et k :

\( \overrightarrow{v} . \overrightarrow{\text{grad}} (f) = \begin{pmatrix} h \\ k \end{pmatrix} . \begin{pmatrix} \partial f/ \partial x \\ \partial f/ \partial y \end{pmatrix} = h \dfrac{\partial f}{\partial x} + k \dfrac{\partial f}{\partial y} .\)

À norme fixée, le choix de \( \vec {v}\) qui minimise ce produit scalaire consiste à prendre \( \vec {v}\) dans la direction opposée à celle du gradient. Il s’agit de la direction de plus grande pente, celle qui, à l’endroit (x, y) où se trouve le skieur, l’assure au moins au début de descendre « le plus possible ». Se diriger dans cette direction est donc un choix raisonnable, en l’absence d’information globale à cause de la brume…

On peut alors recommencer la même opération en partant du nouveau point atteint. Il sera possible d’avancer tant que les dérivées partielles ne sont pas toutes les deux nulles. Là où elles sont toutes les deux nulles, on parle de point critique : ce sont les seuls points où le skieur est susceptible d’avoir atteint le minimum convoité.

Dans le cas particulier de la surface considérée, on trouve trois points critiques :

\( (0, 0), (\sqrt{2}, -\sqrt{2}) \,\text{et} \,(-\sqrt{2}, \sqrt{2}).\)

Les valeurs de  f en ces points sont 0 et –8. Donc, s’il existe un minimum de  f sur le plan, c’est la valeur –8 < 0, qui est atteinte en \( (\sqrt{2}, -\sqrt{2})\)  et aussi en  \( (-\sqrt{2}, \sqrt{2}).\)

En toute rigueur, ces calculs ne démontrent pas l’existence d’un minimum : on a seulement établi que si celui-ci existe, alors c’est en ces points qu’on l’atteindra. Pour démontrer l’existence effective d’un minimum, une méthode consiste à utiliser la notion topologique de compacité (voir FOCUS). Avec cet outil, on a effectivement établi que, quels que soient x et y, on a x ⁴ + y ⁴ – 2(x – y) ² ≥ –8. Voilà ainsi une inégalité algébrique obtenue en n’utilisant que des outils d’analyse !

La ligne de plus grande pente

Exploitons l’approximation obtenue pour  f aux points qui entourent un point donné. La méthode du gradient consiste, à partir d’un point initial fixé M₀ = ( x₀, y₀), à construire une suite de points M₁, M₂, M₃… M _n… par récurrence, où chaque nouveau point s’obtient en se déplaçant d’un pas (de taille fixée une fois pour toutes, et suffisamment petite) dans la direction de plus grande pente.

Il est également nécessaire de définir un test d’arrêt. Pour cela, on se donne un nombre ε > 0, et l’on s’arrête lorsque la norme du gradient en M_n est plus petite que cette précision ε, ce qui traduit le fait que la pente, bien que maximale à cet endroit, est devenue « suffisamment faible » pour qu’on puisse considérer que l’on est à l’horizontale.

L’analogie avec la descente à ski montre que les cas d’échecs de l’algorithme sont nombreux. En particulier, la descente peut aboutir à un minimum local, c’est-à-dire à un creux localisé qui n’est pas l’altitude la plus basse du point de vue global. Pour éviter ce type de problème, une visualisation de la surface avec un logiciel peut aider. 

Par exemple, la méthode du gradient n’est pas adaptée pour optimiser la fonction g définie par g (x, y) = sin (x ² – y ²) cos (2x + y + 1), puisque son dessin est rempli de « bosses ».

Selon le point de départ, la méthode du gradient donnera dans ce cas des résultats différents. Cependant le maximum et le minimum de g sont faciles à déterminer. En effet, comme il s’agit du produit de deux fonctions comprises entre –1 et 1, les candidats naturels comme optimums sont –1 et 1. On vérifie que c’est bien le cas en trouvant des points où ils sont atteints. On sort alors de la méthode du gradient, pour entrer dans celle de la résolution des systèmes d’équations.

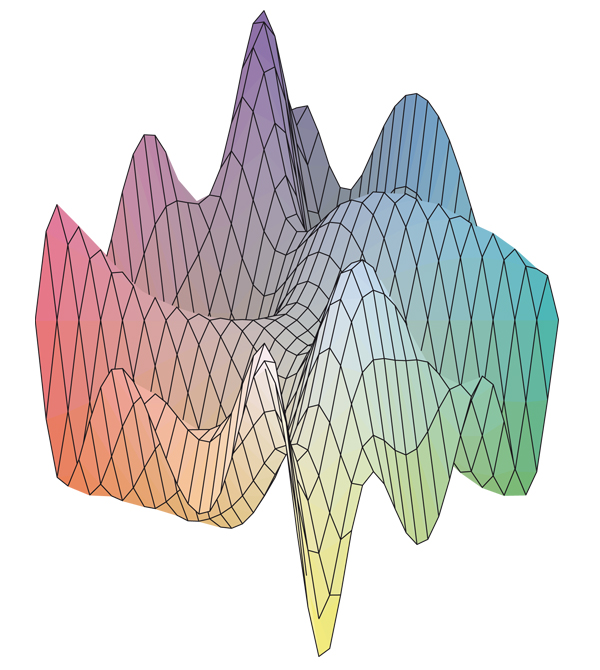
Représentation de la fonction g qui à x associe sin( x ²– y ²) × cos( 2x + y + 1 ).

[encadre]

De l'existence d'un minimum

Sur un disque fermé, toute fonction continue admet un minimum et un maximum. Ce fameux théorème s’applique plus généralement aux fonctions continues sur les compacts, c’est-à-dire les ensembles fermés et bornés.

Pour pouvoir utiliser ce résultat dans le cas de notre fonction particulière f (qui est définie sur le plan tout entier et non sur un disque), il suffit de montrer que la recherche du minimum de  f peut être restreinte aux points (x, y) à l’intérieur d’un certain disque. Il est suffisant pour cela de montrer que, pour un rayon R « assez grand », et pour tout point (x, y) hors du disque de centre (0, 0) et de rayon R, on a  f (x, y) > 0 (et donc qu’aucun point hors de ce disque ne fournit le minimum cherché, puisque l’on sait déjà que  f peut prendre des valeurs négatives).

Passons donc en coordonnées polaires, en écrivant x = r cos θ et y = r sin θ. Il vient alors :

f (x, y) = r ² [r ²(cos⁴θ + sin⁴θ ) – 2(cosθ – sinθ ) ²].

Un petit raisonnement de trigonométrie, de calcul différentiel ou de compacité permet de se convaincre qu’il existe a > 0 tel que cos⁴θ + sin⁴θ ≥ a pour tout θ, et donc que f (x, y) ≥ r ²(a r ² – 8).

Cette inégalité conduit au résultat cherché.

[/encadre]