La programmation linéaire

La programmation linéaire est née dans les années 1930 des travaux de l’économiste et mathématicien soviétique Leonid Vitalievitch Kantorovitch (1912–1986), qui reste le seul chercheur soviétique ayant reçu à ce jour le « prix Nobel » d’économie, en 1975.

Dans un processus de décision, on est souvent amené à devoir choisir, parmi un ensemble de solutions possibles, celle qui va rendre optimale une certaine fonction f de variables assujetties à des contraintes. Par exemple, on cherche à rendre maximal un rendement de production en présence de ressources limitées, ou à payer un coût minimal pour un achat d’une qualité satisfaisante, ou encore à composer un mélange de qualité dont le prix de revient soit minimal.

En pratique, et tout spécialement dans les applications économiques, des problèmes concrets se traduisent donc mathématiquement par l’optimisation (maximisation ou minimisation) d’une fonction f dont les variables, notées x₁, x₂… x_n , doivent satisfaire des contraintes définissant un ensemble E situé dans l’espace numérique à n dimensions (voir Mathématiques et économie. Bibliothèque Tangente 62, 2018).

Des effets proportionnels aux causes

Un cas particulier, fréquent en pratique, est celui où la fonction à étudier est linéaire, c’est-à-dire du premier degré en toutes ses variables. Dans cette situation, les effets sont proportionnels aux causes et additifs. Il en va ainsi des quantités fabriquées d’un produit : elles sont proportionnelles aux quantités de matières premières utilisées et les productions de deux (ou plusieurs) ateliers fabriquant le même article s’ajoutent entre elles. Mathématiquement, la fonction considérée f est alors de la forme :

\( f(x_1,x_2\ldots x_n ) = \sum_{i=1}^{n}c_ix_i\)

où les coefficients c_i sont des constantes. Cette fonction f> est appelée l’objectif, c’est elle qu’il s’agit d’optimiser.

L’ensemble E sur lequel la fonction f doit être optimisée est, quant à lui, déterminé par des contraintes linéaires imposées aux variables. Il s’agit donc uniquement d’inégalités ou égalités faisant intervenir les variables x_i au premier degré. Ces variables ont le plus souvent une signification concrète ou matérielle (quantités, durées, valeurs monétaires…) qui les oblige à être positives ou nulles. Les contraintes sont dès lors de deux types : d’une part, les conditions de non-négativité (à savoir x_i ≥ 0 pour tout i compris entre 1 et n) ; d’autre part, les vraies contraintes (c’est-à-dire celles qui sont spécifiques à la situation étudiée, et qui doivent donc être précisées dans chaque cas particulier). Quitte à modifier la présentation de vraies contraintes par des opérations algébriques élémentaires, l’ensemble E des programmes réalisables peut s’écrire sous la forme suivante :

\( E=\big\{(x_1,x_2\ldots x_n ) \vert ~\hbox{pour}~ 1\leq i\leq n,x_i\leq 0,\, \sum_{j=1}^{m}a_{ij}x_j\leq b_i\big\}.\)

Les valeurs attribuées aux variables x_i sont souvent appelées activités. Elles traduisent généralement une décision prise par l’organisme qui pose le problème. C’est pourquoi les éléments de l’ensemble E sont quant à eux souvent nommés des programmes réalisables.

Le panier du consommateur

L’exemple le plus élémentaire est lorsque n = 2 (on a deux variables, notées ici x et y plutôt que x₁ et x₂). Il concerne un consommateur qui achète deux produits X et Y en quantités x et y et à des prix unitaires de (mettons) 3 euros et 2 euros respectivement ; il en retire une satisfaction U (on parle techniquement d’utilité) mesurée par une expression de la forme U = 4x + 5y ; il dispose enfin à cet effet d’un budget maximum de 600 euros. La question posée consiste à déterminer la combinaison (on dit dans le jargon le panier) de biens qu’il doit acquérir pour avoir la plus grande satisfaction possible.

Mathématiquement, cette personne cherche à maximiser la fonction f donnée par f (x, y) = 4x + 5y sous les conditions de non-négativité et la (vraie) contrainte budgétaire, soit sur l’ensemble E défini par les inégalités suivantes : x ≥ 0, y ≥ 0, 3x + 2y ≤ 600.

Dans le plan euclidien, l’ensemble des programmes réalisables E est le triangle ayant pour sommets les trois points P₁(0, 300), P₂(200, 0) et P₃(0, 0).

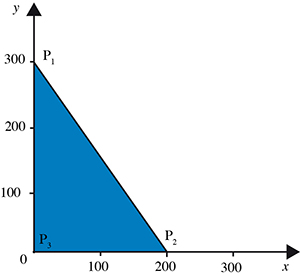
L’ensemble des programmes réalisables est le triangle coloré.

Généralement, pour trouver un éventuel maximum d’une fonction f à deux variables x et y, on commence par en annuler les deux dérivées partielles. Mais la linéarité de l’objectif rend cette méthode inefficace puisque la première dérivée partielle (par rapport à x) donne la constante 4 et la seconde (par rapport à y) vaut identiquement 5. En fait, il n’existe aucun maximum local de f dans l’intérieur de E (c’est-à-dire dans le triangle dont on exclut les trois côtés).

Pourtant, d’après un théorème dû à Karl Weierstrass, le maximum (global, ce que l’on cherche) de f sur E existe puisque la fonction f est continue et que E est un ensemble compact (c’est-à-dire fermé et borné). Le maximum en question ne peut donc être atteint que sur le bord (techniquement, la frontière) de E, c’est-à-dire sur l’un des trois segments de droite S₁, S₂ et S₃ reliant respectivement P₁ à P₂, P₂ à P₃ et P₁ à P₃.

Sur S₁, on dispose de l’égalité issue de la vraie contrainte, à savoir 3x + 2y = 600. En conséquence, sur ce segment, l’objectif peut ne dépendre plus que de la seule variable x. Il s’agit dès lors de maximiser la fonction :

g₁(x) = 4x + 5 (300 – 3x / 2) = –7x / 2 + 1 500

lorsque x parcourt l’intervalle [0, 200]. Cette fonction g₁ est affine, donc sa dérivée (identiquement égale à – 2) ne s’annule pas. Le maximum de g₁ sur l’intervalle en question est donc atteint (toujours en vertu du théorème de Weierstrass) en l’une de ses deux extrémités, x = 0 (avec y = 300) ou x = 200 (avec y = 0).

Sur S₂, inclus dans l’axe horizontal du plan, on a y = 0, de sorte que l’objectif s’écrit dans ce cas g₂(x) = 4x ; il convient de l’étudier lorsque x varie encore dans [0, 200]. À nouveau, on trouve que le maximum cherché est atteint en une extrémité de l’intervalle considéré : soit en x = 0 (avec y = 0), soit en x = 200 (avec y = 0).

Sur S₃, situé sur l’axe vertical, on a x = 0, de sorte que l’objectif s’écrit cette fois sous la forme g₃(y) = 5y, la variable y pouvant alors parcourir l’intervalle [0, 300]. Comme précédemment, le maximum cherché est atteint en une extrémité de l’intervalle en question, donc en y = 0 (avec x = 0) ou en y = 300 (avec x = 0).

Au total, le maximum de f sur E est nécessairement atteint en l’un des sommets P₁, P₂ ou P₃ du triangle des programmes réalisables. Comme f (0, 300) = 1 500, f (200, 0) = 800 et f (0, 0) = 0, le maximum de f vaut 1 500 et est atteint au sommet P₁. Concrètement, le consommateur doit acheter uniquement le produit Y, en quantité de 300 unités.

Cette solution peut être facilement vérifiée géométriquement. En effet, parmi toutes les droites parallèles d’équation 4x + 5y = k (où k désigne une constante), celle qui touche l’ensemble E (afin de vérifier simultanément les trois contraintes) en étant située « le plus haut » dans le plan (puisque l’on recherche un maximum) est celle qui rencontre le sommet P₁ (avec donc k = 1 500).

Rencontre aux sommets

Dans le cas général, il s’agit d’optimiser (maximiser ou minimiser) une fonction linéaire à n variables sur un ensemble E des programmes réalisables déterminé par les n conditions de non-négativité et par m vraies contraintes. Cet ensemble E est, dans l’espace à n dimensions, un polyèdre convexe (voir FOCUS).
Comme dans le cas de deux variables, f ne possède aucun optimum local en un point intérieur de E puisque ses dérivées partielles ne s’annulent pas toutes simultanément (à moins que f = 0, mais alors il n’y a pas de problème d’optimisation à résoudre). Grâce au théorème de Weierstrass, un éventuel extremum est donc atteint sur la frontière de E, c’est-à-dire au sein d’une « face » de E ; or, chaque face est un nouveau polyèdre de dimension moindre, de sorte que le même raisonnement peut être recommencé. En répétant autant de fois que nécessaire cet argument (à savoir au plus n fois), on arrive finalement à la conclusion que l’extremum cherché, s’il existe (ce qui est le cas lorsque E est borné), est nécessairement atteint en un point extrême de E. Il suffit donc de rechercher tous ces derniers (voir FOCUS), puis de conserver la plus grande (pour un maximum) ou la plus petite (pour un minimum) valeur prise par l’objectif en ces points.
Cette méthode s’applique en théorie dans tous les cas, mais elle devient vite impraticable, notamment lorsque le nombre de variables est élevé (et il n’est pas rare que des problèmes avec des dizaines, voire des centaines de variables soient rencontrés dans des situations réelles). C’est pourquoi ont été développées des techniques spécifiques de résolution telles que l’algorithme du simplexe (voir les Algorithmes, Bibliothèque Tangente 37, 2014), mis au point par le mathématicien américain George Bernard Dantzig (1914–2005).

En guise d’illustration, recherchons le minimum de la fonction :
h (x₁, x₂, x₃, x₄) = x₁ – 2x₂ + 3x₃ – 4x₄,
sous les contraintes x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0, x₄ ≥ 0, x₁ + x₂ + x₃ + x₄ ≤ 1, 2x₁ ≤ 1.
L’ensemble H des programmes réalisables est un polyèdre convexe dans l’espace à quatre dimensions ; il est visiblement borné (au vu des vraies contraintes). L’extremum recherché, dont l’existence est garantie par l’inoxydable théorème de Weierstrass, est atteint en un point extrême de H.
Parmi les quinze sous-systèmes de quatre équations formés à partir des six égalités x₁ = 0, x₂ = 0, x₃ = 0, x₄ = 0, x₁ + x₂ + x₃ + x₄ = 1, 2x₁ = 1, seuls huit d’entre eux donnent un point extrême, car les sept autres ne sont pas « de type Cramér » ou bien livrent des solutions qui n’appartiennent pas à H. Les points extrêmes de H sont donc les suivants : (0, 0, 0, 0), (0, 0, 0, 1), (0, 1, 0, 0), (0, 0, 1, 0), (1/2, 0, 0, 0), (1/2, 0, 0, 1/2), (1/2, 0, 1/2, 0) et (1/2, 1/2, 0, 0).
En comparant les valeurs de h en ces huit points, on trouve que le minimum sur H vaut
– 4 et qu’il est atteint au programme optimal (0, 0, 0, 1). La solution ne sautait peut-être pas immédiatement aux yeux à la lecture du problème !

[encadre]

Les polyèdres convexes

Dans l’espace à n dimensions, une équation du premier degré  \( \sum^n_{i=1}\alpha_ix_i=d\)  est celle d’un hyperplan. Ce dernier détermine deux « demi-espaces fermés », définis par une inégalité large obtenue en remplaçant dans l’écriture ci-dessus le signe d’égalité par ≤ ou par ≥.

Un polyèdre convexe est alors l’intersection d’un nombre fini de demi-espaces fermés. Son intersection non vide avec un hyperplan en est une face ; si cette intersection se réduit à un seul point, celui-ci est appelé point extrême (ou sommet) du polyèdre. Une face d’une face d’un polyèdre est également un polyèdre.

Ainsi, dans le plan, un triangle est un polyèdre convexe, ses côtés et ses sommets en sont des faces de dimension 1 ou 0.

Une particularité des polyèdres convexes est de n’admettre qu’un nombre fini de points extrêmes ; ce nombre n’est pas nul quand le polyèdre est borné.

La détermination des points extrêmes d’un polyèdre peut être obtenue systématiquement. On convertit en égalités les inégalités de la définition du polyèdre (à savoir, les n conditions de non-négativité et les m vraies contraintes) définissant l’ensemble E des programmes réalisables. On construit, puis on résout, tous les systèmes « de type Cramér » (c’est-à-dire possédant autant d’équations que d’inconnues, et admettant une unique solution) formés au moyen de ces n égalités. Une solution X = (x₁, x₂… x_n) d’un tel système, si elle appartient à E (c’est-à-dire si elle satisfait à toutes les n + m inégalités), est un point extrême de E.

[/encadre]