Trouver son chemin vite et bien

Du point de vue mathématique, une carte routière peut être vue comme un graphe orienté et pondéré, c’est-à-dire un ensemble de carrefours (les sommets) reliés par des routes (les arcs) a priori à sens unique et de longueurs variables. La longueur de l’arc reliant le sommet u au sommet v est notée l (uv ).

Un graphe orienté pondéré.

Pour aller d’un sommet u à un sommet v on suit un chemin, c’est-à-dire une succession d’arcs qui nous mènent de proche en proche vers notre but. La longueur totale du chemin est simplement la somme des longueurs de chacun des arcs traversés. Par exemple, le chemin cba (l’arête cb suivie de l’arête ba) est de longueur 3 + 12 = 15. Le chemin ed, réduit à un seul arc, a pour longueur 9, la longueur de cette arête.

Il peut arriver, bien sûr, qu’un chemin passe par plus d’arc qu’un autre tout en étant de longueur inférieure. Il en va ainsi de cbda, de longueur 3 + 2 + 1 = 6, plus petite que celle de cba. Enfin, il se peut également que deux sommets ne puissent être joints par un sommet. Dans notre exemple, il est en particulier impossible d’aller de b vers e. Par convention, le « plus court chemin » de b à e est dit de longueur infinie.

L’algorithme de Dijkstra

La tâche qui nous attend va être de déterminer tous les plus courts chemins orientés à partir d'un sommet initial donné (quelconque) vers tous les autres. C'est ce que fait l'algorithme de Dijkstra, un algorithme fondamental dans le domaine de l'optimisation discrète (et dont on va donner une idée du fonctionnement).

Pour un sommet r donné, l'algorithme construit une table, LONG, faite des valeurs LONG[u] qui, à la fin, représenteront chacune la longueur d'un plus court chemin de r vers u (car il n'y a pas nécessairement unicité d'un chemin « le plus court »).

Afin de calculer et de mémoriser les plus courts chemins à partir de r, une table PARENT est utilisée. À la fin de l’algorithme, pour chaque sommet u, la case PARENT [u] contiendra non pas tout un chemin comme on pourrait s’y attendre, mais seulement un sommet (ou éventuellement rien du tout, dans certains cas).

Comment coder avec un seul sommet tout un chemin (qui peut être composé de très nombreux arcs), demandera-t-on ? C’est tout simple : PARENT [u] sera simplement le sommet qui précède u dans un plus court chemin menant de r à u. Notant v ce sommet, PARENT [v] donnera donc le sommet qui précède v dans le plus court chemin de r à u, et ainsi de suite. 

Pour construire ces deux tables LONG et PARENT, l’algorithme de Dijkstra procède par étapes, en accumulant les connaissances accumulées aux étapes précédentes. Pour commencer, on pose que LONG [u] est infini pour tout sommet u différent de r. De même, pour PARENT, en l’absence de connaissance, il nous faut mettre une valeur, souvent notée NIL (ou parfois NULL), désignant le fait que, pour l’heure, la case de la table est « vide ».

Voilà un début pas très prometteur : on ne sait rien et on note dans les deux tables que l’on ne sait rien. Les étapes suivantes vont, heureusement, venir améliorer les choses.

Pour commencer, et malgré le fait que l’on n’a pas encore parcouru le graphe, une chose est connue et certaine. Le plus court chemin de r à lui même est de longueur nulle (il n’y en a pas de plus court) ! On peut donc redéfinir LONG [r] en lui attribuant la valeur 0. PARENT [r], lui, reste à NIL car r n’a pas de prédécesseur, tous nos chemins partant de lui.

À chaque nouvelle étape, l’algorithme sélectionne et traite, parmi les sommets u pas encore traités, celui pour lequel la valeur LONG [u] est la plus petite (on le choisit arbitrairement en cas d’égalité). Lorsque l’algorithme termine le traitement d’un sommet u, ce dernier obtient le statut « traité ».

Relâchement d’arc

Le traitement du sommet u consiste à étudier dans quelle mesure notre connaissance des chemins partant de u peut s’améliorer en considérant les arêtes uv. On parle de relâchement de uv. Derrière ce vocabulaire qui n’est pas très expressif se trouve le « cœur du cœur » de la méthode (et d’autres algorithmes apparentés). Au moment du relâchement de uv, LONG [u], LONG [v], et PARENT [v] ont certaines valeurs (qui peuvent éventuellement être l’infini ou NIL). La question centrale qui est posée par le relâchement est : pour aller de r à v, est-il plus court d’y aller via le sommet u, ou bien par un chemin de longueur LONG[v] trouvé aux étapes précédentes ?

S’il est strictement plus court d’y aller via u, alors l’algorithme vient de découvrir un nouveau chemin de r à v (via u), plus court que celui qui était connu avant ce relâchement. Cette condition se traduit ici formellement par l’inégalité LONG [v] > LONG [u] + l (uv). Il convient donc de mettre à jour nos connaissances pour intégrer ce chemin plus court qui vient d’être découvert grâce à u. Pour cela, il suffit de remplacer
LONG [v] par LONG [u] + l (uv) et PARENT [v] par u.
Dans cette procédure, les cases des deux tables sont mises à jour au fur et à mesure des découvertes de chemins plus courts que ceux qui étaient connus jusqu’alors.

S’il n’est pas strictement plus court d’y aller via u, alors on ne fait rien : aucune donnée dans les tables n’est modifiée.

Lorsque tous les sommets sont traités, l’algorithme est terminé et son résultat est constitué des deux tables. La clé de l’algorithme est le théorème qui énonce que les chemins et leurs longueurs sont bien minimaux.

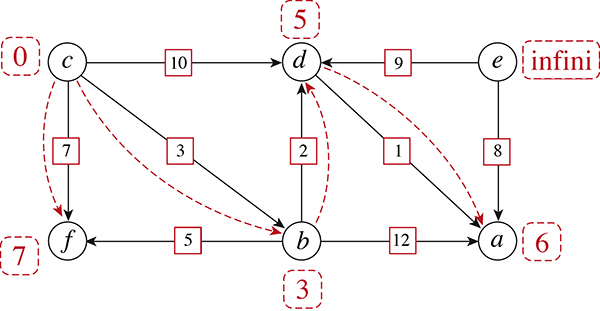
Illustrons la démarche sur notre graphe en prenant r = c. Après l’initialisation, le sommet le plus proche de c est… le sommet c lui-même (ainsi, LONG [c] = 0 et toutes les autres cases valent l’infini). Il est ainsi naturellement traité en premier. Le relâchement de chacun de ses trois arcs sortants permet d’obtenir
LONG [b] = 3, LONG [f ] = 7, LONG [d ] = 10 et PARENT [b] = PARENT [f ] = PARENT [d ] = c. Le sommet c obtient le statut « traité ».

Le sommet non traité qui a la plus petite valeur LONG (qui est en ce sens « le plus proche » de c) est b.

Relâchons ses trois arcs sortants, ba, bd et bf. Puisque LONG [a] est pour l’instant infini, le relâchement de ba donne
LONG [a] = LONG [b] + l (ba) = 3 + 12 = 15, et PARENT [a] devient b (à la place de NIL).
Ce cas est rigoureusement similaire aux cas précédents des arcs sortants de c.

Relâchons maintenant bf. Comme : LONG [f ] = 7 > LONG [b] + l (bf) = 3 + 5 = 8, la route de c vers fvia b n’est pas plus courte que celle qui était déjà en mémoire avant le relâchement. Pour cette fois, donc, on ne change rien.

Relâchons maintenant bd. Avant cela, on a LONG [d ] = 10 et LONG [b] + l (bd) = 3 + 2 = 5. Grâce à d, un chemin plus court de c vers d est trouvé. Les cases impactées sont
LONG  [ d ], qui prend la valeur 5 (à la place de 10), et PARENT [d ], qui devient b (à la place de c ). Le sommet b est désormais « traité ».

En poursuivant ainsi, on obtient la figure suivante, où une flèche en pointillés rouges de u vers v signifie que PARENT [v] = u. La valeur rouge à côté d’un sommet u désigne LONG[u]. Notez que LONG[e] n'a pas été modifié et que PARENT[e] = NIL car G ne contient aucun chemin orienté de c vers e.

Vous n'aurez plus jamais d'excuse pour ne pas emprunter le chemin le plus parcimonieux !