L'art de ne pas se croiser

Le peintre et sculpteur britannique Anthony Hill (né en 1930) fut l’un des fers de lance du constructionist group, renaissance londonienne d’après-guerre du constructivisme. Dans les années 1950, il s’intéressa de près à toute sorte d’objets mathématiques, notamment la représentation des graphes complets (voir en encadré). Rien d’insurmontable jusque-là : il s’agit de se donner un certain nombre de points, et de tous les relier les uns aux autres par des arêtes.

L’une des questions qui se posaient à l’artiste, ainsi qu’à son collègue John Ernest (1922–1994), un Américain installé à Londres depuis 1951 et à qui l’on doit notamment le ruban de Möbius de bois et de métal de la collection nationale d’art moderne international Tate, était la suivante : combien de croisements compterait le dessin final, au minimum, si l’on s’autorisait à déformer les arêtes autant que l’on veut ?

[encadre]

Les graphes complets

En combinatoire, un graphe est un ensemble de points (les sommets) dont certains sont reliés entre eux par des lignes (les arêtes). La forme géométrique des lignes n’a pas d’importance, seuls comptent les sommets qu’elles permettent de joindre (voir les Graphes, Bibliothèque Tangente 54, 2015).

Un graphe est dit complet lorsque chacun de ses sommets est relié à tous les autres. Le graphe complet à n sommets est noté K_n.

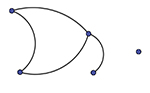
Un exemple de graphe, avec cinq sommets et quatre arêtes.

Les cinq premiers graphes complets.

Premières esquisses

Le graphe complet à deux sommets, noté K₂, ne présente aucune difficulté : il suffit de tracer un segment entre deux points. Le cas de K₃ n’est pas plus difficile : on dessine simplement un triangle ; chacun choisira celui qui lui paraît le plus esthétique… Pour quatre sommets, la question des croisements commence à émerger. La représentation la plus habituelle est la suivante, qui fait apparaître un croisement.

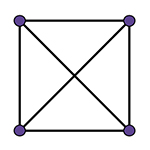
En disposant les points autrement, ou en traçant des arêtes « moins rigides », on peut toutefois éviter les croisements. Le nombre minimum de croisements de K₄ est donc, de fait, nul. On écrit : cr (K₄) = 0.

Passons au cas du graphe complet à cinq sommets. Après quelques tentatives, il semble inévitable de croiser au moins une fois les arêtes… Mais en est-on certain ?

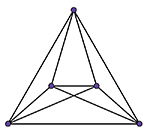
Il est possible de démontrer que cr (K₅) = 1, c’est-à-dire que toute représentation de K₅ dans le plan nécessite au moins un croisement. En fait, en utilisant astucieusement quelques résultats fondamentaux de théorie des graphes, on peut même aller plus loin. Plaçons-nous dans le cas général du graphe complet K_n. Chacun de ses sommets est relié aux n – 1 autres, et chaque arête relie deux sommets. Ce graphe compte donc \( \frac{n(n-1)}{2}\) arêtes. 

Dessinons K_n avec son nombre minimum de croisements possible, et considérons chaque croisement comme un nouveau sommet. On obtient donc un nouveau graphe, noté K_n’, qui possède n + cr (K_n) sommets. Chaque croisement de notre graphe K_n originel ayant ajouté deux nouvelles arêtes exactement, le graphe K_n’ comporte, lui, précisément \( \frac{n(n-1)}{2}+2cr(K_n)\)   arêtes.

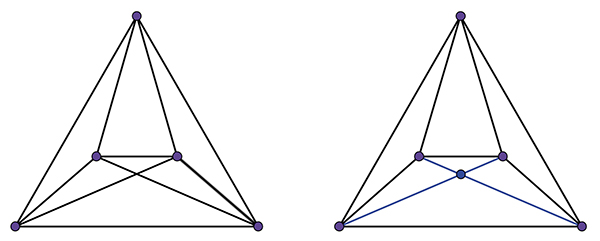
Le graphe K5 compte cinq sommets, dix arêtes (et un croisement) ;
le K5’ possède six sommets et douze arêtes (et aucun croisement).

[encadre]

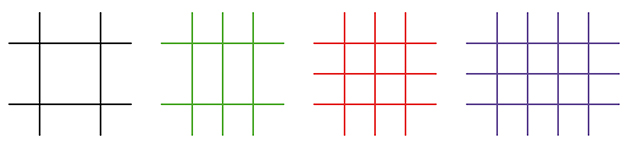
Un minimum de croisement pour un maximum de rectangles ?

Combien de rectangles peut-on représenter avec un nombre fixé N de droites ? Avec N = 3, on ne peut dessiner aucun rectangle. Avec N = 4, on ne peut guère espérer mieux qu’un unique rectangle. Avec N = 5, on peut obtenir trois rectangles. Avec six droites, on en obtient 9, et avec sept droites, on en obtient 18. Regardez bien les nombres que l’on a ainsi obtenus : 0, 1, 3, 9, 18. C’est exactement le début de la suite des nombres minimums de croisements pour les graphes complets à 4, 5, 6, 7 et 8 sommets ! Serait-ce une piste pour démontrer la conjecture exprimant cr (K_n) en fonction de n ?

[/encadre]

Dans les traces de Descartes et Euler

Que peut-on faire de cette construction ? L’idée est d’utiliser une formule énoncée par Descartes puis démontrée par Euler en 1752 : les nombres S de sommets, A d’arêtes et F de faces d’un polyèdre convexe vérifient la relation F = 2 – S + A (voir le dossier « La sage des théorèmes : la formule d’Euler » dans Tangente 174, 2017). Cette formule est valable aussi pour les graphes planaires, c’est-à-dire ceux qui peuvent se dessiner dans le plan sans croisement. Dans ce cadre, les faces sont les régions délimitées par les arêtes (en comptant la région extérieure).

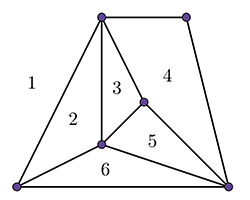
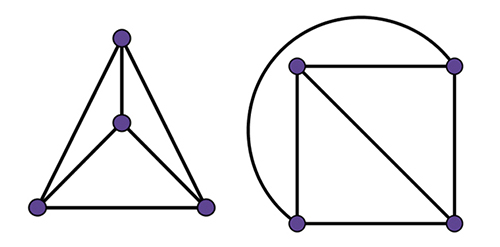
Dans l’exemple suivant, on a S = 6, A = 10 et F = 6.
On vérifie que F = 2 – S + A.

On peut facilement comprendre la formule d’Euler en dessinant un graphe étape par étape. Pour reproduire un graphe donné, on commence par dessiner un sommet. À cette étape, il y a un sommet, une arête et une face, donc on a bien S – A + F = 2.

À chaque étape, on peut dessiner :

• un sommet supplémentaire, relié par une arête à un autre sommet déjà représenté (S augmente de 1, de même que A) ;

• une arête entre deux sommets déjà figurés, auquel cas on crée une face supplémentaire (A augmente de 1, et F aussi). 

Dans les deux cas, la formule d’Euler reste vraie. En progressant ainsi de proche en proche, on parvient à construire n’importe quel graphe planaire, tout en préservant la validité de la formule d’Euler.

Chaque face est délimitée par au moins trois arêtes, et chaque arête est commune à deux faces. En un sens, donc, chaque face nécessite « au moins 3/2 arêtes ». Autrement dit, on a A ≥ (3/2) F, c’est-à-dire F ≤ 2A / 3. D’après la formule d’Euler–Descartes, on a donc
2 – S + A ≤ 2A / 3, c’est-à-dire 2 – S + A/3 ≤ 0.

Une face est bordée par « au moins trois demi-arêtes ».

Voyons à présent ce que donne notre inégalité une fois appliquée au graphe K_n’. D’après les expressions obtenues pour le nombre de sommets et d’arêtes, on a :

\( 2-(n+cr(K_n))+\frac{1}{3}\Big(\frac{n(n-1)}{2}+2cr(K_n)\Big)\leq 0.\)

Après simplification, on obtient cr (K_n) ≥ (n² – 7n + 12) / 2. Appliquée à n = 5, cette inégalité donne cr (K₅) ≥ 1. Puisque l’on a par ailleurs donné plus haut une représentation de K₅ avec un seul croisement, on a bien démontré que cr (K₅) = 1.

Pour n = 6, l’inégalité fournit cr (K₆) ≥ 3. Il y a en fait égalité, comme le montre la représentation suivante de K₆.

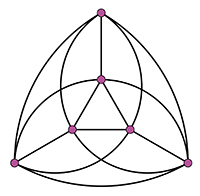
cr (K6) = 3.

Pour K₇, l’inégalité indique que six croisements au moins sont nécessaires. Dans ce cas, toutefois, l’inégalité n’est pas optimale, car on peut démontrer par ailleurs que l’on ne peut pas faire mieux que neuf croisements.

Une conjecture artistique

Anthony Hill et John Ernest sont allés plus loin, en proposant un mode de construction de K_n pour lequel le nombre de croisements semble optimal. Voici comment. Dessinons deux cercles concentriques (en pointillés sur la figure), et plaçons la moitié des sommets sur chacun des deux cercles (s’il y en a un nombre impair, on en met un de plus à l’intérieur). Relions entre eux tous les sommets du petit cercle (c ), en restant à l’intérieur de (c ). Relions également tous les sommets du grand cercle (C) entre eux, en passant cette fois par l’extérieur de (C). On relie enfin les sommets extérieurs aux sommets intérieurs, en restant dans la couronne délimitée par (c ) et (C).

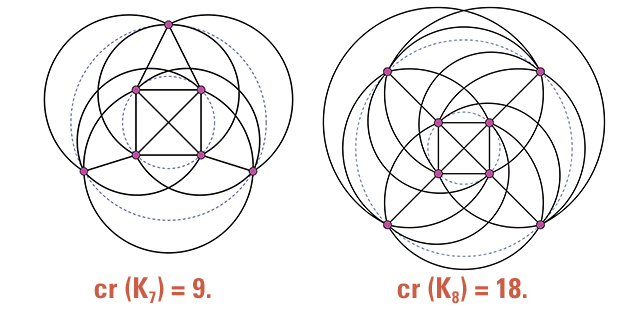
Avec un peu d’organisation, on peut montrer que, sur ces dessins, le nombre de croisements obtenus est égal à \( \frac{1}{4}\left [ \frac{n}{2}\right ] \left [\frac{n-1}{2}\right ] \left [\frac{n-2}{2}\right ] \left [\frac{n-3}{2}\right ],\) où [x] désigne la partie entière de x.
Au début des années soixante, les mathématiciens Thomas Saaty (1926–2017) et Richard Kenneth Guy (né en 1916) ont conjecturé, de façon indépendante, que ce résultat est optimal. À l’heure actuelle, le résultat est démontré jusqu’à n = 12 mais la question reste ouverte pour de plus grandes valeurs de n.
 

Avec d’autres graphes

On peut se poser le même genre de questions pour d’autres configurations que les graphes complets. C’est ce que fit le Hongrois Pál Turán (1910–1976), qui fut l’un des premiers mathématiciens à s’intéresser au problème des croisements. Alors qu’il était contraint aux travaux forcés dans une fabrique de briques durant la Seconde Guerre mondiale, il observa que chaque four était relié par des rails aux différents sites de stockage. Les chariots de briques étaient bien lourds et les pousser au niveau des intersections des rails était encore plus problématique. C’est ce souci qui fit se demander à Turán si ces croisements n’étaient pas inutilement nombreux. Était-il possible d’en obtenir un peu moins en disposant autrement les voies ferrées ?
Les connaisseurs auront reconnu ici une situation similaire au fameux problème des trois maisons (voir en encadré), qui est un cas particulier de la situation de Turán avec trois fours et trois sites de stockage.

[encadre]

Le problème des trois maisons

Trois maisons doivent être reliées à trois ressources (eau, gaz, électricité) ; est-ce possible sans croiser les canalisations ? La formule d’Euler permet de démontrer que non. En effet, chaque face d’une éventuelle solution devrait avoir au moins quatre sommets (deux maisons et deux ressources), d’où au moins quatre arêtes. On aurait ainsi 4F ≤ 2A, donc, puisque A = 9, F ≤ 4. Or on a S = 6 et A = 9, donc la formule d’Euler impose F = 5. 

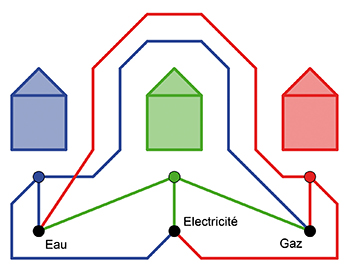
[/encadre]

En 1954, indépendamment, les mathématiciens polonais Kazimierz Urbanik (1930–2005) et Kazimierz Zarankiewicz (1902–1959) ont pensé démontrer que le nombre minimum de croisements pour relier n fours à m sites de stockage est égal à \( \left [ \frac{n}{2}\right ] \left [\frac{n-1}{2}\right ] \left [ \frac{m}{2}\right ] \left [\frac{m-1}{2}\right ].\) Leur idée tient en une figure telle que la suivante (pour deux entiers m et n, on note K_m,n le graphe tel que m des sommets sont reliés aux n autres sommets).

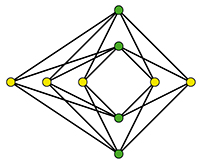
 cr (K5,4) = 8.

Onze ans après la publication du résultat, Gerhard Ringel (1919–2008) et Paul Chester Kainen (né en 1943) ont toutefois détecté une erreur subtile dans la démonstration. Cinquante ans plus tard, cette erreur n’a pas encore pu être réparée, si bien que le résultat demeure à l’état de conjecture. Avis aux amateurs !

[encadre]

Bouée de secours

Dessiner un graphe sans croisement peut s’avérer impossible sur une feuille de papier. Le problème ne vient cependant pas forcément du graphe, mais de la feuille ! Si l’on s’amuse à dessiner le graphe sur un tore (un objet de la forme d’une bouée), ce qui était insoluble devient parfois possible.

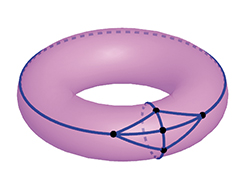
K₅ dessiné sans croisement sur le tore.

Une solution à l’énigme des trois maisons sur le tore.

[/encadre]