
Heaviside : l’arrivée des fonctions discontinues en physique
 Oliver Heaviside (1850–1925).
Oliver Heaviside (1850–1925).
Le physicien britannique autodidacte Oliver Heaviside est réputé pour avoir reformulé les équations de Maxwell. Il est par ailleurs passé à la postérité en introduisant une fonction « marche d’escalier », qui est simplement l’indicatrice de l’ensemble des réels positifs.
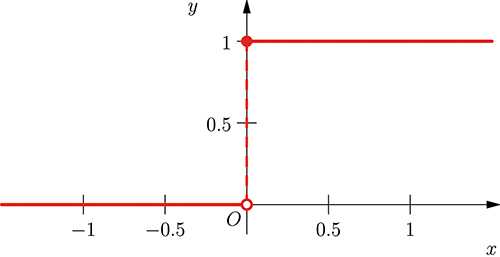
La fonction de Heaviside.
C’est pour ses recherches en électricité qu’il a introduit une fonction présentant une discontinuité, un saut. La fonction de Heaviside ou échelon vaut 0 pour les valeurs strictement négatives de l’argument, et 1 pour les valeurs positives. C’est un objet mathématique parfaitement bien défini, mais qui en son temps a pu surprendre : pourquoi des fonctions discontinues possèdent-elles une utilité en physique, ici dans l’étude des systèmes en automatique ?
Distributions : les maths pour mettre de l’ordre
On doit au mathématicien français Laurent Schwartz, membre éminent du collectif Bourbaki, dans les années 1940, l’introduction de classes de fonctions généralisées appelées distributions. L’idée des distributions est d’introduire des objets dont l’intégrale avec des fonctions « suffisamment régulière » est définie. Il s’agit d’une vision « dynamique », et non « statique ». Toute fonction au sens habituel du terme est une distribution. Avec ce nouvel éclairage, la fonction de Dirac devient une distribution. Mieux : elle devient la dérivée faible (la « dérivée » au sens des distributions) de la fonction de Heaviside !
Références :
• Dossier « Mathématiques du partage et des distributions ». Tangente SUP 77–78, 2014.
• Méthodes mathématiques pour les sciences physiques. Laurent Schwartz, Hermann, 1961.
Dirac et son δ
 Paul Dirac (1902–1984).
Paul Dirac (1902–1984).
En 1930 est publié un livre fondateur, aux enseignements précis et lumineux. Y sont exposés en particulier les principes de la mécanique quantique. L’auteur, Paul Dirac, présente une généralisation qui s’avère délicate puisqu’il s’agit de formuler, dans un contexte continu, des relations déterminées dans un cadre discret. En 1927 déjà, il élaborait une théorie des transformations qui lui permettait de montrer que les représentations matricielles de Heisenberg et l’équation de Schrödinger sont, d’une certaine manière, équivalentes. Dans sa « démonstration », Dirac introduit une « fonction » ou « impulsion » delta, notée δ, dont la « définition formelle » est :
C’est à première vue une aberration mathématique ! Une fonction nulle partout sauf en un point ne peut avoir une intégrale égale à 1…
.jpg)
Le delta de Dirac.
Cette notation commode est pourtant introduite dans le chapitre V du livre. Dirac prend soin de prévenir « qu’il n’est pas à craindre que l’introduction de la fonction δ dans nos calculs rende la théorie moins rigoureuse qu’elle ne l’était jusqu’à présent, toute équation qui renferme la fonction δ peut être écrite sous une forme équivalente quoique moins commode dans laquelle la fonction disparaît complètement ; c’est une notation pratique ».
Malgré ces précautions, les mathématiciens purs se sont rebellés. Le collectif de mathématiciens Bourbaki « entra en guerre » contre la « fonction » δ.
Lire la suite gratuitement