Les symétries dans la physique du XX^e siècle

Les symétries peuvent être codées dans une structure algébrique de groupe. L’une des propriétés principales des groupes est la loi de composition interne : l’application successive de deux opérations est encore une opération du groupe. Cette méthodologie a contribué à la découverte de nouvelles particules élémentaires.

En relativité, il existe les transformations de Poincaré–Lorentz ; elles forment un groupe. En physique nucléaire, l’interaction forte, qui assure la cohésion du noyau, est indépendante de la charge, qui est liée à une propriété d’invariance interne par symétrie d’isospin entre le neutron et le proton et correspond au groupe de symétrie SU(2).

Les symétries de jauge

Beaucoup de transformations s’effectuent dans l’espace usuel. Elles sont de fait assez faciles à visualiser. Il est possible d’envisager des transformations qui, sans affecter l’espace et le temps, changent les variables dynamiques d’un système. On appelle les symétries qui en résultent symétries internes.

Une transformation de jauge est définie comme une opération sur un point de l’espace-temps  \( (\vec{x}, t)\)  qui agit en fonction de paramètres qui sont des fonctions arbitraires de \( (\vec{x}, t).\)

L’invariance de l’équation de Schrödinger

L’exemple le plus simple de transformation de jauge est l’invariance de l’équation de Schrödinger. En effet, au centre de cette équation, on trouve la fonction d’onde de  \( \Psi(\vec{x},t).\)  C’est une application à valeurs complexes du point \( \vec{x}\)   de l’espace et du temps t, et seul son module (qui est égal à 1) possède une signification physique : sa phase n’est pas une quantité mesurable.

Il est possible d’écrire mathématiquement un changement de phase de la fonction d’onde comme suit : à   \( \Psi(\vec{x}, t)\)  , on associe   \( e^{i \theta} \Psi(\vec{x}, t)\)  , où θ est une phase constante. Avec une telle transformation, l’équation de Schrödinger reste invariante, ce qui constitue une symétrie (certes abstraite). Cette invariance de jauge est en outre une symétrie interne car elle n’affecte pas le système de coordonnées. C’est le physicien russe Vladimir Aleksandrovitch Fock (1898–1974) qui a mis en évidence cette symétrie de jauge interne à la physique quantique.

Fock s’est ensuite demandé quelles seraient les forces nécessaires pour rendre cette invariance locale (au sens où θ dépendrait de \( (\vec{x}, t)\)  ). Les forces électromagnétiques sont une réponse : si la phase de la fonction d’onde n’est pas une constante mais une fonction arbitraire de  \( \Psi(\vec{x}, t)\)  , cela décrit le mouvement d’une particule chargée dans un champ électromagnétique. 

Le modèle standard de la physique des particules est basé sur les théories de jauge qui sont liées aux propriétés de symétrie des phénomènes. Avec l’électromagnétisme dans sa version quantique, l’électrodynamique quantique, c’est le champ de l’électron qui présente des symétries. Il n’est par contre pas invariant par rapport à une transformation de jauge locale car la symétrie du champ est globale.

Le groupe des symétries d’une figure

Plaçons-nous dans le plan et considérons une figure F, un carré ABCD par exemple. Pour s’adapter au langage des physiciens, appelons symétrie de la figure F toute isométrie la conservant. Dans ce cadre, l’identité conserve toute figure F. On démontre aussi que la composée de deux isométries conservant F conserve également F, de même que l’inverse de toute isométrie conservant F. On a affaire à une structure de groupe. Dans le cas du carré, le groupe des symétries est constitué de huit éléments.

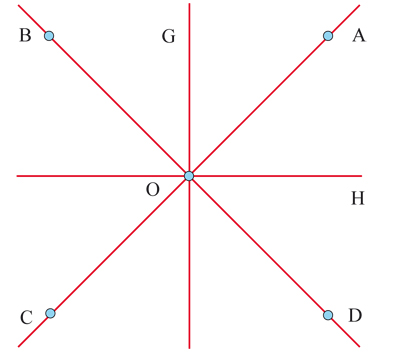
Les huit éléments du groupe de symétries du carré se scindent en quatre rotations (l’identité et les rotations de centre O, le centre du carré, et d’angles 45°, 90° et 135°), qui forment un sous-groupe, et de quatre symétries d’axes (OA), (OB), (OH) et (OG). Dans le cas général, le groupe d’une figure se réduit à l’identité si elle ne possède aucune symétrie. La question se généralise en dimension supérieure et également dans les espaces complexes.

Groupe orthogonal et groupe unitaire

Une isométrie du plan usuel est une application linéaire conservant les longueurs. L’exemple le plus simple d’isométrie est l’identité. Les exemples plus élaborés sont les rotations et les symétries axiales. En fait, on a ainsi décrit entièrement l’ensemble des isométries ! Cet ensemble est noté O(2) et appelé groupe orthogonal d’ordre 2. L’ensemble des rotations, SO(2), est appelé groupe spécial orthogonal d’ordre 2. On peut également classer les isométries selon leur déterminant : les rotations sont de déterminant égal à 1, les autres de déterminant égal à –1. 

La question se généralise dans trois directions, selon la dimension tout d’abord. Pour l’espace vectoriel réel, on obtient O(3) et SO(3) et, de façon plus générale, O(n ) et SO(n ). On peut généraliser aussi la question aux espaces affines réels, puis aux espaces complexes. Le produit scalaire change alors de sens. Dans le cas du plan réel, il s’écrit \( (\vec{\text{V}}, \vec{\text{V'}}) = xx'+yy'\)   où (x, y ) sont les coordonnées de  \( \vec{\text{V}}\)  dans une base orthonormée et de même pour \( \vec{\text{V'}}\) . Dans le cas du plan complexe, on remplace les coordonnées de  \( \vec{\text{V}}\) par leurs conjugués. On obtient ainsi le groupe unitaire d’ordre 2, U(2), et le groupe spécial unitaire d’ordre 2, SU(2). De même pour U(3) et SU(3) et, plus généralement, pour U(n) et SU(n), qui sont des groupes de Lie (groupes dotés d’une structure pour laquelle la composition et l’inversion des symétries sont deux opérations différentiables).

Insaisissable « théorie du tout »

Il n’existe que quatre interactions dans l’univers : la gravité, l’électromagnétisme, l’interaction nucléaire forte et l’interaction nucléaire faible. Les trois dernières ont été rassemblées dans le même langage des groupes de Lie. Le Graal de la physique est de trouver un cadre théorique unique permettant de décrire les quatre interactions.

L’idée est de modéliser les particules au moyen d’un modèle géométrique. L’électromagnétisme est décrit par U(1). L’interaction faible est décrite par SU(2). Leur unification s’est faite dans un groupe de Lie combinant U(1) et SU(2). L’interaction forte est décrite par SU(3). Le modèle standard, le plus efficace aujourd’hui (et conforté par la découverte du boson de Higgs), est décrit par un groupe de Lie combinant U(1), SU(2) et SU(3). Dès 1973, Howard Mason Georgi III et Sheldon Lee Glashow remarquent que U(1), SU(2) et SU(3) sont des sous-groupes de SU(5). Ils proposent donc d’utiliser ce groupe de Lie. Le nouveau modèle semble pertinent mais prédit des phénomènes qui ne sont pas observés.

Les groupes de Lie sont tous connus depuis la fin du XIX ^e siècle. Parmi eux figurent cinq groupes exceptionnels : G₂, F₄, E₆, E₇ et E₈. Ils jouent un grand rôle en mathématiques. En 2007, Antony Garrett Lisi propose d’utiliser le « plus grand » des groupes de Lie exceptionnels, E₈, découvert en 1887 par Wilhelm Karl Joseph Killing. Lisi parvient à intégrer la gravitation ! Ce qui a fait grand bruit en 2007. Hélas, ce modèle ne rend pas compte de tous les phénomènes observés et il est contredit par plusieurs expériences. Alors, une théorie physique du tout existe-t-elle ?

Références :

Une théorie géométrique du tout. Garrett Lisi et James Weatherall, Pour la science 400, février 2011. 

Le site MyToE de J Gregory Moxness, https://theoryofeverything.org/theToE/