La relativité générale est une théorie introduite par Einstein en 1915 pour décrire la gravitation. Jusque-là, l’attraction exercée par un corps A sur un corps B était décrite par une force, exprimée par la loi de la gravitation universelle de Newton, et le mouvement de chacun des corps était obtenu grâce aux lois du mouvement de ce même Newton. Ces lois permettaient d’obtenir une description assez fidèle des expériences réalisées à l’époque, mais il y avait déjà une observation astronomique que les mathématiciens et physiciens n’arrivaient pas à décrire avec la théorie disponible : l’orbite de la planète Mercure n’est pas une ellipse parfaite, comme le prédiraient les lois de Newton si le soleil et Mercure étaient les deux seuls astres de l’univers. Surtout, la prise en compte de l’influence des autres planètes du système solaire sur le mouvement de Mercure ne permet pas de décrire totalement ce « défaut ».

L’émergence de l’espace-temps

La physique a beaucoup évolué entre le XVII^e siècle et le début du XX^e : la théorie de l’électromagnétisme et la relativité restreinte notamment sont venues bousculer le paysage. Le principe d’« action à distance » présent dans la gravitation universelle de Newton n’était pas compatible avec ces nouvelles théories, qui requièrent l’introduction d’un espace-temps qui n’est pas celui du brillant scientifique britannique.

p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; line-height: 12.5px; font: 9.0px 'Block Berthold Condensed'; color: #acc740} span.s1 {font-kerning: none}

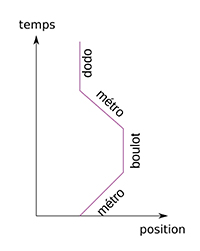
Trajectoire d’un observateur « métro–boulot–dodo ».

Un point dans l’espace-temps s’appelle un évènement : c’est un endroit à un certain instant donné. Pour le décrire, on peut utiliser des coordonnées (par exemple des coordonnées GPS et une date). Ces coordonnées n’ont rien d’absolu : on pourrait choisir de placer l’an 0 en 622, ou convenir que le méridien de référence passe par Paris. Quoi qu’il en soit, pour décrire la trajectoire d’un corps dans l’espace-temps, il est nécessaire de choisir un repère, ou référentiel.

L’espace-temps de Newton postule l’existence d’horloges universelles : on peut parler de l’ensemble des évènements ayant lieu à un instant t. Par contre, il ne postule pas l’existence d’un référentiel universel. En fait, les équations du mouvement sont inchangées entre deux référentiels en translation rectiligne uniforme l’un par rapport à l’autre. La vitesse quant à elle est une quantité qui dépend du référentiel : si je marche à 3 km/h dans un train allant à 100 km/h, dans le référentiel de la gare, j’avancerai à 103 km/h.

L’un des principes fondateurs de la relativité restreinte est qu’il est impossible d’aller plus vite que la vitesse de la lumière c, qui est une constante universelle. La loi d’addition des vitesses de Newton ne peut donc plus être valable : si un observateur avance à 3 km/h dans une fusée allant à la vitesse c, sa vitesse ne sera pas (c + 3) km/h ! Pour lever ce paradoxe, il a fallu changer de point de vue sur l’espace-temps. Ainsi, le futur d’un évènement est l’ensemble des points de l’espace-temps qu’il est possible d’atteindre sans dépasser c. Dans l’espace-temps de la relativité restreinte, cela n’a plus de sens intrinsèque de dire que deux évènements sont simultanés : le temps est une donnée qui dépend de l’observateur O (un objet ou une personne). Sa trajectoire dans l’espace-temps est appelée une courbe de genre temps.

La théorie de la relativité restreinte, introduite par Albert Einstein en 1905, dans la continuité de travaux de mathématiciens comme Henri Poincaré et Hendrik Antoon Lorentz, réconcilie la mécanique de Newton avec la théorie de l’électromagnétisme de Maxwell, postulée au cours du XIX^e siècle. Dans la théorie de l’électromagnétisme, la force électrique « à distance » entre deux particules chargées est en faite transmise par une onde (ou un photon avec la dualité onde–particule), allant à la vitesse de la lumière. Au début du XX^e siècle, la gravitation est, elle, toujours décrite par les lois de Newton de la gravitation universelle, et l’action gravitationnelle « à distance » a besoin d’une explication !

Des droites et des triangles « courbés »

 Pour arriver à la théorie de la relativité générale, qui rend compatible la gravitation et la relativité restreinte, Einstein est parti de l’observation suivante, aussi appelée principe d’équivalence. On s’intéresse à un corps A, soumis à l’attraction gravitationnelle exercée par un corps B. Les lois de Newton affirment que l’accélération de A multipliée par sa masse est égale à la force qui lui est appliquée. La masse qui apparaît dans cette relation est appelée masse inertielle ; c’est celle qui rend « plus ou moins difficile la mise en mouvement ». Or, la force qui est appliquée au corps A est la force gravitationnelle, qui est proportionnelle à la masse de A ; cette dernière, qui apparaît dans l’expression de la force gravitationnelle, est appelée masse grave (à l’époque de Descartes, on parlait de chute des graves plutôt que de chute des corps, du latin gravis, « pesant »). Si la masse inertielle est égale à la masse grave, alors il est possible de simplifier par celle-ci dans les équations du mouvement, ce qui signifie que la trajectoire d’un corps dans le champ gravitationnel ne dépend pas de sa masse. Cette équivalence est un postulat qui a été confirmé par des expériences de plus en plus précises (dans la dernière en date, en 2017, la précision obtenue pour le rapport entre masse grave et masse inertielle est de  \( 2\times 10^{-14}).\)

Les trajectoires des corps qui ne sont soumis à aucune force sont des droites de l’espace-temps. Il est cependant impossible de s’isoler du champ gravitationnel et, comme le principe d’équivalence l’illustre, n’importe quel corps, quelque soit sa masse, y est soumis : il faut donc changer « soumis à aucune force » par « soumis seulement à l’action de la gravitation », ou « en chute libre ». Évidemment, la trajectoire d’un corps soumis seulement à l’action de la gravitation, comme la trajectoire de la Terre autour du soleil, ne ressemble pas tellement à une « droite linéaire » comme on se l’imagine. L’idée de la relativité générale d’Einstein est de voir ces trajectoires comme des « droites » dans un espace-temps « courbé ».

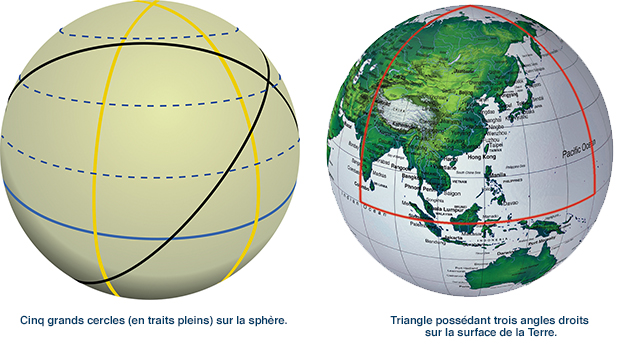
On peut déjà essayer de se demander comment on peut définir, pour commencer, une « droite » sur une sphère. Plus l’on « zoome » sur un point précis de la sphère, plus on a l’impression que cette surface est plate. En traçant une droite sur une feuille de papier, et en posant la feuille au sol, on obtient presque un morceau de droite sur la Terre, que l’on peut compléter en mettant des feuilles de papier bout à bout, de la manière « la plus plate possible ». Les courbes tracées ainsi sur la sphère sont des géodésiques : ce sont les courbes qui minimisent les distances entre deux points donnés d’une surface tout en restant incluses dans cette surface. Par exemple, l’équateur et les méridiens sont des géodésiques*, mais pas les parallèles (si deux villes sur Terre se trouvent sur un même parallèle, il existe un grand cercle qui les contient et alors la plus courte distance entre ces deux villes sera un arc de ce grand cercle, et non le chemin qui emprunte le parallèle).

La géométrie sur la sphère est ainsi assez différente de celle qui se pratique traditionnellement sur une feuille de papier. La somme des angles dans un triangle n’est pas égale à 180 degrés : il faut lui ajouter une contribution proportionnelle à la surface du triangle multipliée par une constante, qui est proportionnelle à la courbure R de la sphère. Plus précisément, la somme des angles (en radians) est égale à π plus l’aire du triangle divisée par R². De sorte que lorsque l’on dessine un triangle sur la feuille posée à même le sol son aire multipliée par la courbure de la Terre donne une contribution négligeable à la somme des angles. Mais à plus grande échelle, on peut dessiner un triangle possédant trois angles droits !

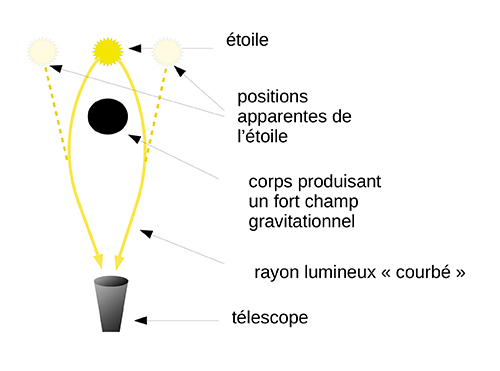
Dans une géométrie courbée, enfin, deux droites peuvent se couper en plusieurs points. Sur notre sphère, deux méridiens se rencontrent au pôle Nord et au pôle Sud. Cela permet en fait de comprendre quelques observations spectaculaires, comme les mirages gravitationnels (voir les schémas ci-dessous).

Redoutables équations d’Einstein !

La présence d’un trou noir (ou de n’importe quel corps massif) courbe l’espace-temps. Ainsi, il se peut que des rayons partant de l’étoile, qui suivent des géodésiques, se coupent en deux points : au niveau de l’étoile, et sur la lentille du télescope ; on observe alors plusieurs images distinctes de la même étoile.

Un anneau d’Einstein est un cas particulier de mirage gravitationnel. Il correspond à la déformation d’une source lumineuse qui passe à travers une lentille gravitationnelle formée par un corps céleste extrêmement massif.

Pour formuler plus précisément sa théorie de la relativité générale, Einstein a fait appel à un ami mathématicien, Marcel Grossmann, qui lui a enseigné les notions géométriques développées au cours du XIX^e et au début du XX^e siècle, notamment par des mathématiciens italiens comme Gregorio Ricci-Curbastro ou Tullio Levi-Civita.

La théorie de la relativité générale d’Einstein de 1915 peut être résumée de la manière suivante : la matière contenue dans l’univers courbe l’espace-temps. Une équation précise, faisant intervenir la courbure de Ricci, décrit ce phénomène. Résoudre les équations d’Einstein permet de connaître la métrique de l’espace-temps, donc de calculer les géodésiques, et ainsi de déterminer les trajectoires des corps soumis seulement à l’action de la gravitation.

Des équations aux prédictions étonnantes

Les équations d’Einstein sont en général très difficiles à résoudre, car l’objet courbure est compliqué ! Le premier angle d’attaque pour les étudier est de faire des hypothèses simplificatrices, comme par exemple supposer que l’espace-temps est à symétrie sphérique. C’est ce que Karl Schwarzschild a fait en 1916, et qui lui a permis de découvrir une solution particulière, dont l’impact a été phénoménal. La solution de Schwarzschild avait pour but initial de décrire la géométrie d’un espace-temps à symétrie sphérique, courbé par la présence d’une étoile de masse m. C’est un modèle efficace pour calculer les corrections relativistes dans le système solaire, qui permet notamment d’expliquer la précession de l’orbite de Mercure autour du soleil. Hélas, Schwarzschild est mort dans les tranchées en mai 1916 ; il n’a donc pas été témoin des prédictions étonnantes apportées par sa solution. En effet, en étudiant cette dernière de manière théorique, les physiciens ont pu faire l’hypothèse de l’existence de trous noirs, qui sont des zones de l’espace-temps où la gravitation est si forte que même les rayons lumineux y sont piégés.

Une autre prédiction donnée par l’étude des équations d’Einstein est l’existence d’ondes gravitationnelles. Toute perturbation non stationnaire dans l’univers va générer ces déformations de l’espace-temps se propageant, à la manière d’une onde, à la vitesse de la lumière.

Les équations d’Einstein de la relativité générale ont plusieurs points communs avec les équations de l’électromagnétisme. Le mouvement d’un électron va générer des ondes électromagnétiques, qui vont modifier le champ électrique environnant, et donc les forces auxquelles seront soumises les charges présentes. De la même manière, un mouvement de masses dans l’univers va générer des ondes gravitationnelles, qui vont déformer l’espace-temps sur leur passage. Imaginons par exemple une étoile qui « grossit » pour passer d’une masse m à une masse M. Le champs gravitationnel n’est pas le même dans les deux cas : la transition d’un modèle à l’autre se fait sous l’action d’ondes gravitationnelles.

Leur très faible amplitude les rend difficiles à observer ! En 2017 cependant, les interféromètres Ligo et Virgo ont détecté des ondes gravitationnelles émises lors de la coalescence (ou « fusion ») de deux trous noirs.

Les deux bras de l’interféromètre Virgo, situé à Cascina, près de Pise (Italie), sont longs de trois kilomètres. En mesurant une infime variation de la longueur de ces bras à l’aide d’un faisceau laser, on détecte le passage d’ondes gravitationnelles.

Les équations d’Einstein sont loin de nous avoir dévoilé tous leurs mystères. Pour les dompter, il faut aller au-delà des solutions particulières (comme par exemple la solution de Schwarzschild) et étudier les solutions les plus générales possibles. Dans les années 1950, la mathématicienne française Yvonne Choquet-Bruhat a montré que l’on pouvait écrire les équations d’Einstein comme un problème aux données initiales. Pour comprendre ce que cela signifie, faisons le parallèle avec une balle que l’on lance, dont la trajectoire est obtenue en résolvant les équations de Newton : si l’on connaît la position et la vitesse de la balle à un temps t, on peut déterminer toute sa trajectoire. De la même manière, si l’on connaît la métrique sur l’espace à un temps t, ainsi que la vitesse de déformation de l’espace à cet instant, on peut déterminer la géométrie de l’espace-temps pour des temps « proches » de t. Les équations d’Einstein font partie des équations aux dérivées partielles non linéaires, tout comme les équations de Navier–Stokes. Le caractère non linéaire implique que des perturbations tout à ait régulières peuvent conduire à la formation de singularités. Il est conjecturé que les singularités sont toujours « cachées à l’intérieur d’un trou noir » : on ne peut donc pas les observer physiquement (c’est la fameuse conjecture de la censure cosmique, voir FOCUS dans l'article « Le tenseur : un outil indispensable »). Cela n’empêche pas les mathématiciens d’essayer d’expliquer ce qui s’y passe !

 * Sur une surface sphérique, une géodésique, appelée aussi grand cercle, est définie par l’intersection de la sphère avec un plan passant par son centre.