Dès sa forme restreinte de 1905, la théorie de la relativité bouscule de façon définitive les idées anciennes sur le temps. Le terme de « relativité » colle bien sûr à Einstein, qui est celui qui lui a donné sa forme moderne. En un sens pourtant, l’idée apparaît déjà trois siècles plus tôt sous la plume de Galilée.

La relativité galiléenne se fonde sur l’observation qu’il nous est impossible de ressentir que nous sommes en mouvement si nous nous déplaçons « tout droit et à vitesse constante ». L’expérience peut être faite quotidiennement dans un train en marche : lorsqu’il n’y a pas de soubresaut, le voyageur se sent comme immobile. La traduction théorique de cette observation est qu’il n’existe pas dans l’univers un repère privilégié, au sens où aucun phénomène mécanique ne permet d’en distinguer un par rapport à ceux en mouvement rectiligne uniforme par rapport à lui.

Pas de référentiel absolu

Grâce aux équations de l’électromagnétisme de Maxwell, Einstein comprend alors que la relativité du mouvement concerne aussi les phénomènes électromagnétiques, et pas seulement les phénomènes mécaniques. Or si les premiers ne permettent pas non plus de savoir si l’on est dans le train ou sur le quai, c’est donc que la vitesse d’un rayon lumineux doit sembler la même dans les deux situations, y compris si, disons, le train va dans le même sens que le rayon – alors qu’il nous semblerait logique que, dans cette situation, le voyageur voie la lumière avancer moins vite.

L’explication générale est que le temps ne s’écoule pas de la même manière sur le quai et dans le train : chacun dispose de « son temps propre », à partir duquel il mesure des vitesses, et il n’y en a pas un qui soit « meilleur » ou « plus valable » que l’autre.

Ce principe de relativité (restreinte) étant posé, reste à forger une structure mathématique à même de rendre compte de ce genre de bizarreries. Pour cela, la géométrie classique, celle d’Euclide, reprise par Newton, doit laisser la place à quelque chose de neuf. Ce sera l’espace de Minkowski.

Pour intégrer le temps, un premier pas consiste à ajouter une coordonnée temporelle à l’espace. De sorte à ne pas se retrouver avec quatre dimensions (ce qui ne pose pas de problème théorique majeur mais rend la visualisation difficile), on simplifie volontiers en ne considérant qu’une seule dimension d’espace. L’univers est alors réduit à une simple droite (en une seule dimension). Sur le schéma, la coordonnée x (horizontale) permet de localiser les points sur cette droite, tandis que le temps t est en coordonnée verticale.

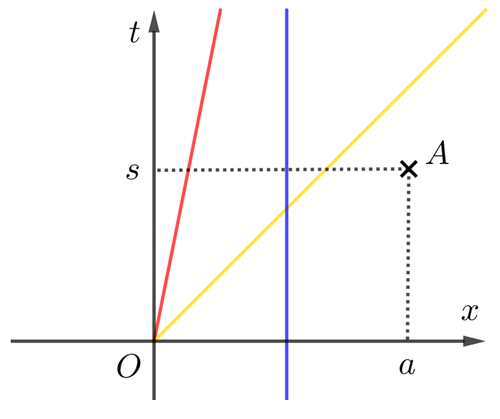
Ces axes de coordonnées n’ont rien d’absolu, ils ne correspondent qu’au point de vue d’un observateur situé en O et à un instant qu’il décide de définir comme temps zéro – qui, tout comme pour son choix de l’origine O sur la droite, n’engage que lui.

La droite verticale bleue correspond à une particule immobile par rapport à l’observateur. Sa permanence dans le temps se traduit par le trait continu qui la représente, son immobilité se lit dans sa disposition verticale (c’est-à-dire à abscisse constante).

La demi-droite rouge correspond à une particule lancée par l’observateur dans le sens des x croissants, et qui se déplace à vitesse constante. Enfin, la demi-droite jaune (première bissectrice) correspond à un rayon lumineux émis dans le sens des abscisses croissants par l’observateur à son temps zéro. Cela implique que la vitesse de la lumière est ainsi posée comme égale à l’unité.

Changement de signe

Reste à définir une structure géométrique qui fasse apparaître sur cet espace les phénomènes de la théorie de la relativité restreinte. L’élément fondamental tient à une notion spécifique de distance entre les points – qu’on appelle d’ailleurs plutôt évènements. Prenons l’évènement A de coordonnées (a, s). En géométrie ordinaire, on calculerait la distance OA à partir du théorème de Pythagore, en écrivant que OA² = s ² + a ². La métrique de Minkowski consiste, quant à elle, à écrire que OA² = s ²–a ².

Oui, ici c’est un signe – qui remplace le signe +. Cette modification transforme à elle seule absolument tout. Elle pose des problèmes considérables, mais pour un bénéfice qui ne l’est pas moins : une mathématisation rigoureuse de la relativité !

Le premier problème est que, la valeur s ² – a ² pouvant fort bien être négative, il n’est pas toujours possible de prendre sa racine carrée pour exprimer OA (sauf à passer aux nombres complexes).

Une autre nouveauté est que si s = a alors OA² = 0, c’est-à-dire que OA = 0. (Les physiciens hurlent en lisant « s = a » à cause des questions d’unité : en réalité, on devrait écrire cs = a, où c est la vitesse de la lumière ; le fait est que, comme indiqué plus haut, on a pris c = 1.) La « distance » entre les deux évènements est donc nulle, alors même que ces deux points sont différents.

Selon que OA² est positif, négatif ou nul, on parle d’intervalle de genre temps, de genre espace ou de genre lumière. Le premier cas traduit qu’il est physiquement possible de joindre O à A, c’est-à-dire de parcourir la distance a en un temps s sans dépasser la vitesse de la lumière. Si s est positif comme sur la figure, l’évènement A peut alors être une conséquence de l’évènement O (mais pas une cause). On dit que A est dans le futur de O.

Lorsque OA² est strictement négatif en revanche, O et A ne peuvent être physiquement joints l’un à l’autre (il faudrait aller « plus vite que la lumière »). Ils ne peuvent avoir un lien causal : A est dans l’ailleurs de O (c’est le cas sur la figure).

Enfin, lorsque OA est nul, seul un rayon lumineux peut joindre les deux évènements. On se trouve alors dans le cas limite où le temps ne semble pas s’écouler : du point de vue du photon, sa trajectoire toute entière existe d’une façon simultanée.

Ces phénomènes sont bien loin des expériences de pensée que nous permettent nos habitudes courantes. L’on mesure ainsi tout l’intérêt d’une mathématisation quantitative, qui permet de naviguer dans ces réalités étranges sans commettre d’erreur et donc progressivement d’en acquérir l’intuition. Approfondir la géométrie de Minkowski permet ainsi d’éclairer des phénomènes comme l’impossibilité d’aller plus vite que la lumière, ou encore le fameux paradoxe des jumeaux.