Les transformations géométriques du plan ou de l’espace que l’on considère le plus couramment ont en général la propriété de conserver l’alignement des points, c’est-à-dire que les images de trois points alignés sont également trois points alignés. C’est le cas des rotations, des translations, mais aussi des projections orthogonales sur une droite ou sur un plan.

Ces transformations conservent également le rapport des longueurs, c’est-à-dire que si deux segments pris sur une même droite D sont tels que l’un est deux fois plus long que l’autre, il en est de même de leurs images sur la droite D’ image de D.

La translation de vecteur   \( \overrightarrow{u}\)   conserve l’alignement des points A, B et C, ainsi que la position relative de B dans le segment [AC].

L’apport des artistes

Les peintres de la Renaissance, pour représenter la profondeur, se sont intéressés à la projection de l’espace sur le plan de la toile. Cette projection est issue d’un point, l’œil. Mathématiquement, c’est ce que l’on nomme une projection centrale (voir FOCUS). Certes, celle-ci conserve l’alignement ; en revanche, ce n’est plus le cas de la proportionnalité.

On sait depuis le mathématicien allemand Felix Klein (1849–1925) combien la géométrie est friande de la recherche d’invariants. Or, il est vain d’en trouver un ne considérant que trois points alignés, puisque ceux-ci peuvent être envoyés sur trois autres points alignés quelconques par la composée de deux projections centrales. Un tel invariant ne saurait donc exister.

Au début du XIX^e siècle, plusieurs mathématiciens, comme Poncelet ou Möbius, ont mis en évidence un invariant concernant quatre points A, B, C et D alignés et deux à deux distincts. Certes le quotient   \( \frac{\overline{\rm CA}}{\overline{\rm CB}}\)   n’est pas conservé par une projection centrale, mais c'est en revanche le cas du quotient de deux tels quotients,  \( \frac{\overline{\rm CA}}{\overline{\rm CB}}: \frac{\overline{\rm DA}}{\overline{\rm DB}},\)   d'où son nom de birapport des points A, B, C et D.

On est assuré que c’est un invariant par toute bijection affine, puisque   \( \frac{\overline{\rm CA}}{\overline{\rm CB}}\)   et   \( \frac{\overline{\rm DA}}{\overline{\rm DB}}\)   le sont, mais plus généralement le birapport est un invariant par toute projection centrale, et donc par la composition de telles transformations, ce que l’on nomme depuis Chasles des homographies. La démonstration directe se fait par plusieurs applications du théorème de Thalès ; on peut aussi l’établir à l’aide du Théorème de Menelaüs (voir article « Les théorèmes de Ménelaüs et de Ceva »). Une démonstration basée sur les angles est proposée en FOCUS.

Quatre points, six birapports

La notion de birapport de quatre points deux à deux distincts et non alignés dépend de l’ordre dans lequel on les considère. Comme il existe vingt-quatre ordres possibles, correspondant à toutes les permutations de quatre éléments, on pourrait penser que l’on peut obtenir vingt-quatre birapports différents avec ces quatre points en fonction de l’ordre dans lequel on les regarde.

Or, il n’en est rien. Appelons r le birapport de (A, B, C, D) ; il est différent de 0 et de 1 puisque les quatre points sont choisis deux à deux distincts. En intervertissant A et B, le birapport est transformé en son inverse 1 / r ; il en est de même en intervertissant C et D. Donc, en le faisant simultanément avec A et B et avec C et D, le birapport est inchangé. En étudiant toutes les permutations, on constate que seule six valeurs sont possibles : r, 1 / r, 1 – r, 1 / (1 – r), r / (r – 1) et (r – 1) / r. Ces six expressions fournissent six nombres distincts pour r différent de 1/2, – 1 et 2.

Dans le plan, la notion de birapport s’étend aux droites concourantes. Considérons quatre d’entre elles, concourantes au point O, et une autre leur étant sécante.

Le birapport des quatre points d’intersection de ces droites avec la sécante ne dépend pas du choix de celle-ci. En effet, si l’on considère deux sécantes, une projection centrale de centre O envoie les points d’intersection avec les quatre droites de la première sur ceux de la seconde. Par définition, le birapport de ces quatre droites concourantes est cette valeur commune.

Ce birapport dépend uniquement des positions respectives des quatre droites suivant une relation établie par August Möbius, qui précise que le birapport de (A, B, C, D) est égal à   \( \frac{\sin \widehat{\rm COA}}{\sin \widehat{\rm COB}}: \frac{\sin \widehat{\rm DOA}}{\sin \widehat{\rm DOB}}\)   (voir FOCUS) ; on retrouve ainsi son indépendance de la sécante choisie, puisque les angles n’en dépendent pas !

Cette dernière propriété permet aussi de définir le birapport de quatre points cocycliques A, B, C et D deux à deux distincts. Considérons le cercle (F) les contenant et un point quelconque M de (F) distincts de ces quatre points. Les propriétés de l’arc capable nous indiquent que les angles   \( {\rm \widehat{CMA}, \widehat{CMB},\widehat{DMA},\, {\rm et}\,\, \widehat{DMB}}\)  ne dépendent pas du point M choisi ; la formule de Möbius nous permet d’affirmer que le birapport des quatre droites issues de M et passant respectivement par A, B, C et D ne dépend pas non plus du choix de M sur le cercle. Cette valeur commune est, par définition, le birapport de ces quatre points cocycliques.

La relation de Descartes

Quatre points distincts A, B, C et D alignés sont en division harmonique si leur birapport vaut –1. En d’autres termes, cela signifie que 

\( \frac{\overline{\rm CA}}{\overline{\rm CB}}=- \frac{\overline{\rm DA}}{\overline{\rm DB}}.\)

On peut inverser A et B, ou bien C et D, sans changer ce birapport ; on dit alors que C et D divisent harmoniquement le segment [AB].

On peut aussi intervertir le rôle des couples (A, B) et (C, D) tout en conservant la propriété d’harmonicité, puisqu’il est équivalent de dire que 

\( \frac{\overline{\rm CA}}{\overline{\rm DA}}=- \frac{\overline{\rm CB}}{\overline{\rm DB}}.\)

Prenons l’origine en A et notons b, c et d les abscisses respectives des points B, C et D. La relation d’harmonicité nous donne :

\( \frac{c}{d}=-\frac{b-c}{b-d},\)

soit, après simplification :

\( \frac{2}{b}=\frac{1}{c}+\frac{1}{d}.\)

En revenant aux mesures algébriques, on obtient la relation de Descartes :

\( \frac{2}{\overline{\rm AB}}=\frac{1}{\overline{\rm AC}}+ \frac{1}{\overline{\rm AD}}.\)

En d’autres termes, la mesure algébrique   \( {\overline{\rm AB}}\)   est la moyenne harmonique des mesures algébriques de   \( {\overline{\rm AC}}\)   et de  \( {\overline{\rm AD}}\) . Pour mémoire, la moyenne harmonique m de deux réels non nuls u et v est l’inverse de la moyenne arithmétique de leurs inverses, c’est-à-dire que 2 / m = 1 / u + 1 / v. Pourquoi « harmonique » ? Ce terme nous vient de Pythagore, qui avait défini la gamme musicale en utilisant cette moyenne : en effet, la longueur d’onde étant proportionnelle à l’inverse de la fréquence, la moyenne harmonique des fréquences correspond à la moyenne arithmétique des longueurs d’onde. Par analogie avec cette dénomination, Michel Chasles appelait le birapport le rapport anharmonique, lorsqu’il différait de – 1.

Ravissantes propriétés géométriques

Donnons-nous dans le plan deux points A et B distincts. Alors à tout point C de la droite qu’ils engendrent correspond un unique point D de cette droite tel que C et D divisent harmoniquement le segment [AB] : on appelle D le conjugué harmonique de C par rapport au segment [AB].

Comme on sait définir le birapport de quatre droites concourantes D₁, D₂, D₃ et D₄, on peut dire qu’elles forment un faisceau harmonique si leur birapport vaut – 1. La propriété suivante est utile : un faisceau est harmonique si, et seulement si, toute droite parallèle à l’une d’entre elles est divisée par les trois autres en deux segments égaux. Cela fournit une méthode de construction élémentaire du conjugué harmonique !

Autre propriété intéressante, deux droites concourantes forment avec leurs bissectrices, intérieure et extérieure, un faisceau harmonique. 

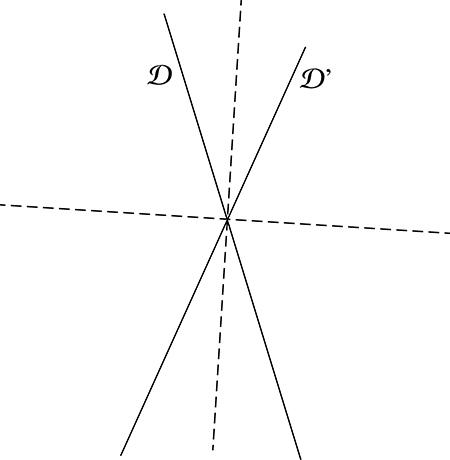
Toutes ces propriétés ravissaient les géomètres du siècle dernier, avec l’étude de notions désormais peu évoquées dans l’enseignement comme les polaires ou les quadrilatères complets. Le cadre idéal pour les traiter est celui de la géométrie projective, qui élimine un certain nombre d’exceptions et nous fait parfois voyager aux confins de l’univers sur la droite à l’infini…