Dans le livre I de ses Éléments, Euclide donne les définitions des objets de la géométrie et ajoute cinq « demandes », appelées postulats par Proclus, pour établir les fondements de sa géométrie, et des « notions communes ». Les quatre premiers postulats concernent la construction de la droite, du cercle et l’universalité de l’angle droit. Ils n’ont, au cours des temps, pas posé de problèmes. Il n’en est pas de même du plus célèbre de ses postulats, ou axiomes, le cinquième dans les éditions récentes, dit axiome des parallèles, exprimé de nos jours sous la forme : « Par un point pris hors d’une droite, il ne passe qu’une parallèle à cette droite. » Après vingt-deux siècles de recherches infructueuses, on assiste à la naissance de la géométrie hyperbolique. Le 3 novembre 1823, János Bolyai (1802–1860) écrit à son père Farkas qu’il a « créé un nouvel autre monde à partir de rien ». À la même époque, et indépendamment, Nikolaï Lobatchevski (1792–1856) obtient un résultat similaire.

La géométrie projective

Désormais, on ne parle plus de La Géométrie, mais des géométries. Sous l’impulsion de Félix Klein (1849–1925), les études géométriques consistent à rechercher les éléments invariants par un groupe caractéristique de transformations. Ainsi, pour notre usuelle géométrie euclidienne, une figure « ne change pas » (en forme et en dimension) avec les isométries que sont les rotations et les translations ; elle « ne change pas » (en forme) par un changement d’échelle, ou homothétie. L’ensemble de ces transformations constitue le groupe des similitudes et n’est rien d’autre qu’une application affine, dans le plan complexe, de la forme   \( z \mapsto az+b. \)

Issue de l’étude de la perspective, ou projection centrale, la géométrie projective ignore les notions de mesure et d’orthogonalité, et ne distingue pas les coniques entre elles.

Dans le plan (O, x, y), chacune des droites (en bleu) passant par l’origine est caractérisée avec unicité par son intersection P avec la droite (Δ) d’équation y = 1 (en rouge). Ce point P d’abscisse z = x / y (comme on le vérifie avec une application élémentaire du théorème de Thalès) définit la droite (Δ _z). Pour être tout à fait rigoureux, il faut accepter la valeur
«  \( z = \infty\)  », qui correspond à l’axe des x, ensemble des points de coordonnées ( x, 0) avec x un nombre réel.

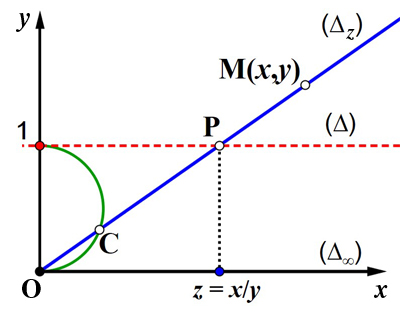
Représentation de la droite projective. 

Par le théorème de Thalès, on a OM / OP = x / z = y / 1, d’où z = x /y .

En appelant droite projective cette droite (Δ), complétée par son point à l’infini, on établit une correspondance point à point, ou bijection, entre (Δ) et les droites du plan passant par l’origine. On constate aussi qu’à tout point P de (Δ) correspond un unique point C d’un cercle (en vert) centré sur l’axe des y et tangent à l’origine. La droite projective est donc en bijection continue, ou homéomorphe, à un cercle. Les coordonnées ( x, y) d’un point sont appelées coordonnées homogènes et z = x / y est sa coordonnée non homogène, qui appartient à   \( { \overline{\mathbb{R}} = {\mathbb{R}} \cup \{+ \infty \}.}\)

Les fonctions homographiques

Une application linéaire  f du plan, de matrice   \( \quad \begin{pmatrix} a & b \\ c & d \end{pmatrix},\)   fait correspondre au point M( x, y) le point M’(ax + by, cx + dy), et transforme donc toute droite en droite. En utilisant les coordonnées non homogènes, on en déduit l’application  \( \tilde f\) de (Δ) dans elle-même telle que  

\( \tilde f (z) = \dfrac{ax + by}{cx + dy} = \dfrac{az +b}{cz +d}\)

avec z = x / y, \( \tilde f (\infty ) = a / c \)   si \( c\ne 0\)  , et \( \tilde f (\infty ) = \infty \)   sinon.

C’est l’expression générale d’une fonction homographique, ou homographie, qui est la composition d’un nombre fini de projections centrales. Ses coefficients ( a, b, c, d ) sont déterminés à un facteur multiplicatif près. On peut donc les diviser (normaliser) par l’un d’entre eux non nul, a par exemple, pour obtenir trois coefficients indépendants b /a, c /a, d /a, soit trois degrés de liberté. Cela signifie que trois points, non alignés, suffisent pour la définir.

Prenons donc, pour quatre points distincts A, B, C, D d’une droite projective, d’affixes respectives a, b, c, d, l’unique homographie φ définie par les points A, B et C telle que \( \varphi (a ) = \infty\) ,   \( \varphi (b ) = 0\)  et  \( \varphi (c ) = 1.\)  On appelle alors birapport des points A, B, C, D la valeur φ (d ), notée [A, B, C, D].

L’expression   \( \varphi (z ) = \dfrac{c-a}{c-b} \times \dfrac{z-b}{z-a} \)   définit cette homographie et φ (d ) correspond bien à la définition classique du birapport :  

\( [\text{A, B, C, D}] = \dfrac {\overline{\text{AC}}} {\overline{\text{AD}}} \times \dfrac {\overline{\text{BD}}} {\overline{\text{BC}}} .\)  

Par cette définition, et du fait que la composition d’homographies est une homographie, on constate que ces dernières conservent le birapport. Deux quadruplets de points (A, B, C, D) et (P, Q, R, S) sont donc en correspondance homographique si, et seulement si, [A, B, C, D] = [P, Q, R, S]. 

En effet, si  f est l’unique homographie telle que [P, Q, R, S] =  f (s) et s’il existe une homographie φ entre les deux quadruplets telle que φ (A, B, C, D) = (P, Q, R, S), alors, puisque  \( f\circ\varphi \)   est une homographie, on a
  \( [{\rm A,B,C,D}]=(f\circ\varphi)({\rm D})=f({\rm S})=[{\rm P,Q,R,S}].\)
La réciproque se montre de même.

Géométries non euclidiennes : au rapport !

Les géométries (dites non-euclidiennes) qui n’ont aucune parallèle (géométrie elliptique), ou au contraire plusieurs (géométrie hyperbolique), nécessitent une métrique spécifique pour définir les distances entre points et généraliser la notion de droite (une géodésique est alors une courbe de plus courte longueur, pour cette métrique, reliant deux points).

Pour étudier la géométrie dite de Bolyai–Lobatchevski, il est commode de la représenter dans notre monde euclidien par un modèle avec de nouvelles règles. Se pose alors un problème similaire à celui auquel s’est confronté le géographe Gérard Mercator (1512–1594) pour représenter une surface sphérique avec une cartographie plane…

En 1868, le mathématicien et physicien italien Eugenio Beltrami (1835–1900) établit avec la pseudo-sphère une représentation 3D de la géométrie hyperbolique qui conserve angles et distances, mais seulement sur une partie de l’espace hyperbolique. Son modèle circulaire, non conforme (qui ne conserve pas les angles), est repris par Klein en 1871.

L’espace hyperbolique y est représenté dans sa globalité par un disque sans son bord. Les points de la circonférence sont des points à l’infini inatteignables appelés idéaux. Les droites sont les cordes du cercle (comme [AB]), l’intersection de deux cordes définit un point (M par exemple) et deux points définissent une seule droite. Par un point N extérieur à la droite (AB), il passe une infinité de droites non sécantes (ici  \( [uu'],[vv'],[ww']\ldots \)   ). Il y passe également deux « parallèles » à (AB), (AP) et (BQ), qui sont déterminées par l’un des point idéaux de la droite (A ou B). Ces parallèles sont la frontière des mondes des droites sécantes et non sécantes. Notons que dans ce monde le parallélisme n’est plus une relation d’équivalence : deux parallèles à une même droite peuvent ne pas être parallèles entre elles. Par contre, elles le deviennent si elles « convergent » vers un même point idéal.

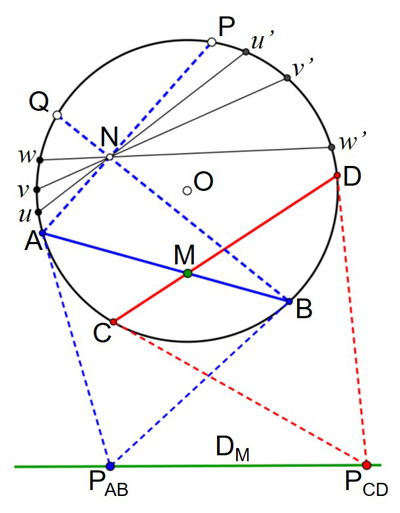
Dualité pôle–polaire dans le disque de Klein.

Cette définition de l’espace hyperbolique induit la notion de polarité, au riche potentiel (voir FOCUS). Soit par exemple à construire le symétrique du point M par rapport à la droite (D) = (UV) dans le disque de Klein. Toute droite passant par le pôle P est perpendiculaire à la droite (D). Le point symétrique M’ cherché sera donc sur la perpendiculaire (PM) qui coupe (D) en H, de sorte qu’il soit le conjugué harmonique de M par rapport à (P, H), ce qui implique [M, M’, H, P] = –1. Pour construire M’, on trace une perpendiculaire (AB) quelconque ; (BM) et (D) se coupent en Q. Le point M’ est l’intersection des droites (QA) et (PM).

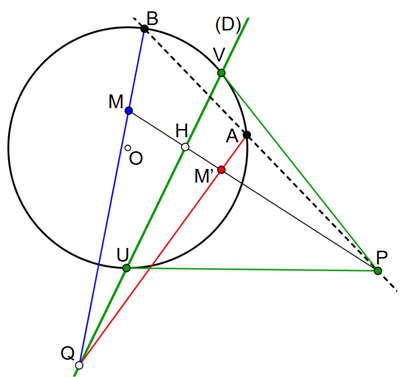
Construction d’une symétrie axiale.

En 1859, Arthur Cayley (1821–1895) ajouta à ce modèle une distance qui sera reprise par Klein. Deux points X et Y définissent une droite unique dont les points idéaux sont U et V. On remarque que, pour toute droite (DA), le cercle euclidien (C) défini par les points idéaux U et V de (DA) et par le centre O du disque de Klein contient le pôle A de (DA) et l’inverse de chacun des points de (DA). Puisque les points X et Y sont à l’intérieur du disque, le birapport r = [X, Y, U, V] des points (X, Y, U, V) est strictement positif. La distance d_DK(X, Y) des points X et Y est alors donnée par  \( d_{\text{DK}} (\text{X, Y}) = \dfrac{1}{2} | \ln r | .\)

Si X et Y sont confondus, ils partagent de manière égale le segment [UV], donc r = 1 et d_DK(X, Y) = 0.

Définition des distances dans le disque de Klein DK.

Ce choix vient du fait que pour trois points alignés A, B et C sur la droite (UV), on a la relation de Chasles multiplicative : [A, B, U, V]  [B, C, U, V]  = [A, C, U, V], expression vérifiée par simple développement. Le passage au logarithme fournit alors l’expression additive suivante : 

d_DK(A, B) + d_DK(B, C) = d_DK(A, C).

Le disque Poincaré

C’est en étudiant les fonctions automorphes telles que   \( f \left( \dfrac{az+b}{cz+d} \right) = f(z)\) qu’Henri Poincaré (1854–1912) fut amené en 1882 à modifier le modèle de Klein pour le rendre conforme. Le prix à payer fut la perte des droites, qui deviennent des arcs de cercles orthogonaux au disque DP (dit de Poincaré ). On passe de l’un à l’autre de ces modèles par une projection stéréographique, ce qui conserve les birapports.

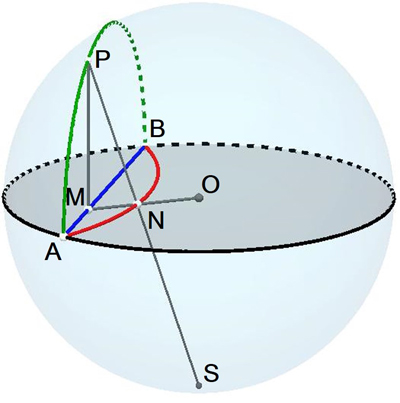
La projection stéréographique de pôle S établit une correspondance entre les droites du modèle de Poincaré (en rouge) et les droites du modèle de Klein (en bleu).

Sur la figure suivante, on justifie le nom de cette géométrie dite hyperbolique en projetant de deux façons une nappe d’hyperboloïde sur un disque unité pour obtenir les représentations de Klein (dans DK) et de Poincaré (dans DP).

Si M est un point du disque situé à la distance euclidienne r de l’origine O, la droite (OM) est un diamètre du disque et, en reprenant la distance de Klein,

  \( d_{\text{DP}} (\text{O, M}) = \dfrac{1}{2} \ln \left( \dfrac{1+r} {1-r} \right).\)

La distance tend bien vers l’infini quand M s’approche du monde idéal (r = 1).

Pour r « proche » de l’origine, on peut faire l’approximation 

\( \ln \left( \dfrac{1+r} {1-r} \right) \simeq 2r,\)

ce qui explique le facteur arbitraire de 1/2 dans la définition de la distance pour obtenir une approximation euclidienne au voisinage de l’origine.

Ces quelques exemples montrent combien le birapport, invariant fondamental de la géométrie projective, elle-même mère de toutes les géométries, est incontournable dans ce « nouvel autre monde » hyperbolique !

Projection centrale d’un hyperboloïde.
Correspondance entre les droites de Poincaré (en rouge) et de Klein (en bleu).