La géométrie du triangle est inépuisable. Parmi les innombrables richesses que l’on peut y dénicher, deux résultats à l’aspect similaire sortent du lot : les théorèmes de Ceva et de Ménélaüs. Commençons déjà par nous munir d’un triangle ABC. Plaçons un point P sur (BC), un point Q sur (CA) et un point R sur (AB). Enfin, il sera commode d’utiliser la notion de mesure algébrique des longueurs : tout segment UV pourra être affecté d’un signe. La mesure algébrique   \( {\overline {\text{UV}} \)  du segment [UV] sera égale à sa longueur si l’on va de U vers V, et à l’opposé de sa longueur si l’on va de V vers U. C’est tout ce dont on a besoin pour énoncer les théorèmes de Ménélaüs et de Ceva !

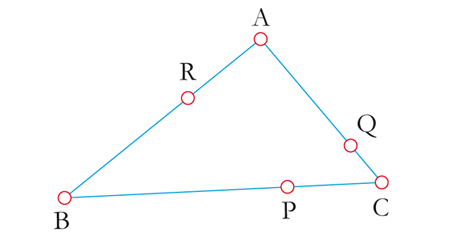
La configuration de base des théorèmes de Ménélaüs et de Ceva.

Théorème de Ménélaüs :
les points P, Q et R sont alignés si, et seulement si,

  \( {\dfrac {\overline {\text{PB}}} {\overline {\text{PC}}} \times \dfrac {\overline {\text{QC}}} {\overline {\text{QA}}} \times \dfrac {\overline {\text{RA}}} {\overline {\text{RB}}}= 1. }\)

Théorème de Ceva :
les droites (AP), (BQ) et (CR) sont concourantes ou parallèles si, et seulement si, 

  \( {\dfrac {\overline {\text{PB}}} {\overline {\text{PC}}} \times \dfrac {\overline {\text{QC}}} {\overline {\text{QA}}} \times \dfrac {\overline {\text{RA}}} {\overline {\text{RB}}}= -1.}\)

Un résultat de géométrie affine

Cela peut étonner mais la notion d’aire, ou plutôt celle de rapport d’aires, est un invariant de la géométrie affine, au même titre que les notions d’alignement, de parallélisme ou d’intersection (et contrairement à celles d’angle et de longueur, par exemple). Cette remarque a pour conséquence qu’il est possible de proposer, dans le cadre de la géométrie affine, une démonstration du théorème de Ménélaüs. Partons de l’hypothèse où les points P, Q et R sont alignés, et du cas de figure suivant.

Une configuration du théorème de Ménélaüs.

Les rapports de longueurs (sans signe) de la relation peuvent être interprétés comme des rapports d’aire. Plus précisément, les hauteurs des triangles PBR et PCR étant identiques, on a 

\( {\dfrac {\text{aire\,(PBR)} } {\text{aire\,(PCR)} } = \dfrac{\text{PB}}{\text{PC}}.}\)

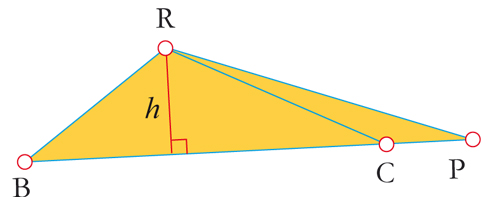
L’aire de PBR est égale à h PB/2, celle de PCR à h PC/2.

Au signe près, le premier membre de la relation de Ménélaüs s’écrit donc :

  \( {\dfrac {\text{aire\,(PBR)} } {\text{aire\,(PCR)} } \times \dfrac {\text{aire\,(QCR)} } {\text{aire\,(QAR)} } \times \dfrac {\text{aire\,(PAR)} } {\text{aire\,(PBR)} } .}\)

Cette expression se simplifie en :

  \( {\dfrac {\text{aire\,(QCR)} } {\text{aire\,(PCR)} } \times \dfrac {\text{aire\,(PAR)} } {\text{aire\,(QAR)} } . }\)

D’après le principe précédent, chacun de ces rapports d’aire est un rapport de longueurs.

On obtient  \( {\dfrac{\text {QR}} {\text{PR}} \times \dfrac{\text {PR}} {\text{QR}}, }\)  qui est égal à 1. En tenant compte du signe de chacune des mesures algébriques, on en déduit la relation de Ménélaüs.

Il reste alors à analyser l’autre cas de figure, celui où P, Q et R sont extérieurs aux côtés du triangle ABC. On évite l’analyse de ces différents cas en introduisant une notion d’aire algébrique.

La réciproque est facile à établir en considérant les points P, Q et R vérifiant la relation et R’ l’intersection de (PQ) et de (AB).

Expédition à l’infini

 Pour démontrer le théorème de Ceva, on part de P, Q et R sur (BC), (CA) et (AB) respectivement, puis on considère D, l’intersection de (PQ) et de (AB).

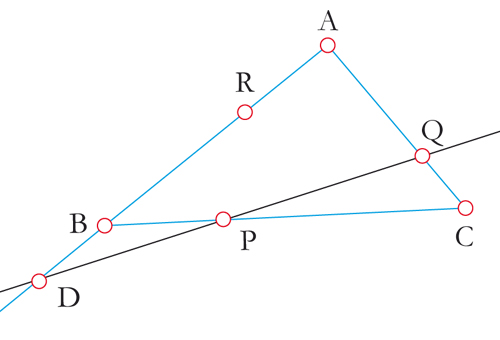
De Ménélaüs à Ceva.

D’après le théorème de Ménélaüs, on a la relation suivante :  

\( {\dfrac {\overline {\text{PB}}} {\overline {\text{PC}}} \times \dfrac {\overline {\text{QC}}} {\overline {\text{QA}}} \times \dfrac {\overline {\text{DA}}} {\overline {\text{DB}}}= 1. }\)

Or, la relation cherchée est : 

\( {\dfrac {\overline {\text{PB}}} {\overline {\text{PC}}} \times \dfrac {\overline {\text{QC}}} {\overline {\text{QA}}} \times \dfrac {\overline {\text{RA}}} {\overline {\text{RB}}}= -1. }\)

Il s’agit donc de montrer que l’on a :

\( {\dfrac { \dfrac {\overline {\text{RA}}} {\overline {\text{RB}}}} { \dfrac {\overline {\text{DA}}} {\overline {\text{DB}}}} = \dfrac {\overline {\text{RA}}} {\overline {\text{RB}}} \times \dfrac {\overline {\text{DB}}} {\overline {\text{DA}}} = [ \text{A, B, D, R}] = -1,}\)

où [A, B, D, R] est le birapport de A, B, D et R. Donc il suffit de montrer que ce birapport est égal à –1 si, et seulement si, les trois droites (AP), (BQ) et (CR) sont concourantes.

 Configuration avant l’envoi de la droite (CR) « à l’infini ».

Comme, pour des droites, « être concourantes » est une notion projective, on peut « envoyer la droite (CR) à l’infini ». Dans ce contexte, (AP) et (BQ) sont deux droites parallèles, puisqu’elles se coupent sur la droite à l’infini (CR). De même, (AQ) et (PB) se coupent (en C) sur la droite à l’infini (CR) ; elles sont donc parallèles.

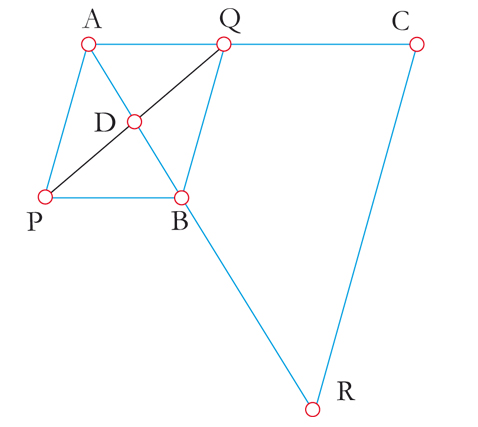
Figure après transport de la droite (CR) à l’infini.

Ainsi, le quadrilatère APBQ est un parallélogramme et D est le milieu de ses diagonales. On en déduit donc :

\( {\dfrac {\overline {\text{DB}}} {\overline {\text{DA}}} =-1.}\)

Comme R est « à l’infini » sur la droite (AB),  \( \overline{\rm RA}/\overline{\rm RB}=1.\)   On peut enfin en conclure que [A, B, D, R] = –1, ce qu’on se proposait de démontrer.

Au-delà de leur indéniable caractère esthétique, les théorèmes de Ménélaüs et de Ceva illustrent parfaitement que les différents types de géométrie (affine, projective, euclidienne…), loin de s’opposer, se complètent et s’enrichissent mutuellement.