D’un côté, on trouve les théorèmes mathématiques, à savoir des propositions démontrables qui résultent d’autres énoncés déjà démontrés ou admis sans preuve, comme les axiomes ou les postulats. D’un autre côté, la physique est une science qui étudie, par l’expérimentation et par l’élaboration de concepts, les propriétés fondamentales de la matière et de l’espace-temps ; une loi physique modélise et prévoit un phénomène naturel. En combinant les deux points de vue, une loi physique peut parfois « prouver » un résultat mathématique !

Trois points, c’est tout…

En 1636, le magistrat et mathématicien français Pierre de Fermat (vers 1601–1665) applique une technique analytique qu’il a développée, dite méthode de l’extremum, pour résoudre le problème suivant : Étant donnés trois points, en trouver un quatrième tel que la somme de ses distances aux trois points donnés soit la plus petite possible.

Quatre ans plus tard, le physicien et mathématicien italien Evangelista Torricelli (1608–1647) fournit une première réponse géométrique, en utilisant les propriétés des ellipses et en démontrant que le quatrième point devait être le point de concours de trois cercles (cercles qui, aujourd’hui, portent son nom).

À l’époque, les mathématiciens donnaient la seule position possible du quatrième point, mais ne prouvaient pas son existence. Aujourd’hui, on utiliserait la fonction qui associe à tout point la somme de ses distances à trois points fixes : l’existence du quatrième point découle de la continuité de cette fonction sur l’ensemble compact constitué de l’intérieur du triangle et de sa frontière.

Le problème a été popularisé pendant la Seconde Guerre mondiale sous la forme d’un problème voisin issu de la théorie des graphes et posé sur un arbre particulier, dit arbre de Steiner :

Quelle est la longueur minimale d’un réseau de communication devant connecter un certain nombre de points donnés ?

Partons maintenant à la recherche de F, le point de Fermat d’un triangle ABC (voir le Triangle, Bibliothèque Tangente 24, 2005 et le Cercle, Bibliothèque Tangente 36, 2009). On montre que si un angle au sommet du triangle mesure au moins 120° alors F s’y trouve. Chaque symétrie par rapport à un côté justifie que F ne soit pas à l’extérieur du triangle. 

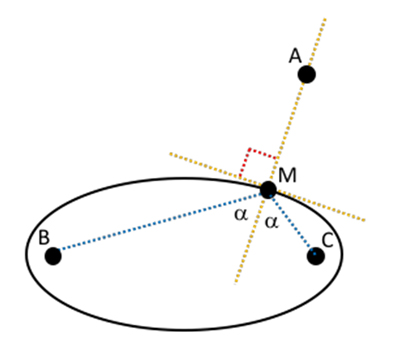
Sur une ellipse de foyers B et C dont l’intérieur ne contient pas A, la somme MB + MC est constante. Les points B et C étant fixes, MA + MB + MC est minimum lorsque MA est minimum, c’est-à-dire lorsque la droite (MA) est la normale à l’ellipse en M (dit autrement, perpendiculaire à la tangente au point M). D’après le théorème de Poncelet, la droite (MA) est la bissectrice intérieure de l’angle   \( \widehat {\text {BMC}}.\)

On raisonne de même sur B et sur C. Les angles  \( \widehat {\text {AMB}}\) et \( \widehat {\text {CMA}}\) , supplémentaires de α, sont égaux ; leurs moitiés, analogues à α, sont égales.

Ainsi, si le point cherché F existe, alors il est unique et vérifie que les angles  \( \widehat {\text {BFC}}, \widehat {\text {CFA}}\) et  \( \widehat {\text {AFC}}\) sont égaux à 120°.

De plus, F a le bon goût d’être constructible géométriquement. On trace les triangles équilatéraux CBA’, ACB’ et BAC’ à l’extérieur du triangle ABC. Les droites (BB’) et (CC’) font entre elles un angle  \( \widehat {\text {CTB'}}\) de 60° car B et B’ sont respectivement les images de C’ et de C par la rotation, dans le sens trigonométrique, de 60° autour de A.

Soit T le point d’intersection de ces droites. Les angles  \( \widehat {\text {CTB'}}\)  et  \( \widehat {\text {CAB'}}\) sont égaux (à 60°). D’après le théorème des angles inscrits (voir Tangente 178, 2017), T appartient au cercle circonscrit au triangle ACB’. On raisonne de même autour de B et de C. Les trois cercles circonscrits aux triangles équilatéraux sont concourants en T. Les angles \( \widehat {\text {CTA}}, \widehat {\text {ATB}}\) ,  et  \( \widehat {\text {BTC}}\)  valent chacun 120° : T n’est autre que F.

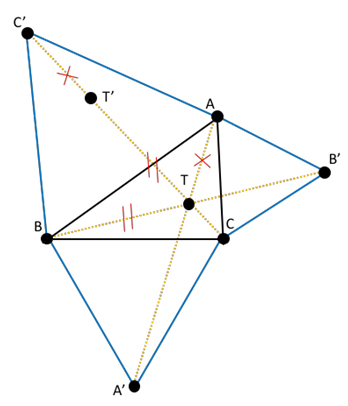
Soit T’ l’image de T par la rotation de 60° autour de B. Cette rotation conservant les distances, TA = T’C’. On montre que T’ appartient à la droite (CC’), puis que TB = TT’ dans le triangle équilatéral BTT’. On en déduit que TA + TB + TC = T’C’ + TT’ + CT = CC’. Ainsi, on peut visualiser directement le minimum de la fonction MA + MB + MC. Il s’agit tout simplement de CC’ (qui est alors aussi égal à BB’ et à AA’).

Avec l’énergie potentielle…

Le moment est venu de passer à une expérimentation. La loi de Dirichlet sur l’énergie potentielle et la troisième loi de Newton « prouvent » l’existence et la construction du point de Fermat–Torricelli dans le triangle !

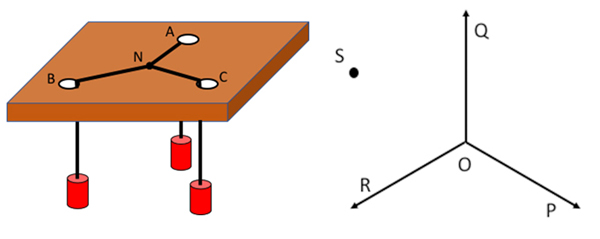
Sur une planche horizontale, on dessine un triangle ABC dont aucun angle n’excède 120° ; on va construire son point T (ou F). On perce un trou à chaque sommet du triangle. Par chaque trou, on fait passer une ficelle, à l’extrémité de laquelle on suspend un poids, toujours de la même masse m. On attache les trois ficelles en faisant un nœud N. Qu’observe-t-on ? Après divers mouvements, parfois surprenants, le système se stabilise. Le nœud N occupe précisément la position du point de Fermat–Torricelli.

Quelles explications la physique fournit-elle ? 

Selon le principe de Dirichlet, un système est en équilibre stable quand l’énergie potentielle de l’ensemble est minimale. Les seules forces s’exerçant sur le système, dirigées vers le bas, sont les poids. À une constante près, l’énergie potentielle d’un poids est m g h, où m est la masse, g l’accélération de la pesanteur et h l’altitude du point d’attache à la ficelle. La somme des altitudes des trois poids est minimale. Donc la somme des longueurs verticales des trois ficelles est maximale. Enfin, comme la somme des longueurs verticale et horizontale de chaque ficelle est donnée (constante), la somme des longueurs horizontales des trois ficelles NA + NB + NC est minimale.

Soient  \( \overrightarrow {\text {OP}}, \, \overrightarrow {\text {OQ}}\) et  \( \overrightarrow {\text {OR}}\) trois vecteurs de même norme et de somme nulle. Soit S le point tel que  \( \overrightarrow {\text {OS}} = \overrightarrow {\text {PO}}. \)

On a successivement :

\( \overrightarrow {\text {OS}} = \overrightarrow {\text {OQ}} + \overrightarrow {\text {OR}}\)   (traduction de la somme nulle),

\( \overrightarrow {\text {QS}} = \overrightarrow {\text {QO}} + \overrightarrow {\text {OS}} = \overrightarrow {\text {QO}} + \overrightarrow {\text {OQ}} + \overrightarrow {\text {OR}} = \overrightarrow {\text {OR}} \)  (par la relation de Chasles),

et de même  \( \overrightarrow {\text {RS}} = \overrightarrow {\text {OQ}}.\)

On en déduit que le quadrilatère OQSR est un losange et que OQS est un triangle équilatéral. Les angles  \( \widehat {\text {QOR}}, \, \widehat {\text {ROP}}\) et  \( \widehat {\text {POQ}}\)   mesurent 120°.

Selon la troisième loi de Newton, les forces exercées par les poids sont contrebalancées par des forces de tension dans chaque ficelle. Ces dernières, une fois répercutées en N, sont portées par les directions horizontales des trois ficelles. Elles peuvent être représentées par trois vecteurs de même norme et de somme nulle. D’après ce qui précède, les trois ficelles forment entre elles des angles de 120°.

Pythagore et la statique des fluides

On réalise un bac en verre ou en plexiglas, une sorte d’aquarium, dont la forme est un prisme droit. Le polyèdre est constitué de deux faces identiques parallèles, les bases, dont la forme est un triangle rectangle. Soient a et b les côtés de l’angle droit du triangle, c son hypoténuse. Le prisme est également constitué de trois faces latérales rectangulaires perpendiculaires aux bases.

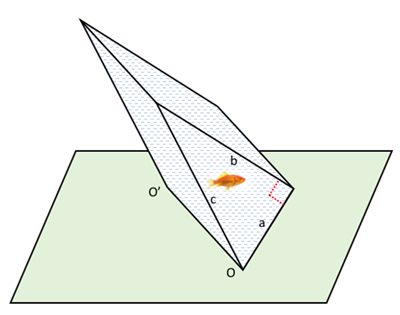
On remplit complètement le bac d’eau. On le pose sur une table, selon la hauteur (OO’) du prisme passant par le même angle aigu des triangles rectangles, par exemple celui entre les côtés a et c. Par analogie avec un solide, on pourrait s’attendre à ce que le bac d’eau « tombe » immédiatement… sauf à placer habilement son centre de gravité parfaitement à la verticale d’un point de (OO’). Mais ici, quelle que soit l’inclinaison du prisme par rapport au plan, le bac d’eau reste immobile : il ne glisse pas, et il ne tourne pas !

Là encore, quelles explications la physique fournit-elle ?

Sur chaque paroi, l’eau exerce une pression. Chaque force pressante s’exerce par unité d’aire ; la résultante de ces forces s’exerce à la perpendiculaire au centre de la paroi. Les aires des surfaces latérales sont proportionnelles au côté correspondant des triangles rectangles, l’autre dimension des rectangles étant la hauteur du prisme. Donc les intensités des résultantes des forces pressantes sur les parois latérales peuvent être écrites sous la forme ka, kb et kc, où k prend la même valeur pour toutes ces parois.

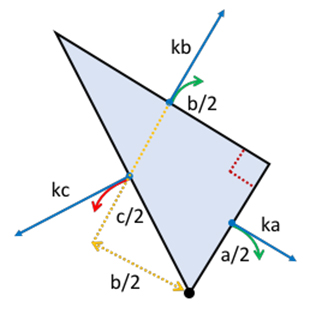
Le moment d’une force par rapport à (OO’), axe perpendiculaire au plan de la figure représenté par le petit disque noir en bas sur le dessin, est le produit de la distance du point d’appui de la force (a / 2, b / 2 ou c / 2) par l’intensité de sa composante tangentielle. Les moments des résultantes des forces pressantes par rapport à l’axe, orientés dans le sens des aiguilles d’une montre, sont ka  k / 2  = ka ² / 2, kb ² / 2 et –kc ² / 2. 

Comme le bac d’eau ne tourne pas autour de l’axe, les moments s’annulent : 

ka ² / 2 + kb ² / 2  kc ² / 2 = 0.

Après élimination du facteur k / 2, on retrouve le théorème de Pythagore : a ² + b ² = c ² !

Et si la base du prisme n’était pas un triangle rectangle, mais un triangle quelconque ? Qu’à cela ne tienne : soit α l’angle entre les côtés a et b. La distance de point d’appui b / 2 devient b / 2 – a cos α.

L’annulation des moments donne alors :

ka ² / 2 + kb (b / 2 – a cos α) – kc ² / 2 = 0.

Après élimination du facteur k / 2, on retrouve la formule d’al-Kashi, ou loi des cosinus :

a ² + b ² – 2ab cosα = c ² !