Pourquoi s’obstiner à faire une distinction entre «  mathématique pure » et « mathématique appliquée » quand chacune a régulièrement des incidences positives sur l’autre ? Un bel exemple nous en est donné par le problème des trois corps en mécanique céleste. Son histoire est aussi celle de la revue spécialisée Acta Mathematica, fondée en 1882 par le mathématicien suédois Gösta Mittag-Leffler. En 1889, afin d’en asseoir le prestige, ce dernier voulut profiter des festivités organisées pour la célébration du soixantième anniversaire du roi Oscar II de Suède, lui-même amateur de mathématiques, qui proposait d’offrir pour l’occasion un prix substantiel à qui apporterait la solution à un problème important.

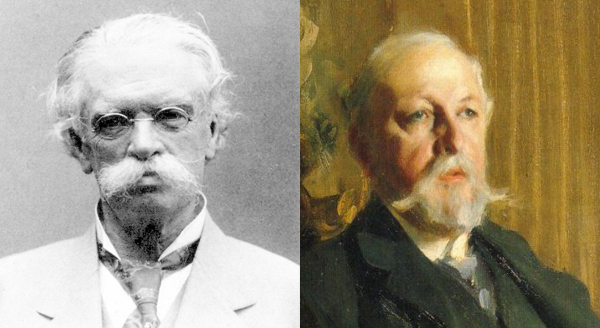
Gösta Mittag-Leffler (1846–1927).       Le roi Oscar II de Suède et de Norvège (1829–1907). 

Un manuscrit mis au pilon

Répondant à cette invitation, Henri Poincaré proposa un mémoire de cent soixante pages intitulé Sur le problème des trois corps et les équations de la dynamique. Le prix lui fut attribué à l’unanimité du jury et son mémoire mis sous presse. Mais les choses se compliquèrent. Mittag-Leffler avait chargé le jeune mathématicien Lars Phragmén de relire attentivement le mémoire de Poincaré. Des réserves pertinentes furent mises au jour sur certains résultats du Français. Preuve de son intelligence supérieure, Poincaré reconnut ses erreurs et en assuma les responsabilités financières en remboursant tous les frais inhérents à la publication du premier mémoire, qui dut être mis au pilon ! Le travail initial, malgré les erreurs, demeure plus qu’intéressant du point de vue des mathématiques : il contient entre autres le fameux théorème de récurrence de Poincaré, qui est l’acte fondateur de la théorie ergodique (ou étude des systèmes dynamiques mesurés). Ce théorème affirme, sous certaines hypothèses raisonnables (voir FOCUS "Le théorème de récurrence de Poincaré), que pour « un très grand nombre » de conditions initiales, tout système dynamique va repasser au cours du temps aussi près que l’on veut de sa condition initiale, et ce de façon répétée.

  Jules Henri Poincaré (1854–1912).                          Lars Edvard Phragmén (1863–1937).

L’évolution des systèmes dynamiques est souvent décrite à partir d’équations différentielles. C’est le cas de la loi de gravitation universelle, selon laquelle la force d’attraction entre deux corps est proportionnelle à chacune des masses et inversement proportionnelle au carré de leur distance. Qui dit force, dit accélération, et donc dérivée seconde de la position. Dans le cas du système solaire, les n corps célestes sont assimilés à autant de masses ponctuelles. La résolution de l’équation différentielle associée nécessite la donnée des positions (trois dimensions) et des vitesses (trois dimensions également) des n corps au même instant t.

L’espace des états possibles (appelé espace des phases) possède donc 6n dimensions. Quand on ne prend en considération que deux corps, dont l’un est significativement plus massif que l’autre, la résolution de l’équation est connue (voir les précédents articles de ce dossier) : le « petit » corps décrit, relativement à l’autre, une ellipse dont le « gros » corps est un foyer.

Que se passe-t-il quand on considère plus de deux corps ?

Une vision géométrique

La plupart des mathématiciens avant Poincaré s’attelaient à résoudre les équations différentielles en restant dans le champ de l’analyse, quitte à en proposer des solutions au moyen de formules de plus en plus sophistiquées. Poincaré s’aperçut que l’obtention de formules exactes était le plus souvent impossible. Il changea de point de vue en traitant les solutions des équations différentielles comme des objets géométriques. Il se concentra sur le problème des trois corps, en supposant que celui dont il entendait décrire la trajectoire avait une masse nulle (m = 0), tout en subissant l’attraction des deux autres, de masses respectives m₁ et m₂. En postulant que les trajectoires des trois masses se situaient dans le même plan, Poincaré réduisait l’espace des états possibles à la dimension 4 : position et vitesse initiales de la masse m dans ce plan.

Dans l’espace des phases, l’ensemble des conditions initiales associées à m va être représenté par une famille de courbes engendrant une hypersurface S de dimension 3, chacune de ces courbes correspondant à un certain niveau d’énergie supposé invariant (son hamiltonien). Les équations d’évolution induisent alors une transformation T des courbes de cette hypersurface sur elle-même, d’où le point de vue géométrique.

Poincaré postule ensuite que le rapport r des deux masses m₁ et m₂, qui influencent m, est négligeable. Il se place dans un système plan dans lequel le corps m₁ est immobile à l’origine, et dans lequel le corps m, ne subissant pas d’attraction de m₂, décrit une ellipse dont m₁ est un foyer. Dans ce cas particulier, le système est complètement intégrable (c’est-à-dire, pour simplifier, que les trajectoires des corps sont périodiques ou quasi périodiques).

Que se passe-t-il si le rapport r cesse d’être négligeable ?

Les points d’équilibre

Poincaré se concentre sur les orbites périodiques, suivant une trajectoire invariante par T lorsque le rapport r tend vers 0. Quand r est « petit » mais non nul, il découvre que seul un nombre fini de points demeurent fixes sous la transformation T et correspondent toujours à des orbites périodiques. Pour comprendre la situation, on peut proposer une analogie avec un pendule. Sans gravitation et sans frottement (cas correspondant à r = 0), une barre rigide fixée à l’une de ses extrémités et mise en mouvement présentera un mouvement de rotation uniforme. Toutes ses positions seront des positions d’équilibre, auxquelles la barre reviendra après un temps fini. Par contre, en présence de la moindre force de pesanteur, même très petite, cette barre mise en mouvement tendra vers deux positions : barre vers le bas (équilibre stable) ou barre vers le haut (équilibre instable), « haut » et « bas » constituant une terminologie relative à la force de pesanteur exercée.

À gauche : Le pendule tend vers la position d’équilibre stable.
À droite : À la moindre perturbation, le pendule quitte la position d’équilibre instable.

La nature de l’erreur

Ce comportement est alors qualifié de doublement asymptotique par Poincaré. Cette appellation, à laquelle on préfère aujourd’hui celle d’homocline, s’explique en étudiant les points fixes instables (équivalents de la barre vers le haut). Poincaré constate que pour chaque point fixe x il existe une courbe de S, passant par x, telle que tout point de la courbe auquel on applique T engendrait une suite de points convergeant vers x. Cette courbe est qualifiée de stable ou positivement asymptotique. De façon symétrique, il existe une courbe négativement asymptotique jouissant de la même propriété pour la transformation inverse T ^–1. Dans le cas de la barre rigide en rotation, ces deux courbes coïncident.

Revenant au cas des trois corps, Poincaré s’attèle à déterminer les positions des courbes positivement et négativement asymptotiques, en effectuant des développements en série relativement aux puissances de r ^1/2. La première version du mémoire démontrait que les deux courbes coïncidaient au premier ordre en r ^1/2 et supposait que les deux développements convergeaient, et que cette convergence assurait l’identité des deux courbes.

La version corrigée est beaucoup plus subtile ! Le mathématicien lorrain y vérifie la coïncidence des deux courbes à tous les ordres du développement. Mais il démontre également, dans la foulée, la non-convergence des développements. Tout au plus peut-il affirmer que les courbes positivement et négativement asymptotiques se coupent en des points distincts des points fixes auxquels elles sont associées… Il constate de plus que les tangentes en ces points d’intersection sont généralement distinctes. Ces points d’intersection correspondent à ce que l’on nomme aujourd’hui des trajectoires homoclines transverses. La recherche, en dehors de tout contexte physique, de ces courbes positivement et négativement asymptotiques présentant ces intersections homoclines transverses constitue un nouveau pan de la géométrie d’une complexité redoutable.

Le système solaire « chaotique »

Les conséquences de la découverte de Poincaré ont bouleversé notre conception du système solaire. Il était jusque-là admis que ce dernier était stable. Henri Poincaré montra que les équations de la dynamique céleste dissimulaient un chaos potentiel ! Mais qu’en était-il de notre système et de notre planète Terre ? Un siècle après les travaux de Poincaré, l’astronome français Jacques Laskar démontra (en 1989) que toutes les planètes du système solaire avaient des courses « chaotiques ». Mais cette constatation ne doit pas nous inquiéter : pour ces systèmes, on introduit la notion d’horizon de Lyapounov, qui quantifie la durée au-delà de laquelle toute prédiction d’un système dynamique donné devient impossible. L’horizon de Lyapounov de notre système solaire est de plusieurs dizaines de millions d’années…

Poincaré était conscient du côté partiel de ses résultats. Dans l’introduction à son mémoire, il nota : « Je suis bien loin d’avoir résolu complètement le problème que j’ai abordé. Je me suis borné à démontrer l’existence de certaines solutions particulières remarquables que j’appelle solutions périodiques, solutions asymptotiques et solutions doublement asymptotiques. » Malgré ses doutes, le mathématicien français avait ouvert la voie de la théorie du chaos, qui allait livrer quantité de résultats intéressants au XX^e siècle.