Le mathématicien suisse Johann Bernoulli, analysant un manuscrit rendu anonyme proposant une solution au problème de la courbe brachistochrone, identifia l’auteur à Isaac Newton. Il aurait eu ce commentaire : « Ex ungue leonem » (« on reconnaît le lion à sa griffe »).

Sans doute le plus grand succès du Vieux Lion, alors rugissant en 1685, est la parution de son œuvre maîtresse Philosophiae naturalis principia mathematica (« principes mathématiques de la philosophie naturelle »). Il applique en particulier sa méthode pour résoudre le fameux problème des deux corps, qui préoccupe les savants de l’époque : quelle est l’évolution, dans le temps, de deux corps A et B en interaction mutuelle, assimilés à des points matériels, le système global {A, B} étant considéré isolé du reste du monde ? Ainsi, si notre satellite reste bien en orbite autour de la Terre, il possède de très nombreux mouvements « parasites », que l’on a du mal à décrire. C’est tout l’objet du problème des deux corps !

Newton et les deux corps

Dans le problème d’astronomie du mouvement de B autour de A dans le système de référence (A, x, y, z) résolu par Newton, six constantes du mouvement apparaissent :

• deux décrivent la nature et la forme de la conique contenant le mouvement : le demi-grand axe a > 0 et l’excentricité e > 0 ;

• deux sont des angles permettant de définir le plan dans lequel s’effectue le mouvement par rapport à un système de référence (A, x, y, z) donné : la longitude du nœud ascendant Ω et l’inclinaison du plan orbital i ;

• deux permettent de positionner le point B sur son orbite à l’instant t : l’argument ω du périastre P et l’instant τ du dernier passage en ce point.

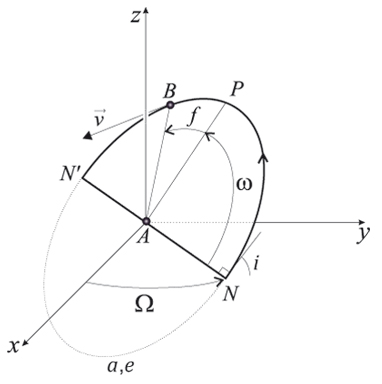
               Les paramètres astronomiques. 

Dans le cas où B est la Lune, le point A est bien sûr la Terre, l’axe (Ax) correspond à la direction du point vernal (intersection entre les plans de l’équateur terrestre et de l’écliptique, voir les Angles, Bibliothèque Tangente 53, 2015). Les six constantes ne le sont effectivement que dans le cadre du problème théorique de Newton entre deux masses ponctuelles et isolées. Dans la réalité, on observe depuis très longtemps des mouvements autour de cette situation académique. Dans le cas de notre satellite naturel, ils sont recensés depuis l’Antiquité :

1. La ligne (NN’) reliant les points où la trajectoire coupe le plan (Axy) de référence tourne dans ce plan autour de A avec une vitesse à peu près constante n _Ω proche de 19° par an. Si bien qu’en dix-huit ans et un peu plus de sept mois cette ligne fait un tour complet ;

2. La direction (l’axe (AP)) de son périgée (le point de l’orbite où B est le plus proche de A, voir l’Astronomie, Bibliothèque Tangente 21, 2004) tourne dans le plan orbital d’un peu plus de n_ω, environ 40°, par an, si bien qu’en neuf ans et quelques mois il revient au même endroit (dans ce plan).

Trois autres de ces « constantes », a, e et i, le sont bien mais uniquement « en moyenne dans le temps ». Le cas de τ est un peu particulier…

On connaissait donc tout cela au milieu du XVIII^e siècle mais on ne pouvait l’expliquer. On se doutait bien que le mouvement de la Lune n’était pas seulement dû à la Terre : la force de gravitation que lui impose le Soleil est du même ordre de grandeur que celle dont la Terre est à l’origine. Mais on ne savait pas résoudre ce problème, qui devenait donc à trois corps.

La méthode utilisée par Newton pour venir à bout du problème à deux corps est géométrique. Mais elle repose par ailleurs sur une symétrie tout à fait particulière de ce problème : la conservation du vecteur de Hamilton \( \overrightarrow{{h}} \) . La méthode introduite par Newton tombe donc avec l’absence de cette propriété.

Des fonctions liées à leurs dérivées

Pour envisager une réforme de la méthode introduite par Newton, il a fallu comprendre la portée mathématique de sa définition de la force. Si la vitesse d’un corps varie au cours du temps, ses composantes dans un référentiel donné deviennent des fonctions du temps. Cette notion de fonction est d’ailleurs introduite par Leibniz à la même époque. C’est par contre un Britannique, l’Écossais Colin MacLaurin, qui viendra en 1741 expliquer que le cadre instauré par Newton impose à ces fonctions de vérifier de bien curieuses équations qui les relient à leurs dérivées. Alors que jusque-là les équations des mathématiciens avaient pour solution un nombre, ou un ensemble de nombres, le modèle émergent en physique faisait apparaître des équations différentielles, ayant pour solution des fonctions. La suite est l’affaire de l’un des plus grands mathématiciens de l’histoire, Joseph-Louis Lagrange.

 Colin MacLaurin (1698–1746).                        Joseph-Louis, comte de Lagrange (1736–1813).

Comme souvent face à un nouveau problème, on va s’intéresser aux situations « les plus simples » afin de tenter de les comprendre pour espérer les généraliser. Le jeune Piémontais, né Giuseppe Lodovico de Lagrangia, cherche donc à déterminer une fonction f₀ dont la dérivée f₀’ serait le produit de f₀ par une fonction connue p qui jouerait le rôle d’un paramètre dans cette équation. Et il la trouve lorsque la fonction p est ce que l’on appelle une « fonction » à cette époque (c’est-à-dire quelque chose de « lisse et régulier ») :  f₀ = λ exp(P) où λ est une constante quelconque et P une fonction dont la dérivée est p. Dans toutes ces expressions, on n’a pas besoin de faire apparaître la variable de la fonction cherchée : l’inconnue de l’équation est une fonction !

La notation f ’ pour la dérivée de f est introduite à cette occasion par Lagrange.

On vérifie aisément que la solution proposée convient, en sachant que (λ f )’ = λ f ’ car λ est une constante et que (exp(P))’ = P’  exp(P) = p exp(P) car la fonction exponentielle est, par définition, sa propre dérivée.

Ce premier problème résolu, Lagrange le complique en introduisant une nouvelle « fonction paramètre » q au second membre de l’équation différentielle précédente, qui devient  f₁’ = p f₁ + q. L’équation est dite perturbée. Ce problème est lui aussi résolu dans la même publication, Sur l’intégration d’une équation différentielle à différences finies, qui contient la théorie des suites récurrentes. Il montre que la solution du problème s’écrit sous la forme  f₁ = G f₀ + q, où la fonction G est telle que sa dérivée g vérifie la relation g  f₀ + q ’ = (p + 1) q. Dans cette expression « 1 » désigne la fonction partout égale à l’unité. La relation permettant de déterminer G n’est plus une équation différentielle, il s’agit (comme on le dirait maintenant) d’un calcul de primitive. Le problème est donc résolu.

Pour trouver la solution de l’équation différentielle perturbée par un second membre, il convient donc, à la fonction (connue) q près, de remplacer la constante λ du problème non perturbé par une fonction G dont la dérivée sera déterminée : c’est ce que Lagrange appelle la méthode de variation de la constante. Cette méthode analytique de résolution de problème mathématique, encore utilisée et enseignée partout de nos jours, est radicalement différente de la méthode synthétique basée sur la géométrie : on utilise ici uniquement des règles de dérivation, d’addition et de multiplication sur des éléments abstraits que sont les fonctions.

Des constantes qui varient…

Revenons à notre problème des trois corps : le mouvement de la Lune autour de la Terre, perturbé par le Soleil. Dans le référentiel (A, x, y, z), la position de la Lune est définie par le vecteur  \( \overrightarrow{r} \) de composantes (x, y, z) et par sa vitesse  \( \overrightarrow{v} \) de composantes (v_x, v_y, v_z). Tous ces paramètres sont des fonctions du temps ; ils vérifient les équations différentielles suivantes :

x ’ = v_x,

y ’ = v_y,

z ’ = v_z,

\( v'_x= \dfrac{x}{r^3} + \text{F} _x,\)

\( v'_y= \dfrac{y}{r^3} + \text{F} _y,\)

\( v'_z= \dfrac{z}{r^3} + \text{F} _z.\)

Le vecteur  \( \overrightarrow{\text{F}} \) de composantes ( F_x, F_y, F_z ) décrit la perturbation, supposée connue, induite par le Soleil sur le mouvement de la Lune située à une distance \( r= \sqrt{x^2 + y^2 + z^2}\)  de la Terre.

Sans perturbation, ces six équations font apparaître six constantes, que l’on peut rassembler dans un vecteur  \( \overrightarrow{\text{C}} \) = (a, e, i, ω, Ω, τ). Pour trouver la solution du problème perturbé, Lagrange propose donc de faire « varier ces constantes », en appliquant sa méthode. Le problème, qu’il soulève d’emblée, est que cette idée ne devra rester que préliminaire car, contrairement au cas simple traité exactement dans le cas général, les équations du problème des deux corps perturbé ne sont pas linéaires. La méthode ne s’applique donc pas ! Mais qu’à cela ne tienne : Lagrange ose l’appliquer tout de même, en cherchant l’inspiration. Les composantes constantes de  \( \overrightarrow{\text{C}} \) deviennent des fonctions, le vecteur devient donc \( \overrightarrow{\text{C}} \) (t) = (a (t), e (t), i (t), ω (t), Ω (t), τ (t)) et ses composantes vérifient un système d’équations différentielles qu’il peut mettre sous la forme  \( \overrightarrow{\text{C'}} = \text{L} \,\overrightarrow{\text{grad} _{\overrightarrow{\text{C}}} (\text{R})}\) (voir FOCUS "La notion de gradient"). 

La matrice L est antisymétrique et la force  \( \overrightarrow{\text{F}} \) doit dériver d’une fonction perturbatrice, \( \overrightarrow{\text{F}} = \overrightarrow{\text{grad} _{\overrightarrow{r}} (\text{R})}\) ,
qui ne doit elle-même dépendre que de la position :  \( \text{R} = \text{R} (\overrightarrow{r} ). \) Tout ceci semble bien compliqué, mais le jeune mathématicien parvient à montrer (d’une part) qu’en moyenne temporelle a (t), e (t) et i (t) sont bien des fonctions constantes, et (d’autre part) que Ω’ = F ( a, e, i  ) et ω’ = G ( a, e, i ).

Bien que sophistiquées, les fonctions F et G sont explicites. Évaluées au point constant ( a, e, i ), elles fournissent la valeur, constante, de la variation temporelle des fonctions Ω et ω sous l’action de la perturbation. Les applications numériques sont saisissantes : pour la ligne des nœuds de la Lune perturbée par le Soleil, on trouve F (a, e, i ) « proche » de n _Ω et, pour son périgée, G (a, e, i ) « proche » de n_ω / 2. Les valeurs de n _Ω et n_ω sont précisément celles observées depuis longtemps !

Hormis donc le facteur 2 indélicat, Lagrange reproduit, avec sa théorie de la variation des constantes lunaires, toutes les observations centennales sur notre satellite. Il reçoit pour ces travaux le Grand Prix de l’Académie des sciences de Paris en 1764. Quel succès pour une théorie qui ne devait même pas s’appliquer !

Vers le calcul des variations

En cherchant à comprendre ce qu’il devait conserver de ce succès inattendu, Lagrange retient qu’il est bien plus utile de s’intéresser aux champs dont elles dérivent qu’aux forces elles-mêmes, qui ne sont en fait qu’une étape provisoire dans l’écriture d’un modèle efficace. En généralisant de manière rigoureuse cette méthode, il parvient à formuler une méthode complètement analytique pour l’étude des problèmes de mécanique. Le grand Leonhard Euler, émerveillé par ces résultats, comprendra que l’on peut associer un principe de moindre action à tout ceci : la géométrie synthétique de Newton laisse alors la place à l’analyse et au calcul variationnel. À la fin de sa vie, vers 1813, stimulé par son brillant étudiant Siméon Denis Poisson, Lagrange écrit les équations générales du mouvement d’un système non dissipatif sous une forme équivalente à celle obtenue pour les mouvements planétaires, qui fait intervenir les énergies cinétique T et potentielle V du système considéré :

\( \overrightarrow{\text{Z'}} = \text{J} \,\overrightarrow{\text{grad} _{\overrightarrow{\text{Z}}} (\text{H})}\)   avec   \( \overrightarrow{\text{Z}} = (\overrightarrow {r} \,\,\, \,\,\, \overrightarrow {p}), \)    \( \overrightarrow {p}= m \overrightarrow {v}, \)

H = T +V et

  \( \text{J} = \begin{pmatrix} 0 & \text{I}_d \\ -\text{I}_d & 0 \end{pmatrix}.\)

Ces travaux seront publiés de manière posthume en 1814. Le travail de compilation est effectué par un autre de ses élèves, Jacques Philippe Marie Binet (1786–1856). La lettre H avait été introduite par Lagrange en mémoire à Huygens, qui avait, selon lui, compris l’importance des quantités conservées dans les problèmes de mécanique.

Leonhard Euler (1707–1783).                            Sir William Rowan Hamilton (1805–1865).

Presque trente ans plus tard, un autre mathématicien, William Hamilton, traduira en anglais cette œuvre magistrale, que l’Irlandais désigne sous le nom de « poème scientifique rédigé par le Shakespeare des mathématiques ». C’est ainsi qu’en suivant Hamilton en anglais plutôt que l’original du maître, Paul Dirac proposera en 1927 d’appeler hamiltonien ce H que Lagrange avait dédié à Huygens. Les équations portent aussi le nom de l’Irlandais qui n’avait pourtant que 5 ans au moment où notre Français, naturalisé par Napoléon, avait tout écrit et expliqué.