Les nombres complexes de module 1

Il est souvent difficile de cerner l'apport des divers contributeurs d'un concept. Comme disait Farkas Bolyai, pour presser son fils János de rédiger au plus vite ses idées sur la géométrie non euclidienne :

« Quand le temps est mûr pour certaines choses, celles-ci apparaissent en divers endroits un peu comme des violettes qui éclosent au début du printemps. »

La notion de nombre complexe ne déroge pas à ce constat. Ainsi, le Danois Caspar Wessel (1745–1818) fut le premier à proposer une interprétation géométrique des imaginaires dans son traité Essai sur la représentation analytique de la direction en 1799. Mais, par sa vision mathématique, ses démonstrations illustrées par des figures géométriques, l'« Essai » de Jean-Robert Argand en 1806 peut être considéré comme le texte fondateur de la représentation géométrique des nombres complexes.

  
Des racines primitives

Les coordonnées polaires sont particulièrement bien adaptées pour les nombres complexes. À un point M du plan réel de coordonnées (r cos ( \( \theta\) ), r sin ( \( \theta\) )), on fait correspondre dans le plan complexe l'affixe z = r (cos ( \( \theta\) )+i sin ( \( \theta\) )), où r est le module et u un argument de z. En 1748, Euler utilise pour la première fois l'écriture exponentielle, qui facilite grandement tous les calculs multiplicatifs. Cette notation éclaire la similitude associée à la multiplication par le nombre complexe z  = re^{i \( \theta\)} . C'est la composition, avec l'origine pour centre, d'une homothétie de rapport r et d'une rotation d'angle  \( \theta\) .

Un nombre complexe de module 1 est ainsi associé à un point M du cercle trigonométrique, de centre l'origine O et de rayon unité, et entièrement défini par son argument  \( \theta\) , angle entre l'axe des abscisses et le vecteur  \( \overrightarrow{\text{OM}}\) . Il est caractérisé par le fait d'avoir son conjugué égal à son inverse : \( \bar{z}=e^{-i\theta}=z^{-1}\) . L'ensemble des nombres complexes de module 1, stable par la multiplication, constitue un groupe multiplicatif, noté U.

L'équation complexe zⁿ = 1 possède n racines d'après le théorème fondamental de l'algèbre. La somme de ces racines, opposée au coefficient du terme en z^n–1, est nulle. Une solution complexe    z  = re^{i \( \theta\)}  (en notation exponentielle) est donc telle que rⁿ = 1  et n \( \theta\)  = 2k \( \pi\)  , avec k un entier. 

On appelle racines de l'unité les n nombres complexes  \( \omega_{n, k}= e^{{{i}{\frac{2\pi k}{n}}}}\) de module 1 (pour k allant de 0 à n – 1), que l'on peut écrire \( \omega_{n, k}= \rho^k_n\) , en notant

\( \rho_n=\omega_{n, 1}=e^{ {i}{\dfrac{2\pi}{n}} }\) .

On a donc la factorisation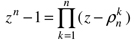

\( z^{n}-1=\prod\limits_{k=1}^n (z-\rho_n^k).\)

Les racines n^èmes de l'unité constituent un groupe cyclique U_n d'ordre n pour la multiplication des nombres complexes (voir en encadré). De façon générale, si p est multiple de n (donc si p = m  n), une racine n^ème de l'unité est racine p^ème de l'unité puisque z ^p = (z ⁿ)^m = 1 .

On appelle alors racine primitive n^ème de l'unité, ou d'ordre n, un nombre complexe z tel que n est le plus petit entier vérifiant zⁿ = 1. Ainsi, parmi les racines de l'équation \( z^4=1\) , \( \omega_{4,0}=1\)  est d'ordre 1,  \( \omega_{4,2}=\omega_{4,1}^2=-1\)  est d'ordre 2, et \( \omega_{4,1}=i\)  et  \( \omega_{4,3}=i^3=-i\)  sont d'ordre 4.

Pour z ³ = 1, les racines sont  \( \omega_{3,0}=1\) ,  \( \omega_{3,1}=j\)  et  \( \omega_{3,2}=j^2\) , avec j, et donc son conjugué j², racines primitives d'ordre 3.

Puisque  \( \omega_{n, k}= \rho^k_n\)   pour toute racine n^ème de l'unité, le complexe \( \rho_n\)  est un générateur du groupe cyclique U_n, dans tous les cas. Mais pour qu'une racine n^ème soit un générateur de U_n, il faut que son ordre soit n, c'est-à-dire qu'elle soit une racine primitive n^ème de l'unité. En conclusion, les générateurs de U_n sont les racines de l'unité  \( \rho^k_n\)  avec k premier avec n. Leur nombre est donc donné par la fonction indicatrice d'Euler \( \phi(n)\) (voir en encadré).

Ainsi, puisque \( \phi\) (4) = 2, U₄ n'admet que deux générateurs : \( \rho\)  ₄ = i  et  \( \rho_4^3\)    =   – i. En effet, nous avons vu que  \( \rho\)  ₄ est générateur, et nous avons

U₄ = {1, \( \omega_{4,3}\)  , \( \omega_{4,3}^2\)  , \( \omega_{4,3}^3\)  }

puisque 

\( \omega_{4,3}^2\)  = ( –i)² =  \( \omega_{4,3}\)  et  \( \omega_{4,3}^3\)  = ( –i)³ =  \( \omega_{4,1}\) .

De plus, cette caractérisation des racines de l'unité par leur ordre permet de déterminer les sous-groupes. Ainsi, U₄ admet pour sous-groupe le groupe C₂, d'ordre 2, de générateur

\( \omega_{4,2}\)  =  –1 : C₂ = {  \( \omega_{4,0}\) ,  \( \omega_{4,2}\)  } = {1, –1}.

Les polynômes cyclotomiques

Les racines de l'unité se répartissent régulièrement sur le cercle trigonométrique. Cette notion de découpe (tomos) du cercle (kyklos) se retrouve étymologiquement dans le terme « cyclotomique », associé à des polynômes qui sont historiquement apparus avec la construction des polygones réguliers à la règle et au compas. Le sens de ce terme est mis explicitement en évidence par le terme allemand Kreisteilungspolynom.

On a remarqué que

\( X^{n}-1=\prod\limits_{k=1}^n (X-\rho^k).\)

En ne conservant que les racines primitives, on obtient un polynôme, dit cyclotomique, diviseur du polynôme Xⁿ – 1, qui a pour expression

\( \Phi_n(X)=\prod_{\substack{k=1 \\ k \wedge n=1}}^n (X-\rho^k).\)

en notant k _^ n le plus grand commun diviseur de k et de n. Si k _^ n = 1, les nombres entiers k et n sont premiers entre eux.

Avec cette définition, on établit une factorisation du polynôme

\( X^n-1=\prod\limits_{d | n}\Phi_d (X),\)

où le produit s'effectue pour tous les diviseurs d de n. Puisque le degré du polynôme  \( \Phi_k(\text {X})\)  est \( \phi(k)\) , on obtient, à partir de cette égalité entre polynômes de degré n, la remarquable relation arithmétique suivante :

\( n=\sum\limits_{d | n}\phi (d).\)

 Si n est premier, ses seuls diviseurs sont 1 et n et donc

  \( \text{X}^n-1= \Phi_1(\text {X})\Phi_n(\text {X})\) . 

Puisque 

\( \Phi_1(\text{X})=\text{X}-1\) , 

on a

\( \Phi_n(X)=\frac{X^n-1}{X-1}=X^{n-1}+X^{n-2}+\ldots+X+1\)

Les premiers polynômes cyclotomiques sont :

• \( \Phi_2(\text{X})=\text{X}+1\) , puisque 2 est premier ;
générateur r ₂ =  –1 ;

• \( \Phi_3(\text{X})=\text{X}^2+\text{X}+1\) , puisque 3 est premier ;
générateurs j et j² ;

• \( \Phi_4(\text{X})=\text{X}^2+1\)  ; générateurs i et – i ;

• \( \Phi_6(\text{X})=\Phi _3 (\text{-X}) = \text{X}^2-\text{X}+1\)  ;
générateurs –j et –j².

Tous ces polynômes sont à coefficients entiers et irréductibles sur ℚ, c'est-à-dire ne peuvent être mis en facteur.

En étudiant, en digne héritier de Lagrange, les permutations des racines des polynômes cyclotomiques, Gauss crée les germes de la théorie des groupes de Galois. Il crée une nouvelle branche mathématique, la théorie algébrique des nombres, en construisant les entiers de Gauss à partir du polynôme cyclotomique  \( \Phi_4(\text{X})=\text{X}^2+1\) .