Un nombre complexe, c'est quoi ?

Les nombres complexes, on l'a compris, sont issus de la volonté d'accéder à une résolution des équations algébriques (annulation d'un polynôme), et plus particulièrement des équations du second degré.

Le nombre i, un symbole

Le point de blocage, qui a mis des siècles à être accepté, est la résolution de l'équation, pourtant élémentaire, X² = -1. Elle a donné naissance à la création de i, ce nombre appelé « imaginaire » car impossible à rattacher aux nombres « réels » qui constituaient jusque là l'environnement universellement admis du calcul algébrique.

Le séisme peut être comparé à la révolution qui a secoué l'école pythagoricienne quand l'existence des nombres irrationnels a été mise à jour.

Le nombre i est le symbole d'une nouvelle approche des mathématiques. Il permet dans un premier temps de résoudre l'ensemble des équations de degré 2 à coefficients réels en mettant en évidence deux racines, même quand le discriminant est négatif (voir encadré). 

Les racines d'une telle équation s'écrivent de manière unique sous la forme z = a + i b, où a et b sont des nombres réels. La tentation est grande d'inventer un ensemble, qui sera noté  $\mathbb{C}$ (comme « complexe »), somme d'un réel (sa « partie réelle ») et du produit de i par un autre nombre réel (sa « partie imaginaire »).

Dans cet ensemble, on peut étendre les opérations classiques des réels.

L'addition :

(a + i b) + (a' + i b') = (a + a') + i (b + b') 

les parties réelles, comme les parties imaginaires s'ajoutent.

La multiplication : 

(a + i b)  $\times$ (a' + i b') = (aa' – bb') + i (ab' + a'b).

Ces deux opérations possèdent dans $\mathbb{C}$ les mêmes propriétés que dans $\mathbb{R}$ , ce qui donne à $\mathbb{C}$ ce qu'on appelle une structure de corps.

On peut même créer une autre opération, la multiplication par un scalaire (en l'occurrence un réel) qui permet d'y ajouter la structure d'espace vectoriel de dimension 2, dont une base est formée du couple (1 ; i).

La représentation d'un complexe

Les réels ont été très vite représentés sur un axe orienté à l'origine duquel est placé 0. Compte tenu de leur dimension 2, il était donc naturel de chercher à représenter les complexes sur un plan muni d'un repère : une origine O (où est localisé 0) et deux axes, l'axe des réels et celui des imaginaires. Et si ce plan est affecté de la norme euclidienne qui fait de 1 et i une base de vecteurs orthonormés, de remarquables propriétés surgissent !

Au point qu'à l'inverse, pour résoudre certains problèmes de géométrie, on utilise le procédé inverse. On affecte chaque point du plan euclidien de son affixe, le complexe qui le représente, et on utilise les propriétés géométriques qui découlent de la représentation des complexes.

Comme le dossier sur les représentations géométriques le montre, ces propriétés créent des relations entre les points et les nombres, mais aussi entre les transformations de ces points et les opérations sur les nombres.

Ainsi, deux nombres conjugués z = a + i b et $\overline{z}$  = a - i b sont représentés par des points M et M' symétriques par rapport à l'axe des réels. Mais, chose étonnante, leur produit  $z$ $\overline{z}$  est égal à a² + b² = |z|², carré de la norme de z (ou de  $\overline{z}$ ), c'est-à-dire de la distance OM (ou OM'). On appelle également cette norme le module de z.

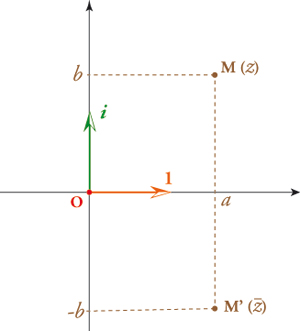Ce module vérifie l'inégalité classique d'une norme : |z + z'| ≤ |z| + |z'|, ce qui est la moindre des choses. Moins évidente est la relation liée au produit : |z . z'| = |z| . |z'|, qui se démontre assez facilement en étudiant les carrés des normes.

Cette représentation dans un plan euclidien permet aussi d'introduire la notion d'angle. Au lieu de se contenter de l'abscisse et de l'ordonnée du point M représentant un nombre complexe z = a + i b, on peut introduire le module r = |z| (déjà évoqué) et l'argument $\theta$  qui est l'angle orienté formé par les vecteurs 1 et $\overrightarrow{\text{OM}}$ .

En utilisant les définitions classiques des fonctions trigonométriques, on peut alors écrire z sous la forme : z = r (cos $\theta$  + i sin  $\theta$ ).

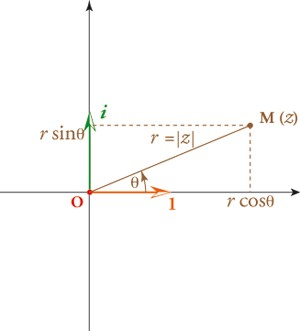Mais surgissent alors des résultats saisissants dont un certain nombre de conséquences seront développées dans les deux autres dossiers de ce numéro consacrés à la géométrie et à la trigonométrie.

Ainsi, en faisant le produit de deux complexes :

z = r (cos  $\theta$  + i sin  $\theta$ ) et z' = r' (cos  $\theta$ ' + i sin  $\theta$ '),

on trouve :

z z' = r r' [(cos  $\theta$   cos  $\theta$ '  – sin  $\theta$  sin  $\theta$ ') + i (sin  $\theta$   cos  $\theta$ ' + sin  $\theta$ ' cos  $\theta$ )].

Les adeptes de trigonométrie ont reconnu les formules d'addition connues :

z z' = r r' [cos ( $\theta$  +  $\theta$ ') + i sin ( $\theta$  +  $\theta$ ')].

Ainsi, non seulement le module d'un produit est le produit des modules, mais l'argument d'un produit est la somme des arguments. De là à créer des correspondances entre rotations ou similitudes du plan et multiplication des complexes, il n'y a qu'un pas, que vous franchirez dans le dossier suivant. 

Parmi les très nombreuses applications immédiates du dernier résultat, figure la célèbre « formule de Moivre » : 

(cos  $\theta$  + i sin  $\theta$ )ⁿ = (cos n  $\theta$  + i sin n  $\theta$ ).

À la lecture de ces quelques lignes, vous avez ainsi constaté comment les nombres complexes tracent des liaisons entre les différents domaines des mathématiques, liaisons qui seront développées dans les différents dossiers de ce numéro : algèbre, analyse et trigonométrie, géométrie.