Ces fous d'équations
qui créèrent les imaginaires

Les équations sont nées avec Diophante : le premier, il eut l'idée de nommer l'inconnue d'un problème. Il ne s'agit pas d'une idée banale car nommer est un moyen de dompter, de donner une réalité à ce que l'on nomme. Une fois nommée, l'inconnue devient passible de calculs. Diophante l'appelait arithmos, c'est-à-dire « le nombre » en grec. Chacun connaît ce terme, sur lequel le mot « arithmétique » a été forgé. Il écrivait ensuite les relations obtenues en toutes lettres. Cela donnait des phrases lourdes, même si elles restaient claires.

La tradition de Diophante passa aux mathématiciens arabes du Moyen Âge, qui changèrent le mot utilisé. Au IX^e siècle, al-Khwarizmi nommait l'inconnue shay, ce qui signifie « la chose ». Les algébristes italiens de la Renaissance utilisèrent le même mot, cosa en italien. Les Andalous, alors sous influence arabe, écrivaient ce mot en caractères latins, xay.

René Descartes accomplit l'ultime simplification en ne gardant que l'initiale de xay. La lettre x venait de trouver son emploi mathématique, et bientôt juridique, tout en gardant son sens de « chose [ou nombre, ou personne] que l'on cherche ».

Les algébristes de la Renaissance

 Le mot « algèbre » ne vient pas de l'utilisation d'une inconnue mais des manipulations de membres qu'utilisait al-Khwarizmi pour résoudre les équations. L'étymologie de ce mot est arabe. L'algébriste est celui qui manipule les membres des équations, ou des personnes. Ici, on utilisera les notations modernes pour montrer les manipulations que pratiquaient ces algébristes.

Les manipulations les plus simples concernent les équations du premier degré comme 2x + 1 = x + 5. Dans ce cas, l'algébriste fait passer le x du second membre dans le premier, ce qui donne x + 1 = 5, puis le 1 du premier membre dans le second, d'où le résultat x = 4. Pour résoudre l'équation du second degré x² + 6x = 7, l'algébriste remarque que x² + 6x est le début du carré (x + 3)². Il ajoute donc 9 aux deux membres pour obtenir (x + 3)² = 16 = 4². Longtemps, cette équation n'a donné qu'une seule solution, x + 3 = 4, donc x = 1. En effet, les solutions négatives étaient exclues. Nos algébristes évitaient toute quantité négative isolée, c'est-à-dire que « –4 » était interdit mais pas « x – 4 ». Notre équation x² + 6x = 7, qui n'avait autrefois qu'une solution (x = 1), en a acquis depuis une autre, négative, x = –7.

En dehors de la question des racines négatives, les mathématiciens grecs et arabes savaient résoudre les équations du second degré. Ils ont également rencontré des équations de degré 3, mais la résolution générale de ces équations est l'œuvre des algébristes italiens de la Renaissance. Le premier à avoir su résoudre un cas général, celui des équations sans termes du second degré, plus précisément celles de la forme x³ + px = q où p et q sont des entiers naturels, semble être Scipione Del Ferro. « Semble », car il n'a pas écrit sur le sujet, gardant ses découvertes dans un petit carnet, qu'il réservait à ses proches. Cette démarche était classique à l'époque où les défis algébriques étaient courants, et avaient des conséquences financières ou professionnelles. 

Les grandes heures des défis mathématiques

Del Ferro confia sa méthode à son gendre, Annibal de la Nave, qui fut trop bavard. C'est ainsi que la méthode passa à l'un de ses amis, Antonio Maria Del Fiore. Cependant, celui-ci garda le secret jusqu'à la mort de Del Ferro. Ensuite, il se mit à participer à des concours mathématiques qui, de ce temps, comportaient souvent des problèmes régis par des équations du troisième degré. Grâce au secret de Del Ferro, il savait les résoudre dans le cas sans termes du second degré.

Ces défis lancés aux mathématiciens italiens l'amenèrent à s'opposer à Niccolo Fontana, dit Tartaglia. Ce dernier devait son surnom de Tartaglia, « le bègue », à une blessure qu'il reçut lors du sac de Brescia par les troupes françaises en 1512. C'était un complet autodidacte, d'origine très modeste, qui vivait de cours de mathématiques et de concours, ce qui l'amena à trouver Del Fiore sur son chemin. Un duel algébrique eut lieu.

Chacun déposa chez un notaire trente problèmes, que l'autre devait résoudre dans les quarante jours. Ils correspondaient tous à des équations du troisième degré sous un habillage donnant l'illusion d'un problème concret. À titre d'exemple, voici l'un des problèmes de Del Fiore :

« Un usurier prête un capital à la condition qu'à la fin de l'année on lui paye pour intérêt la racine cubique du capital. À la fin de l'année, l'usurier reçoit 800 ducats, capital et intérêt. Quel est ce capital ? »

Si l'on note x l'intérêt en ducats, le capital est x³ et la condition du problème s'écrit x³ + x = 800.
Si le but était d'ordre pratique, il suffirait de remarquer que 10³ + 10 = 1 010 > 800 et 9³ + 9 = 738 < 800 pour affirmer que x vaut entre 9 et 10 ducats. Après quelques essais, on trouverait x = 9,24727, donc un capital de 790,75 ducats. Bien entendu, même si ce résultat suffit amplement pour régler les affaires d'un usurier et de son client, ce n'est pas la solution attendue ! Il s'agit de trouver une solution exacte exprimable avec des nombres entiers, les quatre opérations arithmétiques plus des radicaux. De fait, cette solution n'est guère exploitable dans une transaction commerciale, il s'agit de mathématiques pures. Voici la solution exacte telle qu'on peut la trouver après des calculs laborieux en appliquant la méthode de Tartaglia (voir plus loin) : 

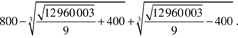
 Un peu de poésie… mathématique

Del Ferro ne savait résoudre qu'un seul type d'équations, celui mentionné précédemment ; ainsi, Tartaglia gagna mais renonça au prix. Il ne divulgua pas sa méthode avant l'apparition d'un autre personnage, Girolamo Cardano (1501–1576), appelé Jérôme Cardan en France, le père des cardans de nos voitures, qui était aussi médecin, mathématicien… et astrologue. Un personnage complexe ! En 1539, il fit venir Tartaglia à Milan, où il vivait, et réussit à le persuader de lui donner sa formule en promettant de ne pas révéler le secret. Tartaglia en avait fait un poème, dont voici le début dans une traduction française :

« Quand le cube auprès des choses

S'égale à quelque nombre discret,

Trouve en lui deux nombres différents.

Alors tu prendras pour habitude

Que leur produit soit toujours égal

Au tiers cubé des choses exactement. »

 

Le premier vers peut sembler énigmatique. Cependant, dans la filiation des mathématiciens arabes, « la chose » est l'inconnue, que nous nommons x, « les choses » en sont un multiple entier, c'est-à-dire px, et « le cube », x³.

Le deuxième vers introduit un nombre, soit q, et donc l'équation x³ + px = q. La suite expose la méthode… que publiera un peu plus tard Cardan dans son Ars magna. Tartaglia a été trompé… mais Cardan ne peut pourtant pas être pris pour un simple voleur car, non seulement il a su justifier les formules de Tartaglia, mais en outre il a traité tous les cas du troisième degré, et ajouté la résolution des équations du quatrième degré ! Son élève Ludovico Ferrari, au moyen de manipulations algébriques, avait en effet réussi à ramener la résolution de l'équation du quatrième degré à celle d'une équation du troisième.

Sans suivre tous les détails techniques, voyons comment Rafaele Bombelli mena la résolution de l'équation x³ = 15x + 4. Comme Tartaglia le recommande dans son poème (« trouve en lui deux nombres différents »), il posa d'abord x = u + v puis, suivant le conseil du mathématicien bègue, en imposant la contrainte supplémentaire uv = 5 (« leur produit égal au tiers cubé des choses »), il simplifia l'équation en u³ + v³ = 4. En posant U = u³ et V = v³, il arriva à un système classique depuis Diophante, où somme et produit de deux nombres (U et V ici) sont donnés (4 et 125). Il en déduisit que U et V étaient les solutions de l'équation du second degré X² – 4X + 125 = 0. Cette équation se transformait en (X – 2)² = –121.

Bombelli aurait dû arrêter son travail là, car cette équation n'a pas de solutions réelles ! Pourtant, il eut l'idée folle, et géniale, de continuer comme si –121 avait une racine carrée. Il la nota seulement  \( 11\sqrt{-1}\) et obtint donc U et V, puis u et v en fonction de ce nombre. Bombelli remarqua alors que x = u + v se simplifiait en x = 4. Le résultat est exact, comme on peut le vérifier a posteriori. Ainsi, un calcul a priori absurde sur des nombres impossibles, comme on les a d'abord nommés, permettait d'obtenir un résultat exact !

En fait, de nouveaux nombres étaient nés, sans que l'on comprenne bien ce qu'ils pouvaient signifier. Ils produisaient des résultats corrects, que l'on pouvait vérifier, et c'est pourquoi ils furent admis dans la grande famille des nombres. Descartes les nomma « imaginaires » pour les distinguer des autres qui, à cette occasion, devinrent les nombres « réels ». Ces nombres ne prirent une réalité que beaucoup plus tard sous le nom de nombres « complexes ».

Un concept était né de pures manipulations algébriques. Si l'on continue la résolution de l'équation de Bombelli, on obtient deux autres solutions,  \( x=-2+\sqrt{3}\) et  \( x=-2-\sqrt{3}\) . Ces solutions n'ont pas été trouvées par Bombelli. Ce n'était pas une erreur car il ne s'intéressait qu'aux solutions positives, même s'il ne craignait pas de passer par des nombres imaginaires pour cela !

La fameuse racine carrée de –1

La notation  \( \sqrt{-1}\) utilisée par Bombelli n'est plus guère admise en France dans l'enseignement secondaire, on lui préfère la notation i proposée par Euler au XVIII^e siècle (i étant l'initiale d'« imaginaire »). Le nom de « complexe » vient de Gauss, pour qui les mathématiques étaient ancrées dans la réalité physique et qui n'appréciait donc pas le terme d'« imaginaire » utilisé jusque-là.

En suivant la notation d'Euler, les nombres complexes sont de la forme a + i b où a et b sont des nombres réels. On parle de corps des nombres complexes pour désigner leur ensemble, car on peut y définir les quatre opérations et qu'elles y ont les propriétés habituelles (comme l'associativité, la commutativité et la distributivité). Comment procéder ? Il suffit d'ajouter, aux règles usuelles, la convention i² = -1.