HS Kiosque 61 : Les ensembles > Dossier : Nombres, opérations, structures

Construire des nombres, une histoire au long cours

Daniel Justens

dossier : Nombres, opérations, structures

HS Kiosque 61 : Les ensembles

Au commencement était le nombre... Si l'on remonte aux origines, ces objets étaient représentés par des cailloux avant d'être codés par des symboles. Des nombres, il y en a en fait pour tous les goûts ! C'est bien connu : quand on aime, on ne compte pas...

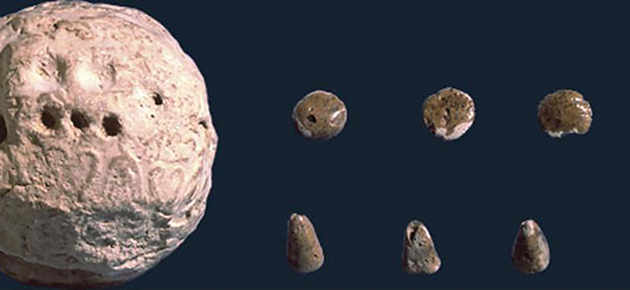
La construction progressive des ensembles de nombres a pris du temps. Au quatrième millénaire avant notre ère, pour enregistrer leurs opérations comptables, les Sumériens utilisaient un système de jetons modelés dans de l'argile, que l'on nomme calculi (du latin « petites pierres ») par analogie avec les cailloux qui servaient à l'apprentissage du calcul. Ceux-ci étaient glissés dans une sphère creuse, la bulle, sur laquelle était apposé un sceau. En cas de doute quant à la quantité de bêtes confiées à un berger, il suffisait de briser la bulle pour vérifier qu'aucune bête ne manquait. S'il n'y a pas nécessairement de correspondance entre les formes imprimées sur la bulle et celles des calculi qui y sont inclus, on observe toujours une correspondance de nombres. Vers –3300, on convint d'apposer sur la bulle, à côté du sceau, sous forme d'une sorte de bordereau, un résumé de son contenu, rendant ce dernier obsolète. Les bulles s'aplatirent pour devenir des tablettes. L'écriture et les premières représentations de nombres étaient nées de la nécessité du dénombrement. Mais quel chemin restait-il encore à parcourir pour arriver à la notion contemporaine de nombre !

La puissance de l'axiomatisation

Au commencement étaient les nombres entiers, dits naturels. Leur construction peut se faire, formellement, à partir de la théorie des ensembles, et plus particulièrement de l'ensemble vide. Le premier à en avoir proposé en 1889 une axiomatique satisfaisante est Giuseppe Peano (1858-1932). Comme toute axiomatique, elle est constituée d'hypothèses d'existence d'objets et de relations entre ces objets. Comme toute axiomatique, elle reprend nos schémas cérébraux constitués de neurones (objets) et de synapses (relations entre ces objets). Peano considère un ensemble $ \mathbb{N}$ contenant un élément particulier a et postule l'existence d'une application

$ S: \mathbb{N} \mapsto \mathbb{N}.$

Trois axiomes sont alors nécessaires et suffisants pour définir univoquement l'ensemble des naturels : on suppose que l'élément a ne possède pas d'image inverse par S ; que tout autre élément de $ \mathbb{N}$ possède une et une seule image inverse par S ; et enfin que si un sous-ensemble M de $ \mathbb{N}$ contient a et contient S(n) dès qu'il contient n, alors ce sous-ensemble coïncide avec $ \mathbb{N}$ .

Cet ensemble d'axiomes ne semble pas très intuitif. On devine néanmoins que l'élément particulier a va être notre 0 et que S(n) désignera le « successeur » de n. Le dernier axiome, appelé principe d'induction complète, garantit de pouvoir faire des raisonnements par récurrence. Le principe de récurrence est sans doute la propriété la plus fondamentale des entiers naturels, celle qui joue le rôle le plus important dans l'étude des fondements mathématique. Elle permet de définir rationnellement l'opération d'addition sur $ \mathbb{N}$ . On postule que pour tout n appartenant à $ \mathbb{N}$ , on a n + a = n. De plus, on pose, pour tous n et m appartenant à $ \mathbb{N}$ , n + S (m) = S (n + m). Pour définir une multiplication, il suffit de demander, pour tous n et m, que n × 0 = 0, et que n × S (m) = n × m + n. Ce qui est extraordinaire, c'est que l'ensemble des entiers naturels a pu être construit sans qu'il soit nécessaire de définir sémantiquement la notion de nombre ou de recourir à une quelconque représentation mentale intuitive de cette notion ! C'est là que réside la puissance de l'axiomatisation.

Toujours des trous…

Le recours aux deux opérateurs qui viennent d'être « définis » va engendrer des manques. En effet, l'addition dans les entiers naturels n'est pas réversible : si n est non nul, il n'existe pas d'autre entier naturel m tel que n + m = 0. L'ensemble des entiers relatifs va être introduit pour symétriser l'addition sur $ \mathbb{Z}$ . L'ensemble des entiers relatifs a une structure de groupe pour l'addition. Si l'on étend l'opérateur de multiplication à $ \mathbb{Z}$ , on en fait un anneau intègre (si un produit est nul, c'est obligatoirement qu'au moins un des facteurs est nul). Cette propriété permet parfois de résoudre des équations. Ce n'est pas nécessairement toujours le cas : dans l'anneau des matrices 2 × 2, muni de l'addition usuelle et de la multiplication matricielle, on a par exemple

$ \begin{pmatrix} -1 & 2 \\ 0 & 0 \end{pmatrix} \times \begin{pmatrix} 4 & 2 \\ 2 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \\ \end{pmatrix} $

Mais un nouveau problème se pose : l'absence de réversibilité de la multiplication ! Si n est un entier relatif distinct de 1, il n'existe pas d'autre entier m tel que n × m = 1. Il convient donc de compléter l'ensemble des entiers relatifs pour symétriser la multiplication : on construit alors l'ensemble Q des rapports n / m de deux entiers, le second étant non nul. Q fut baptisé ainsi par Peano en 1895 d'après l'initiale du mot italien quoziente, le quotient. On parle plus souvent de nombres rationnels, du latin ratio (un terme issu du radical ratus, participe de reor, qui signifie calculer). La boucle semble bouclée.

Des nombres de plus en plus complexes

Hélas, toutes les équations ne peuvent encore être résolues ! Ainsi la fonction définie par x² – 2 prend des valeurs positives et négatives sur Q, mais ne s'annule pas sur cet ensemble. On complète donc l'ensemble des rationnels. Ceci peut se faire au moyen des suites de Cauchy, ou (de manière équivalente) à l'aide des coupures de… Dedekind. C'est en 1858, alors qu'il enseignait à l'École polytechnique fédérale de Zurich, que le mathématicien allemand développe une nouvelle idée pour représenter l'ensemble complété des nombres rationnels par « division » de ce dernier. Pour lui, un nombre réel est une « coupure » qui sépare les nombres rationnels en deux ensembles, un ensemble supérieur et un ensemble inférieur. Pour reprendre l'exemple de x² – 2, le nombre « racine carrée de 2 » sera la coupure entre l'ensemble comprenant tous les nombres négatifs et les positifs ayant un carré inférieur à 2 et l'ensemble des nombres positifs ayant un carré supérieur à 2. Les réflexions de Dedekind sur la définition rigoureuse des nombres irrationnels par les coupures sont l'objet du mémoire Stetigkeit und irrationale Zahlen (continuité et nombres irrationnels) publié en 1872.

Enfin, même cet ensemble des réels n'est pas encore totalement satisfaisant, car il existe des équations polynomiales, comme x² + 1 = 0, qui n'y ont pas de solutions. Il faut donc introduire l'ensemble des nombres complexes. Mais ceci est une autre histoire…

références

Les matrices. Bibliothèque Tangente 44, 2012.
Bien commencer ses études supérieures en mathématiques. Henri Lemberg, Vuibert, 1997.

Accéder à l'ensemble du numéro

Revenir au sommaire du numéro

-- -- -- -- -- -- FOCUS -- -- -- -- -- --

L'éclectique Giuseppe Peano

L'éclectique Giuseppe Peano

Quel parcours que celui du mathématicien et linguiste italien Giuseppe Peano ! Il utilise les symboles formels de la théorie des ensembles pour donner une présentation unifiée des mathématiques et introduit nos notations actuelles pour désigner réunion et intersection. Dès 1889, il propose une définition axiomatique de la notion d'espace vectoriel et de l'ensemble des entiers naturels.

Son nom reste également rattaché à la courbe de Peano, découverte en 1890. Les travaux de Cantor avaient conduit à considérer différents type d'infinis, dont les deux plus « simples » sont le dénombrable et le continu. On peut présenter des ensembles dénombrables, qui ont « autant d'éléments » qu'il y a d'entiers dans $\mathbb{N}$ , et des ensembles continus, qui ont « autant d'éléments » que $\mathbb{R}$ . Or, il y a autant d'éléments dans le segment [0, 1] que dans [0, 2], ou même dans $\mathbb{R}$ lui-même. Mais notre génial Italien est allé plus loin : il a créé une courbe, paramétrée par une fonction continue sur [0, 1] et surjective sur le carré [0, 1] × [0, 1]. Intuitivement, il a montré (ce qui avait été prouvé par Cantor en 1877) qu'il y avait autant d'éléments dans le côté d'un carré que dans le carré lui-même !

Peano fut également l'inventeur d'une langue universelle, le latin sans flexion. Hélas, le mieux étant l'ennemi du bien, l'abus progressif de symboles dérouta les étudiants de Peano, qui fut renvoyé de l'Académie royale militaire.

Les origines italiennes des complexes

Les origines italiennes des complexes

Un des premiers mathématiciens à avoir osé imaginer les nombres complexes est italien, c'est Girolamo Cardano, qui a par la suite francisé son nom en Jérôme Cardan. En 1545, dans son Artis magnae sive regulis algebraicus, il propose comme solutions à l'équation x (10 – x) = 40 des nombres à la forme bizarre qu'il écrit 5.p.R.m15 et 5.m.R.m.15. Il avait osé ! Sa solution, que nous lisons aujourd'hui $5+\sqrt{-15}$ et $5-\sqrt{-15}$ , était transgressive pour l'époque, même s'il prenait le soin de préciser que le produit de ces deux nombres, qu'il appelait des « quantités sophistiques » (souvent traduit par « quantités sophistiquées », qui est un faux sens), était bien égal à 40.

Un autre mathématicien italien, Rafaele Bombelli, imagine en 1572 quelles pourraient être les règles de calcul sur de tels nombres : il y avait déjà les signes + (piu) et – (meno), auxquels il va en ajouter deux autres, qui permettront d'ajouter ou retrancher des racines de nombres négatifs : piu di meno et meno di meno. Cela lui fera écrire 5 piu di meno R.q. 15 ce qu'aujourd'hui nous écririons $5+i \sqrt{15}$ , selon la notation donnée par la suite par Descartes, avec « i » comme « imaginaire », évitant par la même occasion la notation $\sqrt{-15}$ . Il codifiera les opérations avec ces signes d'un nouveau genre : piu di meno via meno fà meno di meno, que nous lirions aujourd'hui « + i par – donne – i ». É.B.

Le latino sine flexione

Le latino sine flexione

Le latin fut longtemps LA langue de la science. Newton publia ses Philosophiae Naturalis Principia Mathematica en latin (en 1687). Au cours du XVIII^e siècle, le français prit le relais. Mais dès le XIX^e siècle, le nombre de chercheurs s'amplifie et chacun publie dans sa langue natale ; la situation devient inextricable. C'est l'époque de la création de langues artificielles, comme le volapük (inventé vers 1880 par le prêtre allemand Johann Martin Schleyer sur « commande de Dieu lui-même », Schleyer regrettait sans doute la « babélisation ») ou l'espéranto, du Polonais Ludwik Zamenhof, le « docteur qui espère ». En 1903, alors que le recours à une langue vivante comme langue universelle paraît à tous utopique, Giuseppe Peano propose un retour au latin simplifié, sans conjugaison et sans déclinaison, la place des mots dans la phrase indiquant leur fonction : l'interlingua. Ses simplifications, remettant en cause certaines parties du discours, comme le verbe ou le substantif, ne sont pas arbitraires : elles s'appuient sur les travaux logiques de Leibniz, et ceux du linguiste français Michel Bréal. C'est dans cette langue qu'il entreprend la rédaction du Formulario mathematico, une véritable encyclopédie des mathématiques… Ce qui explique sans doute son peu de succès…

À l'aube de la Première Guerre mondiale, trois langues dominent la scène internationale : l'anglais (du fait de son empire colonial), le français (langue de la diplomatie) et l'allemand (langue scientifique importante). Après la guerre, l'Allemagne défaite et la France exsangue ne peuvent plus entrer en compétition avec l'anglais, qui devient la langue des échanges internationaux et donc de la science.

Les axiomes de Peano

Les axiomes de Peano

1. L'élément appelé zéro et noté 0 est un entier naturel.

2. Tout entier naturel n a un unique successeur, noté s (n).

3. Aucun entier naturel n'a 0 pour successeur.

4. Deux entiers naturels ayant le même successeur sont égaux.

5. Si un ensemble d'entiers naturels contient 0 et contient le suc- cesseur de chacun de ses éléments, alors cet ensemble est égal à XXXXXXX. Le premier axiome ne dit rien d'autre que « l'ensemble des natu- rels n'est pas vide », le troisième qu'il possède un premier élément et le cinquième introduit le principe de récurrence. C'est à Peano que l'on doit également la notation N en caractère gras pour les nombres entiers positifs et N₀ pour les entiers positifs ou nuls. La notation évoluera ensuite vers notre XXXXXXX moderne.