Apparue dans le cadre de la résolution d'équations au XIXe siècle, et vite devenue inévitable, la notion de groupe a permis de mettre en exergue des analogies entre des situations a priori bien différentes. Essayons de comprendre pourquoi les mathématiciens ont l'esprit de groupe.

Vous pouvez les réorganiser autrement, par exemple en agissant ainsi : 

Une première permutation, 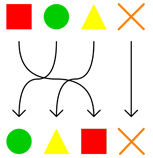\( \sigma_1\)  : 

 

Ce réarrangement est une permutation des quatre objets.

Il existe bien d'autres permutations ; en voici une deuxième.  

Une deuxième permutation, 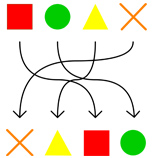 \( \sigma_2\)  : 

 

Quand les structures sont les mêmes… 

Voilà un jeu bien amusant ; quelle structure se cache derrière tout ça ?

Ce qui peut paraître surprenant au premier abord, c'est le fait de considérer que l'ensemble des
permutations de quatre objets n'est pas sans rappeler l'ensemble des entiers relatifs. Pour s'en rendre compte, il ne faut pas seulement s'intéresser à ces deux ensembles comme de simples collections d'objets, mais les munir aussi d'une opération. Pour les entiers, ce sera l'addition. On peut toujours additionner deux entiers : le résultat de cette opération produit encore un entier.

Pour les permutations, ce sera la composition : il suffit de les enchaîner l'une après l'autre pour obtenir encore une permutation. Voici ce que donnerait par exemple l'enchaînement des deux permutations  \( \sigma_1\)  et \( \sigma_2\) . On note cette nouvelle permutation  \( \sigma_2\circ\sigma_1\) .

Composition de deux permutations :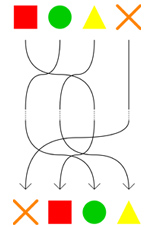  

 

Les parenthèses sont inutiles dans les deux cas : si a, b et c sont trois entiers, alors (a + b) + c = a + (b + c) ; de même, si \( \sigma_1\) _{, \( \sigma_2\)}  et \( \sigma_3\)   sont trois permutations, alors

  \( (\sigma_1\circ\sigma_2)\circ\sigma_3 = \sigma_1\circ\(\sigma_2\circ\sigma_3)\) .

Dans les deux cas, un élément ne change rien : l'élément neutre. Pour les entiers et l'addition, c'est le nombre 0. En effet, a + 0 = 0 + a = a. Voyez-vous quel élément joue ce rôle pour les permutations ? Il s'agit tout simplement de la permutation qui consiste à… ne changer aucun élément de place !

Pour finir, chaque élément possède un symétrique (un inverse par rapport à l'élément neutre). Pour les entiers, il suffit de considérer leur opposé : a + (–a) = –a + a = 0. Pour les permutations, il suffit de remettre les éléments à leur place en suivant les flèches des diagrammes dans l'autre sens.

La permutation inverse de 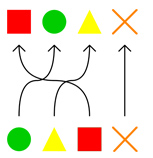\( \sigma_1\)  :  

 

Les deux exemples évoqués pour le moment semblent bien différents. Il existe par exemple une infinité de nombres entiers alors qu'ils n'y a que vingt-quatre permutations de quatre éléments. Pourtant, certains caractères communs apparaissent, qui permettent de définir un groupe.

Un groupe est donc un ensemble G muni d'une opération, que l'on peut noter *. Quatre conditions doivent être vérifiées :

• Le résultat de l'opération est encore un élément de G (* est une loi de composition interne). Le produit scalaire ne peut donc pas être retenu comme exemple de telle loi : il associe un nombre réel à deux vecteurs ;

• La loi est associative, c'est-à-dire que l'on a toujours (a * b) * c = a * (b * c). Certaines opérations ne vérifient pas cette relation ! C'est par exemple le cas de l'exponentiation : (2²)³ = 4³ = 64 alors que 2⁽²³⁾ = 2⁸ = 256 ;

• Il existe dans G un élément neutre e, c'est-à-dire un élément qui vérifie a * e = e * a = a pour tout élément a de G ; 

• Pour chaque élément a de G, il existe un élément de G, souvent noté a^–1, tel que a * a^-1 = a^-1 * a = e.

Voyez-vous d'autres exemples de groupes ?

 

L'ensemble des permutations de n éléments muni de la composition en est un, on le note souvent \( \mathcal{S}_n\) . L'ensemble des nombres réels non nuls muni de la multiplication en est un autre.

Ces quatre conditions peuvent sembler bien élémentaires. Elles sont pourtant d'une richesse extraordinaire ; plusieurs décennies ont été nécessaires pour bien les identifier. Les groupes se sont par la suite révélés utiles dans l'étude des équations différentielles, en physique fondamentale, en chimie et même en ethnologie dans les travaux de Claude Lévi-Strauss (voir Tangente 135, 2010). Henri Poincaré affirma en son temps que « toutes les mathématiques sont une histoire de groupes ». Quelques années plus tard, l'immense Alexandre Grothendieck n'hésitera pas à proposer l'invention du zéro et l'idée de groupe comme les deux plus grandes innovations mathématiques de tous les temps !

  
En géométrie, partout

 

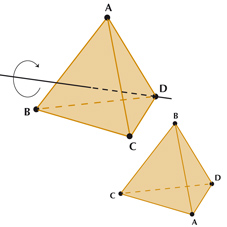 Les groupes sont en effet omniprésents. Un objet emblématique de la géométrie est le tétraèdre régulier. Certaines transformations de l'espace laissent un tel polyèdre invariant. C'est le cas de la rotation d'angle 120° et d'axe la hauteur de ABCD passant par D.

Si vous êtes observateur, peut-être aurez-vous remarqué que cette transformation n'est pas sans rappeler la permutation \( \sigma_1\)  présentée au début de cet article. Il suffit de renommer respectivement le carré, le disque, le triangle et la croix par les sommets A, B, C et D. La permutation consistant à échanger seulement deux éléments correspond dans le cas du tétraèdre à une symétrie par rapport au plan médiateur d'une arête.

Parviendrez-vous à identifier la transformation géométrique qui se cache derrière la permutation  \( \sigma_2\)  ? Petit indice : il faut enchaîner une rotation et une symétrie.

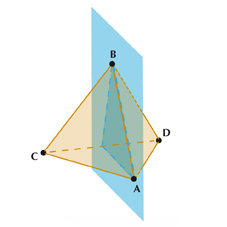En fait, le groupe des permutations \( \mathcal{S}_4\)  est le même que le groupe des isométries qui conservent le tétraèdre régulier. On voit là tout l'intérêt d'analyser la structure de groupe d'un ensemble.

Attention cependant, tous les groupes qui stabilisent un objet géométrique ne sont pas des groupes de permutations ! Regardons par exemple le cas du carré : aucune isométrie du plan ne permet d'échanger seulement deux sommets adjacents…

 

 

 

 

De la même façon que l'on peut considérer les différentes parties d'un ensemble, on peut considérer les différentes parties d'un groupe. Certaines s'avèrent particulièrement intéressantes car elles conservent elles aussi une structure de groupe : ce sont les sous-groupes. Reprenons l'exemple des isométries conservant un carré.

 

 

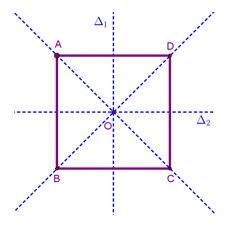
En tout, huit transformations appartiennent à ce groupe, souvent noté D₈. On y trouve l'identité, évidemment, les rotations de centre O et d'angle 90°, 180° et 270°, ainsi que les symétries d'axe (AC), (BD), \( \Delta\) ₁ et \( \Delta\) ₂. On peut résumer les relations entre ces différents éléments dans une table :

 

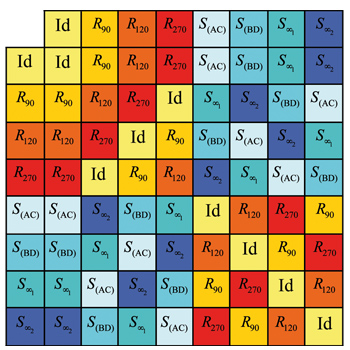
^{La table de D₈.}

 

Le jeu des couleurs permet de constater rapidement que l'ensemble constitué de l'identité et des trois rotations forme à lui tout seul un groupe. Ce sous-groupe de D₈ est le groupe cyclique d'ordre 4, noté \( \mathbb{Z}/4\mathbb{Z}\) .
Les groupes cycliques d'ordre n sont engendrés par un seul élément. Ils correspondent à l'addition modulo n. Par exemple, modulo 4, on a 1 + 3 = 0 et 3 + 2 = 1.

 

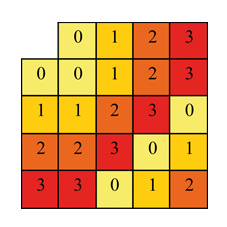
 La table de   _{\( \mathbb{Z}/4\mathbb{Z}\)}  .

La table de  \( \mathbb{Z}/4\mathbb{Z}\) est symétrique : l'ordre dans lequel on effectue l'opération n'a aucune influence sur le résultat. On dit que le groupe est commutatif, ou abélien. Ce n'était pas le cas du groupe D₈ car l'enchaînement des symétries S_(BD) et \( S_{\Delta_t}\) ne correspond pas à une même rotation.

 
Des recherches passionnantes

L'existence des groupes cycliques permet d'affirmer qu'il existe des groupes finis de n'importe quel ordre. Par ailleurs, Cayley a démontré en 1878 que tout groupe fini est un sous-groupe d'un groupe de permutations. Les amateurs de casse-tête se seront rendu compte que les jeux de type taquin ou cube de Rubik ne se résument finalement qu'à l'étude d'un certain sous-groupe de permutations !

 

La description des groupes finis a été l'objet d'une longue épopée qui n'a pris fin que dans les années 1980. Cet énorme travail a été le fruit des recherches d'une bonne centaine de mathématiciens à travers le monde et a débouché sur la publication par l'Oxford University Press d'un atlas des groupes finis (par John Conway, Robert Curtis, Simon Norton, Richard Parker et Robert Wilson). 

L'aventure des groupes ne s'arrête cependant pas là : les recherches sur le sujet sont encore nombreuses et passionnantes !