La notion d'ensemble, qui nous est si familière, n'a jamais fait surface en mathématiques avant les travaux du mathématicien allemand Georg Cantor. On parlait alors de « variété », de « totalité », de « classe » et Cantor a inventé non seulement un tout autre langage, mais l'axiomatique qui va avec, ouvrant la boîte de Pandore d'une théorie alors incongrue, dont il n'avait sans doute pas prévu tous les développements ni tous les excès.

Cantor : nommer les concepts

Avant le milieu du XIX^e siècle, en mathématiques, les concepts primaient sur la rigueur des énoncés. On avait bien rencontré chez Augustin Cauchy (1789–1857) et chez Bernard Bolzano (1781–1848) des esquisses de clarification de notions comme la continuité, la limite, la convergence en analyse, mais c'est avec les Allemands Georg Cantor et Richard Dedekind (1831–1916) que les objets mathématiques prennent réellement un nom. En 1883 paraît dans les Acta Mathematica une version française des mémoires publiés par Cantor depuis 1870, première ébauche de sa Mengenlehre, devenue notre « théorie des ensembles ». Très préoccupé par les problèmes de dénombrement, plus particulièrement celui de « compter » l'infini, Cantor se pose en ces termes le problème de l'identification de deux fonctions f et g représentées toutes deux par des séries trigonométriques, mises au point par Joseph Fourier quelque cinquante ans plus tôt : que se passe-t-il si f(x) = g(x) partout sauf sur un ensemble « exceptionnel » ? C'est alors que Cantor jette, en une centaine de pages, les bases de « sa » théorie des ensembles.

À lui d'avoir défini un ensemble comme une « réunion M d'objets de notre conception, déterminés et bien distincts, que nous nommerons éléments de M », utilisant déjà les majuscules pour nommer les ensembles et les minuscules leurs éléments. À lui aussi d'avoir codifié, dans les six mémoires qu'il publie entre 1878 et 1884, des termes comme équipotence, cardinal, puissance d'un ensemble, ensembles emboîtés ou ensemble bien ordonné (qui donnera par la suite le théorème du bon ordre). À lui encore d'avoir défini les ensembles dérivés (ensemble des points d'accumulation d'un ensemble) et d'avoir, chemin faisant, créé des ensembles que l'on pouvait dériver une infinité de fois, développant une véritable « arithmétique de l'infini ».

L'approche de Cantor, qui, à partir de ses découvertes sur l'infini, élabore sa théorie au départ « naïve », en plus d'offrir une base aux mathématiques (du jamais vu depuis Euclide !), est radicalement novatrice. Elle parle surtout d'ensembles infinis et voilà qu'elle les définit, de manière complètement iconoclaste pour l'époque, comme susceptibles de permettre une bijection entre eux et une de leur parties strictes ! L'étonnement est tel que Cantor lui-même, ayant établi que les ensembles R et R² étaient équipotents, écrit à son ami Dedekind, qui l'a toujours soutenu dans ses initiatives et a su prolonger ses travaux : « Je le vois, je ne le crois pas ! »

Avant, après 

À la théorie des ensembles existe un « avant » et un « après ». Les mathématiciens s'en sont assez vite emparés, soit pour la critiquer, soit pour l'enrichir.

Dans ses textes, Cantor essaie de convaincre avec force détails, comme lorsqu'il tente de mettre en correspondance deux grandeurs variables a et b « de telle nature qu'on puisse les joindre l'une à l'autre de façon complète et à sens unique ». Joignant le geste à la parole, il accompagne ses propos par un dessin devant montrer que « le champ de l'une et l'autre [des grandeurs] a la même puissance ».

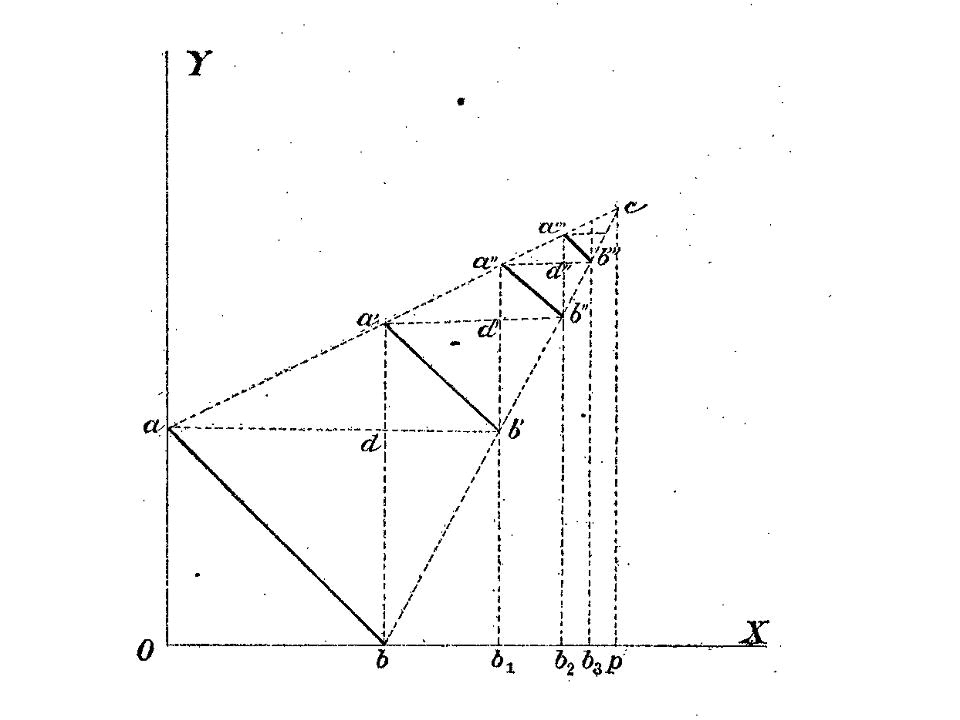^{Cantor, un essai de rigueur, mais des démonstrations encore naïves.}

Il peine cependant à obtenir l'assentiment de certains de ses contemporains, comme Hermann Schwarz et surtout son ancien professeur Léopold Kronecker, qui estimait que l'œuvre de Cantor manquait de rigueur. Kronecker, qui souhaitait fonder sur l'intuition des entiers toutes les mathématiques, déclarant que « Dieu a fait les nombres entiers, tout le reste est l'œuvre de l'homme », l'a même parfois violemment attaquée publiquement. D'autres de ses collègues détectent très vite les failles de la théorie émise par Cantor et mettent en avant les paradoxes qu'elle soulève. Le plus connu d'entre eux est le paradoxe de Russell : l'ensemble de tous les ensembles n'appartenant pas à eux-mêmes appartient-il à lui-même ? Cette question sera popularisée sous la forme du « paradoxe du barbier » : le barbier du village rase tous les hommes qui ne se rasent pas eux-mêmes. Le barbier se rase-t-il lui-même ? Si c'est oui, il rase quelqu'un qui se rase lui-même (le barbier), si c'est non, il y a une personne qui ne se rase pas elle-même (le barbier) et qui n'est pas rasée par le barbier : dans les deux cas, nous sommes en pleine contradiction.

Quelques modifications à la théorie des ensembles vont donc s'imposer, et Cantor lui-même va en proposer une partie dans sa correspondance avec Dedekind et ses collègues de Göttingen David Hilbert et Ernst Zermelo. Ce dernier fait d'ailleurs émerger l'idée qu'il est temps de passer à la phase d'axiomatisation et propose en 1908 un premier système d'axiomes pour la théorie des ensembles : le premier dit à quelle conditions deux ensembles sont égaux (extensionalité), le deuxième permet de construire des ensembles à partir d'une propriété donnée (compréhension), le troisième est un axiome d'existence, le quatrième définit la réunion de deux ensembles, le cinquième l'ensemble des parties d'un ensemble, le sixième le produit cartésien de deux ensembles, et on y ajoute encore l'axiome du choix (à partir d'une famille d'ensembles non vides, on peut construire un nouvel ensemble qui contient un élément de chaque ensemble de cette famille). Ce système d'axiomes est complété en 1920 par Abraham Fraenkel pour donner le célèbre système d'axiomes ZFC (« Zermelo-Fraenkel avec axiome du choix »), puis enrichi par John von Neumann.

Dit comme cela, tout paraît idyllique ; c'est sans compter les controverses déclenchées à chaque ajout, à chaque nouvelle publication. Il est même de ces publications qui, dès le début, ont failli ne pas voir le jour : par exemple quand, en 1883, le mathématicien français Charles Hermite exprime « l'impression désolante que nous produisent les mémoires de Cantor » et tente d'en couper certaines parties au moment de leur publication dans la revue Acta Mathematica. Certains mathématiciens, comme Émile Borel, ayant utilisé dès le début les notions de la théorie des ensembles, sont par la suite saisis par le doute et émettent des réserves sur ses points les plus généraux. D'autres, au contraire, le Suédois Mittag-Leffler en particulier, ont diffusé les idées de Cantor en France et en Allemagne.

L'hypothèse du continu 

Les notions apportées par cette théorie vont faire tache d'huile à travers toute l'Europe : Jacques Hadamard suggère en 1897 de l'utiliser pour étudier les ensembles de fonctions, René Baire fait en 1898 une thèse où interviennent des fonctions discontinues limites de fonctions continues, utilisant les nombres transfinis de Cantor. Certains nuages vont subsister : nouvelles attaques, mais aussi nouvelles avancées, jusqu'aux travaux de Kurt Gödel montrant en 1938 que les axiomes ZFC ne prouvaient pas la négation de l'hypothèse du continu, émise par Cantor, selon laquelle il n'existe aucun ensemble de cardinal strictement compris entre celui de l'ensemble des entiers naturels et celui de l'ensemble des réels. Hilbert en a d'ailleurs fait le premier de sa célèbre liste de vingt-trois problèmes proposée aux mathématiciens réunis au congrès de 1900. D'autres par la suite ont repris le flambeau, John von Neumann allant jusqu'à  proposer entre 1925 et 1930 une reformulation des axiomes ZFC en une nouvelle « théorie des classes ». Le mathématicien américain Paul Cohen prouvera même en 1963 l'indécidabilité de la fameuse hypothèse du continu dans le système ZFC. N'oublions pas non plus que le premier tome des Éléments de mathématiques du « mathématicien polycéphale » Nicolas Bourbaki est consacré à la théorie des ensembles. C'est à ce groupe de mathématiciens, persuadés que « la mathématique est destinée à survivre » que l'on doit une bonne partie du vocabulaire et des notations encore utilisés aujourd'hui, plus d'un siècle après Cantor, prouvant ainsi, comme le disait avec tant de prescience Hilbert, que « personne ne pourra plus nous chasser du paradis que Cantor a créé ».