Jeu, Set et maths

Set est un jeu de société crée par Marsha Falco, très populaire en Grande-Bretagne et édité en France par Gigamic. Il est constitué de quatre-vingt-une cartes, toutes différentes. Chacune présente des symboles qui combinent trois formes (losange, ovale et vague), trois couleurs (rouge, violet et vert), trois nombres (1, 2 et 3) et trois types de remplissage (hachuré, plein et vide). Le jeu peut être joué par deux à huit personnes.

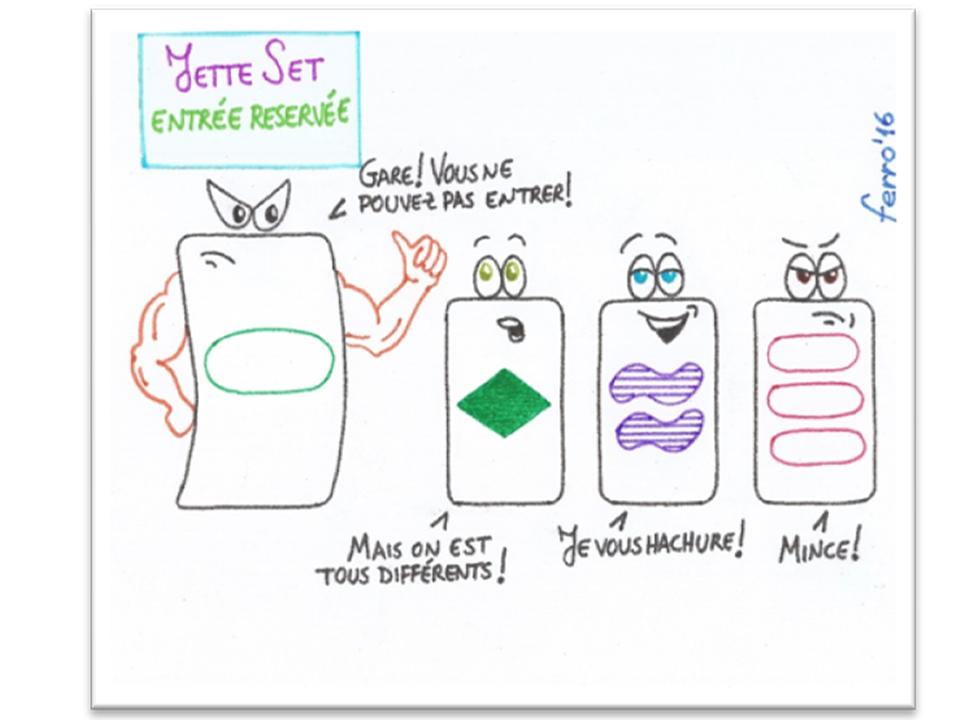
On dispose douze cartes en un rectangle 3 × 4 sur une table. Le but du jeu est de trouver le maximum de sets possible. Un set est composé par trois cartes qui doivent respecter les critères suivants : les formes sont toutes trois identiques ou totalement différentes ; les couleurs sont toutes trois identiques ou totalement différentes ; les nombres sont tous trois identiques ou totalement différents ; les remplissages sont tous trois identiques ou totalement différents. Par exemple, ci-dessous, le gardien du club a tort de ne pas permettre aux trois cartes d'entrer, une fois qu'elles sont toutes totalement différentes…

Dès qu'un joueur observe un set, il doit l'annoncer et montrer aux autres joueurs les trois cartes pour que ceux-ci vérifient. Alors, les trois cartes sortent de la table et sont remplacées par trois autres cartes de la pile. Si dans l'ensemble de douze cartes il n'y a pas un set, on ajoute trois cartes. Si, malgré cela, il n'y a pas de sets, on ajoute encore trois cartes de plus. Quand il n'y a plus de cartes dans la pile et il n'y a plus de sets dans la table, la partie est finie.
 

Le jeu de Dobble

Dobble est un jeu de société crée par la société Play Factory et édité en France par Asmodee, où l'observation et la rapidité sont au menu. Le jeu est composé de cinquante-cinq cartes en forme de cercle où s'affichent huit symboles différents les uns des autres.

La particularité ensembliste des cartes de Dobble est que, si l'on compare deux cartes quelconques, il y a toujours un et un seul symbole en commun. Cette fascinante contrainte est la base du jeu, consistant à repérer ce symbole avant les autres joueurs (cinq règles de mini-jeux à pratiquer entre deux et huit joueurs sont fournies avec les cartes).

Mais comment est-il possible de construire un tel jeu ? La réponse combinatoire à cette question sera donnée dans la version bibliothèque du présent hors-série… Pour l'heure, le lecteur est invité à réfléchir à un problème plus limité, qui le mettra sans doute sur la voie. On suppose que les cartes respectent la contrainte du Dobble, mais en contenant chacune trois symboles différents. On ajoute une autre contrainte : tous les symboles doivent partager le même nombre de cartes (par exemple, il ne peut pas y avoir le même symbole en commun sur toutes les cartes).

Combien le jeu contient-il de cartes ? Et combien de symboles différents sont employés en tout ? Une indication : il y a deux possibilités (la solution est sur le site tangente-mag.com). Curieusement, en généralisant à huit symboles par carte, la réponse n'est pas 55…

Set : un problème résolu !

Combien de cartes, au maximum, peut-on poser sur la table en jouant au Set sans qu'aucun des adversaires n'ait la possibilité de jouer ? Pour notre jeu initial de quatre-vingt-une cartes, la réponse, C₄ = 20 cartes, peut s'obtenir en dénombrant toutes les possibilités. De manière équivalente, combien de cartes doit-on considérer pour garantir l'existence d'un set ? C'est évidemment un de plus que le nombre C₄ précédent.

Ces questions, anodines en apparence, conduisent en fait à un redoutable problème de combinatoire, le cap set problem (problème de l'ensemble plafonnant). Considérons en effet n ≥ 4 symboles, au lieu des quatre dans le jeu de Set. Comment évolue le nombre C_n en fonction de n ?

 Des dénombrements parfois fastidieux permettent de se convaincre que C₂ = 4, C₃ = 9, C₄ = 20 (c'est le cas de Set), C₅ = 45. Les valeurs suivantes sont difficiles à obtenir. On conjecturait que, asymptotiquement, C_n ≤ cⁿ avec c < 3 une constante. Ces derniers mois, justement, une telle estimation a été obtenue : pour n « grand », Jordan Ellenberg et Dion Gijswijt ont réussi à majorer C_n par 2,756ⁿ, générant ainsi depuis quelques semaines de spectaculaires retombées en combinatoire.