Son grand œuvre : la logique

Lewis Carroll était en fait simple répétiteur et ses « travaux pratiques » n'ont jamais rencontré de succès, sans doute à cause du ton sec et magistral qui était le sien. Il décida d'interrompre son enseignement définitivement à l'âge de 49 ans alors qu'il n'attirait plus qu'une demi-douzaine de spectateurs (plutôt que de participants).

Lewis Carroll fut un logicien passionné. Dans les dernières années de sa vie, après avoir renoncé à la photographie, il abandonna tout ouvrage burlesque ou fantastique pour ne se consacrer qu'à la logique. Il accumula les matériaux qui lui serviraient, pensait-il, à composer son grand œuvre en la matière. Sa mort ne lui permit pas de mener cette tâche à bonne fin.

Il essaya de rédiger des règles de logiques et de syllogistiques, afin de vulgariser, particulièrement auprès des enfants, ces règles qui avaient disparu des programmes scolaires.
 

L'apparition des diagrammes 

Après une petite plaquette d'un jeu, publiée sans grand succès en 1886, The Logical Games, Carroll fait paraître en 1895 un ouvrage qu'il présente comme le tome I d'un « jeu intellectuel passionnant pour enfants et jeunes ». Le livre, qui fourmille d'exercices, s'apparente plus à un manuel qu'à un jeu. Si ses brochures de logique ou de mathématiques ont été publiées (et boudées) sous son vrai nom, Symbolic Logic est publié sous son pseudonyme. Le nom choisi et la qualité du livre entraînent un succès incontesté (trois rééditions jusqu'en 1897). Il faut attendre ensuite 1955 pour que soit repris en un volume Symbolic Logic And The Logical Games (Dover). La traduction de Symbolic Logic, Logique sans peine, est publiée en 1966 chez Hermann, présentée par Jean Gattégno et délicieusement illustrée par Max Ernst. Elle comporte une belle analyse de la méthode des diagrammes montrant les mérites comparés de Venn et de Carroll, sur les traces de Boole, créateur de la logique moderne.
 

Vers des représentations visuelles modernes

Contrairement à son contemporain John Venn, Carroll refusait la différenciation posée a priori entre l'attribut et sa négation. Ainsi, pour lui, les attributs « barbu » et « imberbe » ont la même valeur, et il ne trouve pas opportun que l'un soit représenté par un espace clos et l'autre par un espace non clos (voir l'article sur les diagrammes de Venn dans le premier dossier). Il propose donc une représentation dans laquelle l'« univers » est un carré, et chaque attribut divise ce carré en deux parties égales. Deux attributs x' et y' divisent l'univers en quatre, trois attributs en huit… Carroll transcrira attributs et univers successivement selon des diagrammes de plus en plus simplifiés et parlants.    

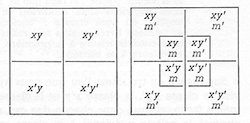
^{Représentation de deux attributs (à gauche) et de trois attributs (à droite).}

_{« Ancien » est l'attribut x, « anglais » l'attribut y, par opposition à « nouveau » (attribut x' ) et à « étranger » (attribut y' ).}

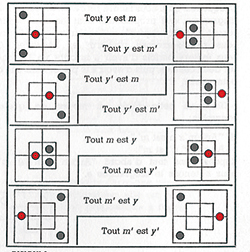
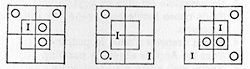
Dans un diagramme avec jetons, les cellules vides (« aucun xy n'existe », soit « aucun x n'est y » et « aucun y n'est x ») sont munies de jetons gris, celles ayant un contenu (« quelques xy existent », soit « quelques x sont y » et « quelques y sont x » sont munies de jeton rouges. Carroll remplace ensuite les jetons gris et rouges respectivement par O (« il ne se trouve rien ici ») et I (« il y a quelque chose ici »).