Le théorème des accroissements finis permet de garantir que des problèmes très concrets de capitalisation possèdent bel et bien une solution, et que l'on aboutit bien à cette solution en suivant les équations d'évolution standard. Un rêve pour tout économiste !
Les problèmes réels se traduisent très rarement par des équations admettant des solutions dont on peut proposer une forme algébrique simple et calculable directement. Le recours à des méthodes de calcul approché est le plus souvent indispensable. Assez curieusement, le théorème de Rolle ou son principal corollaire, le théorème des accroissements finis, permettent la mise en place de méthodes d'approximations successives convergeant vers la solution de certains problèmes réels tout en donnant une bonne idée du niveau d'erreur entachant la solution approchée.
Exploiter les relations de récurrence
Plaçons-nous dans la situation où il faut résoudre, numériquement, une équation du type f(x) = 0, et imaginons qu'il soit possible de la transformer en une équation équivalente du type )
. En partant d'une valeur arbitraire initiale x0, on peut construire une suite de valeurs (xk) en utilisant la relation de récurrence )
. Lorsque la suite ainsi construite converge, elle converge forcément vers la solution de l'équation initiale f(x) = 0. Une condition suffisante de convergence découle de Rolle. En effet, la suite de valeurs va converger si la limite (pour k tendant vers l'infini) des différences successives |xk – xk–1| tend uniformément vers 0. Or, le théorème des accroissements finis nous permet d'affirmer qu'il existe un point 
compris entre xk–1 et xk tel que
On en tire :
À chaque itération, l'écart entre deux valeurs successives est multiplié par une valeur particulière de la dérivée de la fonction 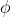. Si l'on peut trouver un majorant inférieur à un nombre strictement inférieur à 1 pour cette dérivée, la convergence est assurée ! Reste évidemment à quantifier la vitesse de cette convergence, ce qui peut se faire dès que l'on connaît le majorant. Voilà une méthode efficace et simple à programmer, qui va se révéler utile pour toute une gamme d'applications.
Des exemples d'utilisation de telles procédures se trouvent en finance, avec des efficacités diverses. Étudions le cas d'un placement sur compte bancaire à une date quelconque avec retrait à une autre date quelconque, en sachant que l'organisme financier nuance ses intérêts en les agrémentant de primes ou en les tempérant de frais, tout en capitalisant systématiquement le 1er janvier de chaque année. Les capitalisations successives à intérêt simple livrent une équation théorique d'évolution du type C(t) = C0(1 + d1i)(1 + i)n(1 + d2i).
Une première capitalisation a lieu après une première durée décimale d1 (écart entre la date de dépôt et le 1er janvier qui suit immédiatement). Suivent alors des capitalisations annuelles pendant n années et enfin une dernière capitalisation lors du retrait, qui s'effectue une durée décimale d2 plus tard. Dans les faits, sont connus le capital initialement placé C0, sa valeur acquise C(t) et la durée de placement t = d1 + n + d2. Pour estimer le rendement du capital, il faut calculer i. Mais une telle équation de degré n + 2 peut révéler plusieurs solutions, dont une seule est pertinente économiquement : celle qui estime le rendement du placement.
Le théorème des accroissements finis vient à la rescousse ! On transforme l'équation de départ en isolant dans le membre de droite le « i » apparaissant dans l'exponentielle (1 + i)n, de manière à construire l'équation de récurrence suivante :
Partant d'une valeur initiale arbitraire i0 bien choisie, on construit une suite de valeurs qui converge rapidement vers la solution. La dérivée (en valeurs absolue) de notre fonction particulière est bornée par 2 / n. Dès que la durée naturelle excède deux ans (n > 2), les conditions de convergence sont vérifiées. Le choix de la valeur initiale n'a que peu d'importance, pourvu que l'on ne s'écarte « pas trop » de la valeur cherchée, la méthode étant auto-correctrice. Un choix judicieux n'améliore que peu la vitesse de convergence, comme on peut le voir sur l'exemple présenté en encadré.
Le signe de la dérivée 
, par contre, influe sur la qualité de la convergence. Lorsque la dérivée est négative, la suite construite encadre progressivement la valeur cherchée, en formant une suite alternant les valeurs supérieures et inférieures et limitant ainsi d'emblée l'erreur entachant la solution retenue. Lorsque cette dérivée est positive, la suite construite croît ou décroît vers la solution, cumulant ainsi les erreurs et ne permettant que plus difficilement une mesure de l'erreur affectant la solution retenue. Dans notre exemple, cette dérivée est négative (grâce à la présence du polynôme en i au dénominateur de la racine) et tout se passe pour le mieux.
La théorie de la toile d'araignée
Ce cas de figure donne aussi naissance à ce que l'on nomme la théorie de la toile d'araignée, ou théorie du cobweb en économie. On s'intéresse à un système économique dont l'état à tout instant t est une fonction de son état à un instant antérieur :  = \phi(x(t_{k-1})).)
Sous quelles conditions le système étudié est-il « stable », c'est-à-dire va-t-il converger vers un état fixe 
? On le sait à présent, ce sera le cas dès que la dérivée de la fonction 
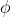
est (en valeur absolue) 
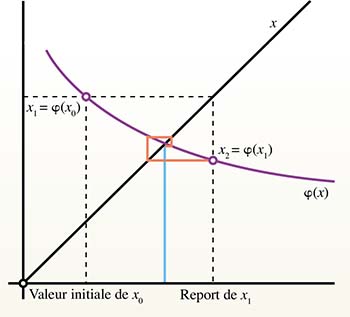
est décroissante, une représentation graphique de l'évolution du système justifie pleinement l'appellation de « toile d'araignée », une toile qui, loin de nuire au système ou de l'anéantir, en assure au contraire la stabilité à long terme : un rêve pour tout économiste ! On le constate, le cheminement vers l'intersection entre la fonction identité X et la fonction d'état  )
s'enroule littéralement autour de la situation d'équilibre.
est décroissante, une représentation graphique de l'évolution du système justifie pleinement l'appellation de « toile d'araignée », une toile qui, loin de nuire au système ou de l'anéantir, en assure au contraire la stabilité à long terme : un rêve pour tout économiste ! On le constate, le cheminement vers l'intersection entre la fonction identité X et la fonction d'état Lire la suite