Le théorème de Rolle, tout comme le fameux théorème des accroissements finis, a été déprogrammé de l'enseignement secondaire. Pour autant, ces deux résultats majeurs de l'analyse n'ont pas qu'une importance historique. Ils permettent de résoudre bien des questions mathématiques !

Des « cascades » de Rolle sont nés les grands théorèmes de l'analyse, qui non seulement fournissent des méthodes de démonstration, mais établissent de façon définitive le lien entre les variations d'une fonction et sa dérivée. Pour Rolle, qui s'est toujours méfié du « nouveau » calcul différentiel, a dénigré le livre du marquis de l'Hospital et entamé une polémique avec Varignon à ce sujet, c'est presque une revanche sur l'histoire de devoir sa notoriété à ce qu'il a tant combattu de son vivant…

 

Le mathématicien français Michel Rolle (1652-1719) se fit connaître en donnant en 1682 une solution à un problème posé par son contemporain Jacques Ozanam : « Trouver quatre nombres tels que la différence de deux quelconques soit un carré et que la somme de deux quelconques des trois premiers soit encore un carré. » L'auteur du problème lui-même prétendait que « le moindre de ces nombres n'a pas moins de cinquante figures [chiffres] » alors que Rolle a trouvé une solution à seulement sept chiffres : {2 399 057, 2 288 168, 1 873 432, 6 560 657}. Son secret ? Mettre le problème en équation avec des polynômes de degré allant jusqu'à 18 et encadrer leurs racines par une méthode de son invention, la fameuse méthode des cascades qu'il a décrite dans sa Démonstration d'une Méthode pour résoudre les Egalitez de tous les degrez (1691).

 

À l'origine, Rolle a établi une méthode pour résoudre une équation polynomiale qu'il énonce, d'abord sans le démontrer dans son Traité d'Algèbre de 1690, puis avec une preuve dans sa Démonstration de 1691. Son résultat ? Il s'énonce simplement : entre deux racines consécutives de f(x) il y a une racine d'une autre équation de degré moindre ; entre deux racines consécutives de cette dernière, il y a une racine d'une nouvelle équation de degré inférieur ; etc., poursuivant cette liste jusqu'à trouver un polynôme dont les racines soient faciles à calculer. Il nomme ces fonctions de degrés décroissants les cascades et il lui est aisé de remonter ensuite « en cascade » la liste de ces fonctions pour arriver à encadrer les racines du polynôme de départ. Mais que sont ces fameuses « cascades » ?

Mieux vaut illustrer la démarche par le polynôme défini par f(x) = x⁴ – 14x³ + 63x² – 106x + 56. Rolle suggère, pour former les « cascades », de « multiplier chaque terme de l'équation par l'exposant de l'inconnue et de diviser par l'inconnue », puis de « faire de même avec la seconde équation obtenue et de continuer jusqu'à obtenir une équation du premier degré ». N'est-ce pas là exactement un calcul de dérivées de tous ordres ?

Ayant obtenu successivement, avec les notations d'aujourd'hui, f'(x) = 4x³ –42x² + 126x – 106, f''(x) = 12x² – 84x + 126, f⁽³⁾(x) = 24x – 84, la méthode de Rolle, considérant qu'il est aisé de déterminer les racines de la dernière équation 24x – 84 = 0 (soit x = 3,5), conduit, de proche en proche, à trouver des bornes aux racines de chacune des équations précédentes, et ainsi finalement séparer celles de l'équation initiale f(x) = 0. En effet, l'une des racines, \( \alpha\) , de l'avant-dernier polynôme est inférieure à 3,5 (on peut même dire entre 1 et 3,5), l'autre,  \( \beta\) , au-delà de 3,5 (en fait entre 4 et 5), le polynôme précédent verra ses racines, pour l'une inférieure à \( \alpha\) (en fait entre 1 et \( \alpha\) ), pour l'autre entre \( \alpha\) et \( \beta\) (ici entre 3 et 4) et pour la dernière supérieure à \( \beta\) (en réalité entre 5 et 6). Ceci le mène à affirmer que les racines de l'équation de degré 4 proposée sont, pour la plus petite, inférieure à \( \alpha\) , pour la suivante entre \( \alpha\) et 3, la troisième entre 3 et 5 et la dernière au-delà de 6. Gagné, puisque ces racines sont précisément 1, 2, 4 et 7 (trop facile ! Mais les coefficients de Rolle étaient autrement plus compliqués…).

 

 

L'idée de la méthode des cascades est donc bien qu'entre deux racines consécutives de la dérivée on trouve au plus une racine réelle de la fonction. C'est cette même idée d'encadrer les racines qui va donner lieu au résultat qui, bien plus tard, en 1846, sous l'impulsion du mathématicien italien Giusto Bellavitis, portera le nom de théorème de Rolle. Il s'énonce habituellement sous la forme suivante :

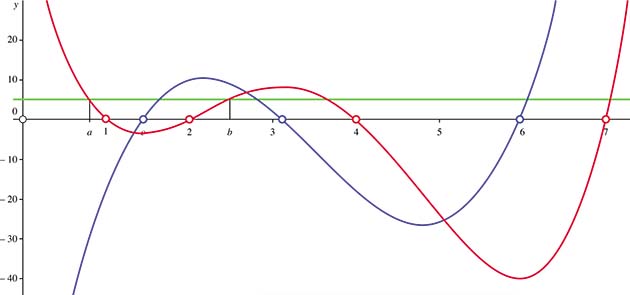
Si f est une fonction continue sur l'intervalle fermé [a, b], à valeurs réelles, et dérivable sur l'intervalle ouvert ]a, b[ telle que f(a) = f(b), alors il existe un nombre c dans ]a, b[ tel que f'(c) = 0.

Avec ces hypothèses, sur le schéma précédent, la courbe représentative de la fonction f (en rouge) admet une tangente en tout point de ]a, b[ et relie deux points A et B d'abscisses respectives a et b, de même ordonnée (voir la droite verte). Le théorème permet de conclure qu'il existe sur cet intervalle au moins un point, d'abscisse c, où la tangente est parallèle à (AB), c'est-à-dire horizontale.

La fonction f étant continue sur [a, b], elle est bornée et atteint ses bornes, m pour sa borne inférieure et M pour sa borne supérieure (m < M). Si m = M,  f est constante sur [a, b] et f' identiquement nulle sur ]a, b[. Ce cas étant écarté, m < f(a) ou f(a) < M. Dans ce dernier cas, par exemple, il existe c de 

]a, b[ tel que f(c) = M et alors, sur ]a, c[, f(x) < f(c), 

 et sur ]c, b[, f(x) < f(c), d'où

 

 La fonction f étant dérivable en c, par passage à la limite

 

Et nécessairement f'(c) = 0. On traite de la même façon le cas m < f(a).

Attention : toutes les hypothèses faites sur f sont nécessaires et le point à tangente horizontale n'est pas nécessairement unique ! Dans le polynôme précédent, qui vérifie bien toutes les hypothèses du théorème de Rolle, sur l'intervalle [0, 5], il existe plusieurs points à tangente horizontale.

 

 

Indissociable du théorème de Rolle, le théorème des accroissements finis en est une conséquence : on va se placer maintenant dans le cas d'une fonction  f vérifiant les mêmes hypothèses de continuité et de dérivabilité, mais telle que f(a) ne soit pas nécessairement égal à f(b), et évaluer l'accroissement (forcément fini) de f entre a et b.

Si f est une fonction continue sur l'intervalle fermé [a, b], à valeurs réelles, et dérivable sur l'intervalle ouvert ]a, b[, alors il existe un nombre c dans ]a, b[ tel que f(b) – f(a) = (b – a) f'(c).

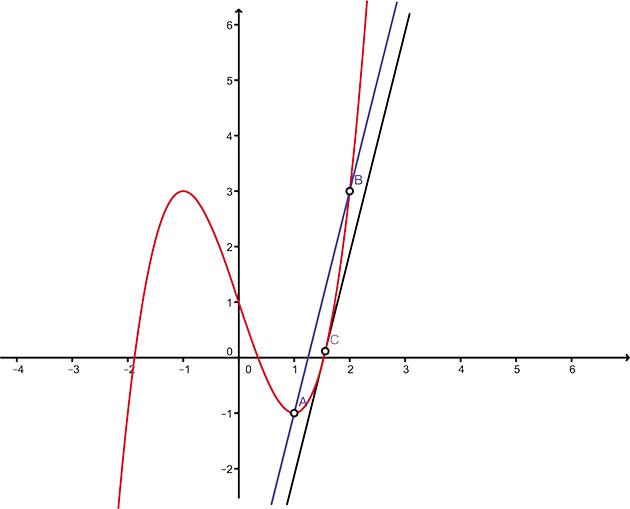
C'est le fameux théorème des accroissements finis ! Il ne dit rien d'autre que, même dans le cas où f(a) ≠ f(b), et si A(a, f(a)) et B(b, f(b)), il existe un point C distinct de A et de B où la tangente est parallèle à la droite (AB). Le tracé (voir le schéma) a été réalisé en considérant la fonction définie par f(x) = x³ – 3x + 1 sur l'intervalle [1, 2].

La démonstration se fait en appliquant le théorème de Rolle à la fonction u définie sur [a, b] par 

 

Ainsi,

  \( f'(c)=\frac{f(b)-f(a)}{b-a}\)

donc la tangente au point d'abscisse c à la courbe représentant f est bien parallèle à la droite passant par les points A(a, f(a)) et B(b, f(b)).

 

On peut alors utiliser ce résultat pour donner, sans trop se fatiguer, des approximations comme celle de, au hasard,  \( \sqrt{1652}\) . On sait que \( \sqrt{1652}\) est compris entre 40 et 41 (voir, dans notre dernier numéro, le dossier consacré aux racines !), mais encore ? Appliquons le théorème à la fonction racine carrée sur l'intervalle [1 600, 1 652] : il existe sur ]1 600, 1 652[ un réel c tel que \( \sqrt{1652}\) – \( \sqrt{1650}\) = (1 652 – 1 600) * 1/(2 \( \sqrt{c}\) ), d'où, comme 1 / 80 < 1/(2 \( \sqrt{c}\) ) < 1 / 81, on obtient rapidement : 40,63 < \( \sqrt{1652}\) < 40,65, encadrement que l'on peut encore raffiner en appliquant à nouveau le théorème, cette fois sur l'intervalle [1 652, (40,65)²]…

 

L'idée d'exploiter le théorème des accroissements finis pour donner lieu à des inégalités conduit de manière naturelle à l'inégalité des accroissements finis : si f est une fonction définie et continue sur [a, b], à valeurs réelles, dérivable sur ]a, b[ et qu'en plus, sur cet intervalle, sa dérivée soit bornée par m et M (m ≤ M), alors

La démonstration va de soi puisque la différence f(b) – f(a), qui s'écrit aussi, comme f est dans les hypothèses du théorème des accroissements finis, (b – a)f'(c) avec a < c < b, vérifie m(b – a) ≤ f(b) – f(a) ≤ M(b – a), d'où l'inégalité annoncée. Quelle cascade de résultats dus au théorème de Rolle !