De l'abaque au boulier, que de chemin parcouru pour arriver à notre algorithme actuel bien connu des écoliers.

 

L'algorithme le plus ancien utilisé pour diviser concerne l'abaque, un ancêtre du boulier. Il consiste à revenir à la définition même de la division euclidienne. Ainsi, la division de 201 par 13 consiste à retrancher 13 de 201 autant de fois que possible. Bien entendu, il serait fastidieux de procéder de cette manière. On essaye donc de retrancher un multiple de 13 plus important, dès le départ, par exemple 130, jusqu'à ce qu'on ne puisse plus le faire. La règle est simple en théorie mais délicate à appliquer ! À la fin, le quotient est 15 et le reste 6, quelle que soit la méthode utilisée.

 

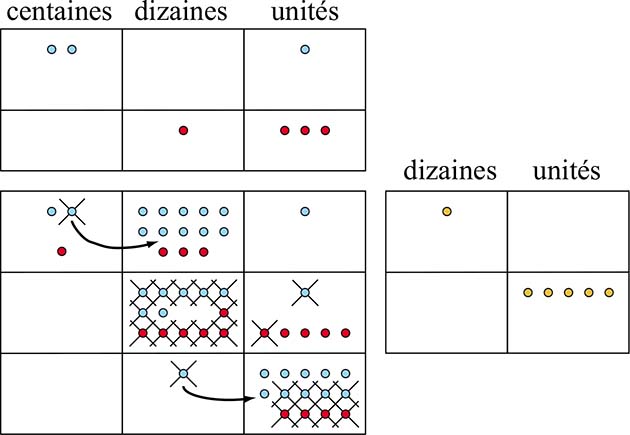
 Cet abaque est le plus élémentaire, le plus moderne, et est toujours utilisé de nos jours : il s'agit du boulier japonais (ou soroban).

 

L'idée de la division pratiquée dans l'Égypte ancienne, et toujours en Russie, est d'écrire le numérateur (201 ici) comme une somme de puissances de 2, ce qui revient à l'écrire en binaire. Ici : 201 = 128 + 64 + 8 + 1, et on distribue la division ainsi :

201 ÷ 13 = 128 ÷ 13 + 64 ÷ 13 + 8 ÷ 13 + 1 ÷ 13.

On effectue alors chaque division :

128 ÷ 13 = 9 + 11 ÷ 13, 64 ÷ 13 = 4 + 12 ÷ 13, ce qui donne :

201 ÷ 13 = 9 + 11 ÷ 13 + 4 + 8 ÷ 13 + 8 ÷ 13 + 1 ÷ 13.

On en déduit : 201 = 13 + 32 ÷ 13.

Comme 32 ÷ 13 = 2 + 6 ÷ 13, on obtient 201 ÷ 13 = 15 + 6 ÷ 13.

Le quotient de 201 divisé par 13 est donc 15 et le reste 6.

 

Voici comment la division de 201 par 13 se pose usuellement : on divise d'abord 20 par 13, le quotient est 1 et le reste 7, on recommence avec 71, le quotient est 5 et le reste 6.

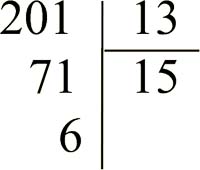
À partir de cet algorithme, on montre facilement que le développement d'un nombre rationnel, c'est-à-dire d'un quotient d'entiers, est périodique, car le nombre de restes possibles est fini. Par exemple, si on divise par 7, il n'existe que sept restes possibles : les chiffres de 0 à 6. L'un au moins se répète !

 

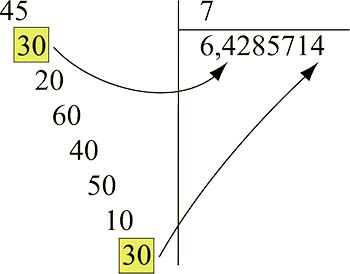
Par exemple, quand on divise 45 par 7, après un certain nombre de divisions, on trouve le même reste que la première fois. Les mêmes causes produisant les mêmes effets, les suites des quotients partiels et des restes sont alors identiques. Autrement dit :

 

 

Les décimales se reproduisent à l'identique tous les six chiffres, le développement décimal de 45 / 7 est donc périodique, de période 6. Ce phénomène n'est pas un cas particulier. De plus, la réciproque est vraie : si un développement est périodique, le nombre est rationnel !