Les logiciels graphiques comportent tous une instruction permettant de tracer un segment de droite. Pour relier deux points, il suffit donc de l'utiliser… Mais comment ces logiciels sont-ils construits ? La question a plus d'intérêt qu'il ne semble car le tracé d'un segment de droite est à la base de toutes les autres instructions graphiques !

Une grille de pixels

En négligeant la question des couleurs, l'écran d'un ordinateur est divisé comme une grille de bataille navale ou de mots croisés en un certain nombre de « points ». Dans le jargon de l'informatique, on parle de pixels. Le terme pixel vient de la contraction des termes anglais picture (« image » en anglais) et element. Il semble avoir été utilisé pour la première fois dans une publication de l'ingénieur américain Frederic Billingsley en 1965.

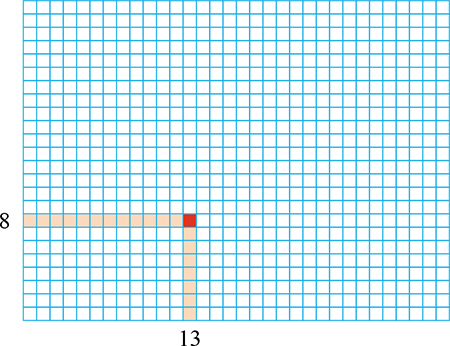Un point est repéré par deux nombres entiers. Ici, le point de coordonnées (13, 8) a été rougi. Chaque point intérieur de la grille possède huit voisins. Pour chacun de ces points, l'une au moins des coordonnées diffère d'une unité.


Le nombre de pixels varie suivant le mode de la carte graphique utilisée. De nos jours, il est courant d'utiliser une définition de 1 920 × 1 080, soit plus de deux millions de pixels. Chaque pixel est repéré par ses deux coordonnées, notées x et y selon l'usage. On dispose donc d'un point de départ M₀, de coordonnées (x₀, y₀), et l'on désire tracer sur l'écran le segment de droite le reliant au point d'arrivée M₁, de coordonnées (x₁, y₁). Plus précisément, chaque point peut être noirci ou non, et il s'agit de noircir tous les points du segment [M₀M₁].

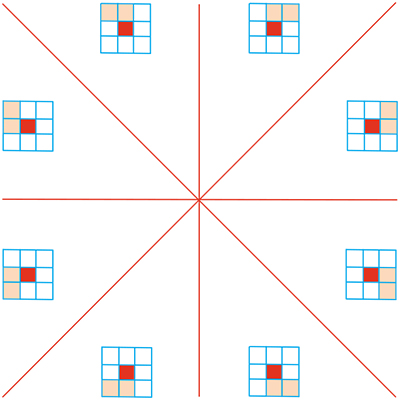Suivant la région où se situe le vecteur \( \overrightarrow{M_0M_1}\) , les seuls voisins à retenir ont été rosis.


Le mouvement se prouve en marchant ! Pour aller jusqu'à M₁, il faut d'abord quitter M₀. Le premier point à noircir est donc l'un des huit pixels voisins de M₀. Lequel ? La réponse est obtenue en visant M₁, d'où notre premier pas. Ensuite, comme en marchant, on récidive jusqu'à ce que l'on ait atteint le but, c'est-à-dire M₁. En informatique, une telle méthode est dite récursive. Chaque point possède huit voisins, mais comme la direction  est connue, deux seulement sont à retenir à chaque pas, comme le montre la figure suivante centrée en M₀.

Pour déterminer la zone à conserver, il suffit de trois tests. Pour les effectuer, on calcule d'abord les accroissements des coordonnées entre les deux points : h = x₁ – x₀ et k = y₁ – y₀. Les trois tests à faire sont alors :

1. Tester si h > 0, ce qui permet de situer la zone à gauche ou à droite de l'axe vertical,

2. Tester si k > 0, ce qui permet de situer la zone à gauche ou à droite de l'axe horizontal,

3. Tester si |h| > |k|, ce qui permet de situer la zone par rapport aux axes diagonaux.

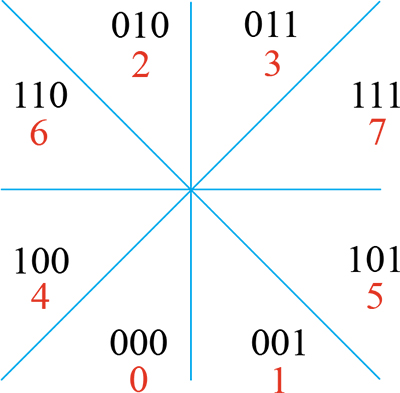Les réponses à ces tests sont 0 ou 1 (0 pour « faux » et 1 pour « vrai »). Elles peuvent donc être assemblées en un nombre de trois chiffres binaires. Par exemple, 101 signifie h > 0, k ≤ 0 et |h| > |k|. Chaque nombre binaire correspond ainsi à la zone indiquée sur la figure suivante.

Des droites en escalier

À chaque zone correspondent deux points possibles selon la figure précédente. Par exemple, à la zone 4, il ne peut correspondre qu'un point des zones 4 ou 0. Ils sont donnés par les accroissements de leurs coordonnées (h₁, k₁) et (h₂, k₂) dans le tableau suivant :

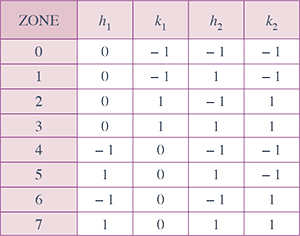
À ce stade, à chaque pas, il ne reste qu'à choisir entre deux points. Lequel ? Bien entendu, le plus raisonnable est de retenir le point « le plus proche » de la droite à tracer, c'est-à-dire celui qui minimise la valeur absolue de l'expression k (x – x₀) – h (y – y₀), puisqu'un point appartient à la droite si, et seulement si, il annule cette expression. L'algorithme de tracé d'une droite est maintenant bien cerné (une transcription précise est présentée en encadré). Dans la pratique, il donne un segment de droite en escalier, ce qui ne se voit pas à l'œil nu si la taille des pixels est suffisamment petite.