Admirons le peintre de la Renaissance à son ouvrage. Imaginons cette situation représentée de profil dans le plan muni d'un repère orthonormé. Comme sur le schéma ci-dessous, on peut imaginer que l'œil de l'artiste est situé en l'origine et que la toile du maître est située sur la droite d'équation x = 1, parallèle à l'axe des ordonnées.

Si la toile est infinie, tout point A du plan peut être projeté sur un point A' de la toile. On peut même observer que tous les points situés sur une même droite passant par O sont projetés sur le même point de la toile. Ainsi, toute droite du plan passant par l'origine correspond à un unique point de la droite d'équation x = 1. Toutes ? Non ! Une droite résiste encore : l'axe des ordonnées. Qu'à cela ne tienne, ajoutons un nouveau point à notre droite-toile : un point « à l'infini », qui correspond intuitivement à l'endroit où se couperaient l'axe des ordonnées et la droite d'équation x = 1. Et c'est ainsi que les travaux des peintres sur la perspective nous offrent un nouveau point de vue sur la géométrie du plan !

Un nouveau point… de vue

Plus généralement, si l'on considère un plan vectoriel E, la droite projective est l'ensemble des droites vectorielles de E. D'un point de vue un peu plus technique, est l'ensemble des classes d'équivalence de   sous la relation d'équivalence de colinéarité.

Voici un nouveau terrain de jeu pour la géométrie. Quelles sont donc les applications de la droite projective dans elle-même qui pourraient s'avérer fécondes ? Considérons déjà les applications du plan vectoriel initial dans lui-même qui passeront aisément la phase de projection sur la toile du peintre. Ces transformations vectorielles ne sont rien d'autre que les isomorphismes du plan. Les applications ainsi obtenues sur la droite projective sont les homographies.

Pour décrire ces homographies, commençons par nous repérer sur cette nouvelle droite. Reprenons notre exemple et considérons les droites d₁ et d₂ d'origine O et de vecteurs directeurs respectifs  et . Comme  et   sont colinéaires, les droites d₁ et d₂ sont confondues et correspondent donc au même point M de la droite projective. On peut ainsi attribuer des coordonnées à ce point, celles des vecteurs ou par exemple, mais elles ne sont définies qu'à un coefficient multiplicateur près ! C'est ce que l'on appelle les coordonnées homogènes du point M. On les note (3 : 2), ou encore (6 : 4).

Deux coordonnées pour un point d'une droite, voilà qui peut sembler curieux. Il n'est cependant pas difficile de se ramener à une situation plus classique en considérant le quotient de ces deux coordonnées. Ainsi, l'abscisse projective de M est . Si jamais la seconde coordonnées est nulle, le quotient vaut alors  ; on retrouve bien l'idée initiale consistant à ajouter un point « à l'infini ».

Avec l'abscisse projective, l'étude des homographies se simplifie grandement : ce sont les applications h de la forme   avec ad – bc ≠ 0

 
Le rapport des rapports : toute une harmonie

Comme toujours, les mathématiciens aiment chercher des invariants, ce qui ne change pas quand on applique certaines transformations. Pour ce qui est des homographies, l'invariant concerne le rapport que peuvent entretenir entre eux quatre points de la droite projective.

Une homographie de la droite projective est complètement définie par les images de trois points distincts (voir en encadré). En particulier, il n'existe qu'une seule homographie h qui envoie les points d'abscisses projectives a, b et c sur , 0 et 1 respectivement. Le birapport des points a, b, c et d est alors l'image de d par h. On note cela [a, b, c, d] = h (d).

Lorsque ce birapport est égal à – 1, on dit que les quatre points sont en division harmonique. C'est en particulier le cas si c est le milieu du segment [ab] et si d est le point à l'infini, ce qui est assez commode pour faire le lien entre des propriétés projectives et des propriétés de géométrie classique.

La force du birapport consiste en la simplicité de son expression et son invariance par l'application de toute homographie.

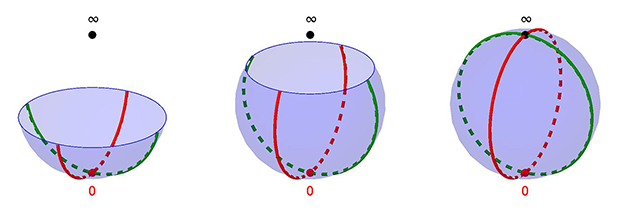
L'analogie avec la toile du peintre nous a implicitement guidés vers une construction de la droite projective réelle. Mais que se passe-t-il si le plan vectoriel initial n'est autre que  ? La démarche est identique : on ajoute un point à l'infini à la droite complexe, que nous voyons souvent comme un plan. Ainsi, la droite projective complexe \( \mathbb{P}(\mathbb{C}^2)}\) est souvent appelée… sphère de Riemann. La droite projective réelle n'est alors rien d'autre qu'un méridien de cette sphère, c'est-à-dire un cercle !

Les applications des nombres complexes à la géométrie plane sont bien connues. Le point de vue projectif, en ajoutant un point à l'infini, est encore plus stupéfiant ! Par exemple, le fait que quatre points du plan complexe soient alignés ou cocycliques revient à dire que leur birapport est réel. Une condition aussi simple a des retombées sensationnelles !

Le birapport de quatre points est un nombre complexe ou 3 mais un petit calcul montre que le produit des six birapports [a, b, r, s], [b, c, p, s], [c, a, q, s], [p, q, c, d], [q, r, a, d] et [r, p, b, d] vaut toujours 1. Il faut et il suffit donc que cinq de ces birapports soient réels pour que le sixième le soit également ! Voyons tout de suite un exemple avec le théorème de Simson.

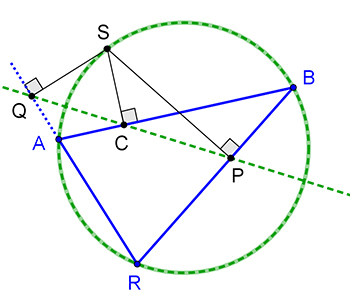
On considère un triangle ABR et un point S. On note P, Q et C les projetés orthogonaux de S sur les côtés de ABR. Comme BCS et BPS sont deux triangles rectangles de même hypoténuse, B, C, P et S sont cocycliques et [b, c, p, s] est réel. De même, [c, a, q, s] est réel. Ainsi, en notant D le point à l'infini, Q, C et P sont alignés si, et seulement si, S appartient au cercle circonscrit à ABR !

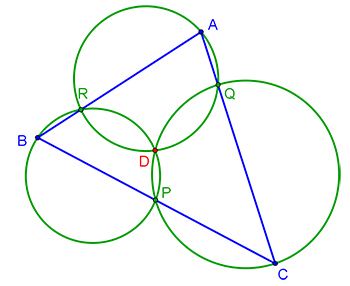Toujours sur le même principe, on peut démontrer que, si P, Q et R sont trois points des côtés d'un triangle ABC (comme indiqué sur la figure), alors les cercles circonscrits à ARQ, BPR et CQP possèdent un point commun D ! Il suffit d'appliquer le même résultat en notant S le point à l'infini.

Terminons sur un fabuleux résultat, dont la démonstration est étonnante de simplicité si on le regarde dans la droite projective complexe : le théorème de Miquel.

Considérons les huit points d'intersection A, B, C, D, P, Q, R et S de quatre cercles. Les points C, A, Q et S sont cocycliques si, et seulement si, R, P, B et D le sont aussi !

Qui aurait cru que voir une sphère comme une droite aurait permis d'établir de façon si élégante d'aussi spectaculaires résultats ?