Pour déterminer le plus court chemin d'un point à un autre sur un plan, il suffit de disposer d'une règle et de tracer la droite qui les joint. Le problème n'est pas plus compliqué dans le cas des surfaces développables, qui, comme les cylindres, les cônes ou le ruban de Möbius, peuvent être mis à plat sans déchirement ni étirement, donc sans que les distances soient modifiées. Pour déterminer le plus court chemin, il suffit d'« aplatir » la surface et de tirer un trait avec une règle.

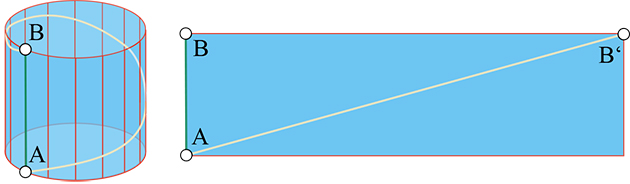
Aplatissement d'un cylindre pour déterminer ses géodésiques. On obtient des cercles (les directrices, en orange), des hélices (en jaune), et des droites (les génératrices, en rouge).

Dans le cas du cylindre, chaque point peut être représenté plusieurs fois, ce qui donne plusieurs courbes possibles a priori. Toutes sont appelées des géodésiques, même si une seule d'entre elles réalise le plus court chemin, car elles ont une propriété commune. Elles correspondent aux positions que prend un élastique tendu entre les deux points, à condition que la surface soit dépourvue de frottement et que l'on néglige la pesanteur. Mathématiquement, les géodésiques se caractérisent par une condition différentielle qui équivaut, lorsque la courbe est plane, à ce que, en tout point, son plan soit perpendiculaire au plan tangent à la surface en ce point (voir en encadré).

Parallèles et postulat d'Euclide

Si on appelle « droites » d'une surface ses géodésiques, on perd certaines propriétés habituelles de nos droites usuelles. Dans le cas du cylindre, par exemple, par deux points il peut passer plusieurs droites distinctes. En revanche, la définition du parallélisme dégagée par Euclide garde un sens : deux droites sont parallèles si elles n'ont aucun point commun. Il est alors légitime de se demander si le postulat d'Euclide, selon lequel par tout point il passe une et une seule droite parallèle à une droite donnée, est valide dans ce cadre ou non. Dans le cas du cylindre, ce résultat est exact puisque les géodésiques correspondent aux droites quand on développe le cylindre.

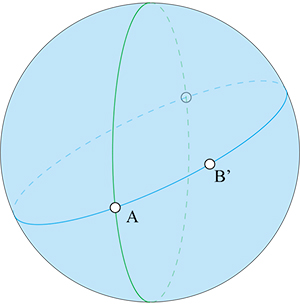
La sphère n'étant pas développable, on ne peut raisonner comme pour le cylindre. Cependant, la propriété physique liée à l'élastique reste valable. Elle permet d'imaginer que si deux points A et B d'une sphère sont « suffisamment proches » (en fait non antipodaux), alors le plus court chemin entre A et B existe et est unique. Supposons qu'il en soit ainsi. Considérons alors le plan AOB, où O est le centre de la sphère, et s la symétrie par rapport à ce plan. Soit Γ la géodésique allant de A à B. La courbe s (Γ) a même longueur que Γ et va également de A à B. L'unicité de la géodésique assure que s (Γ) = Γ, donc que Γ est incluse dans le plan AOB. Il s'agit d'un arc du grand cercle passant par A et B. Les géodésiques de la sphère sont donc les grands cercles. Ces courbes réalisent bien la condition différentielle citée en encadré puisqu'elles sont planes et que leurs plans sont perpendiculaires à la surface. Ce résultat est utile en navigation aérienne ou maritime, ou même pour s'orienter dans la direction d'un point de la Terre.

Sur une sphère, deux grands cercles se coupent toujours (en deux points antipodaux). Autrement dit, deux droites ne sont jamais parallèles ! Sur une telle surface, le postulat d'Euclide est donc faux. Plus précisément, par un point, il ne passe aucune parallèle à une droite donnée.

Sphère, cylindre et hyperboloïde

Les résultats concernant le cylindre et la sphère ne doivent pas faire penser que les géodésiques sont toujours aussi simples à décrire ou à caractériser. En fait, cela est très rarement le cas. Prenons l'exemple de l'hyperboloïde de révolution à une nappe. Les génératrices ainsi que les méridiennes sont des géodésiques. De plus, le cercle parallèle de rayon minimal en est une autre, ce qui fournit quatre géodésiques simples passant par les points de ce cercle. La construction de l'hyperboloïde à partir du cylindre amène à penser que certaines géodésiques se comportent comme celles du cylindre, en s'enroulant autour de l'hyperboloïde, ce qu'il est possible de vérifier. Le cercle parallèle de rayon minimal joue alors un rôle de frontière en décomposant l'hyperboloïde en une partie supérieure et une partie inférieure.

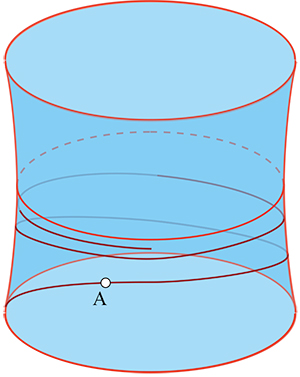Si un point A et un angle  entre 0 et π / 2 sont donnés, il existe une et une seule géodésique passant par A telle que la tangente en A fasse l'angle avec le cercle parallèle passant par A. De plus, il existe une valeur ₀ de en dessous de laquelle la géodésique reste dans la partie inférieure de l'hyperboloïde. Au-dessus de cette valeur, elle coupe le cercle limite et passe de l'autre côté. On en déduit facilement que le postulat d'Euclide n'est pas vérifié, le nombre de parallèles étant infini !