D'après le théorème de Bachet, si deux entiers relatifs a et b sont donnés et d est leur plus grand diviseur commun (ou pgcd), il existe deux entiers relatifs u et v tels que au + bv = d. Ce théorème se généralise aux polynômes car leur ensemble est également muni d'une division euclidienne. L'idée pour le démontrer est de considérer l'ensemble des polynômes de la forme A U + B V et, plus précisément, son élément de degré minimal, dont on démontre qu'il s'agit du pgcd de A et B (voir l'encadré). Cette démonstration débouche sur un algorithme de calcul consistant, à partir d'un polynôme de la forme A U + B V, à en déduire un autre, de degré inférieur, et à recommencer tant que cela est possible.

Prenons un exemple pour décrire l'algorithme d'Euclide permettant de déterminer un couple (U, V) tel que le degré de U soit strictement inférieur à celui de B, et le degré de V strictement inférieur à celui de A. Soit A = 3X³ + 2X² + 2 et B = X² – 2. En divisant A par B, on obtient : A – B (3X + 2) = 6X + 6 puis, en divisant B par X + 1 : B = (X + 1)(X – 1) – 1. On en déduit la relation de Bézout suivante :

\( A (X-1) + B (-3X^2 + X-4) = 6.\)

On en tire que le pgcd de A et B est égal à 1, c'est-à-dire que A et B sont premiers entre eux.

L'arrivée des éléments simples

De façon générale, d'après le théorème de Bézout, si A et B sont deux polynômes premiers entre eux, on peut trouver deux polynômes U et V tels que A U + B V = 1. La fraction rationnelle

\( \frac{1}{AB}=\frac{V}{A}+\frac{U}{B}\)

  peut alors s'écrire \( \frac{1}{AB}\) , où les degrés des numérateurs sont strictement inférieurs à ceux des dénominateurs. Dans le cas qui précède, on obtient :

\( \frac{6}{(3X^3+2X^2+2)(X^2-2)}= \frac{X-1}{X^2-2}+\frac{-3X^2+X-4}{3X^3+2X^2+2}.\)

De même, une fraction rationnelle telle que

\( \frac{3X^3}{(X-1)(X+1)(X-2)}\)

se décompose en un polynôme plus des éléments simples de la forme  \( \frac{A}{X-a}\) . Dans ce cas, on obtient :

\( \frac{3X^3}{(X-1)(X+1)(X-2)}=3-\frac{3}{2(X-1)}-\frac{1}{2(X+1)}+\frac{8}{(X-2)}.\)

Ce résultat algébrique peut sembler une fantaisie calculatoire sans grand intérêt. En fait, son intérêt essentiel se situe dans un autre domaine, en calcul intégral plus précisément. Par exemple, de la décomposition précédente, on déduit :

\( \int\frac{3x^3dx}{(x-1)(x+1)(x-2)}=3x-\frac{3}{2}\ln{|x-1|}-\frac{1}{2}\ln{|x+1|}+8\ln{|x-2|}+C\)

où C est une constante arbitraire, égalité qui a un sens sur les intervalles ne contenant aucun des points –1, 1 et 2.

Le calcul d'une telle décomposition est particulièrement simple dans le cas d'une fraction rationnelle n'ayant que des pôles simples. Dans ce cas en effet :

\( \frac{P}{Q}=R+\frac{A}{X-a}+\frac{B}{X-b}+...+\frac{K}{X-k}\)

où R est le quotient de P par Q, a, b… k sont les zéros de Q et A, B… K sont des nombres qu'il est aisé de calculer (voir l'encadré).

Le lien avec la géométrie

Le théorème de Bézout permet également d'étudier l'intersection de courbes algébriques, c'est-à-dire dont les équations sont des polynômes de x et y. Le cas le plus simple est celui de deux droites (équations de degré 1). Sauf si elles sont confondues, elles ont toujours un et un seul point d'intersection… si l'on considère que deux droites parallèles se coupent à l'infini.

Deux droites non confondues se coupent en un point unique, situé à l'infini si elles sont parallèles.

Ensuite, on peut envisager l'intersection d'une conique (équation de degré 2) et d'une droite (équation de degré 1), par exemple la parabole d'équation y – x² = 0 et les droites d'équations y – a = 0.

L'intersection de la parabole d'équation y – x² = 0 et de la droite d'équation y – a = 0 est constituée de deux points réels si a > 0, d'un point double si a = 0 (la droite est alors tangente à la parabole) et de deux points imaginaires si a < 0.

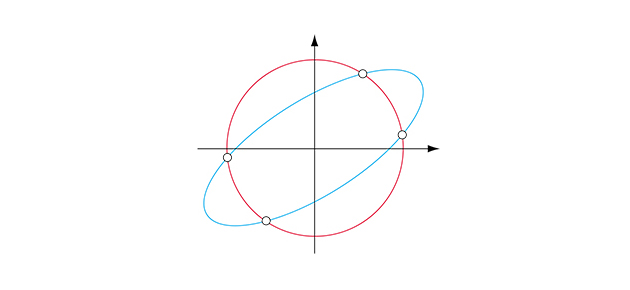
Envisageons maintenant l'intersection de deux coniques, par exemple le cercle d'équation x² + y² – 9 = 0 et l'ellipse d'équation x² + 2 y² – 2xy – 7 = 0. Un dessin permet de penser que leur intersection est constituée de quatre points.

L'intersection d'un cercle et d'une ellipse est constituée de quatre points.

Le théorème de Bézout permet de le démontrer si on l'applique aux deux polynômes (de la variable x) A = x² + y² – 9  et B = x² + 2y²  –2 xy – 7. En effet, l'identité de Bézout s'écrit alors :

\( (-2 xy + 3y^2 - 2) A + (2 xy + y^2 + 2) B= 5y^4 - 32 y^2 + 4.\)

Donc les points intersections du cercle et de l'ellipse vérifient 5y⁴ – 32 y² + 4 = 0, équation qui a quatre solutions. On en déduit que le cercle et l'ellipse ont quatre points d'intersections. Ce résultat se généralise à deux coniques, qui ont toujours quatre points d'intersection si elles ne sont pas confondues… à condition de compter les points imaginaires comme les points réels, deux fois les points doubles (où elles sont tangentes) et les points à l'infini ! Autrement dit, la question ne prend un sens précis que dans le cadre de la géométrie projective complexe, qu'il est impossible de présenter dans le cadre de ce dossier.

Ce résultat se généralise aux cas de deux courbes de degrés m et n dont l'intersection ne contient pas une courbe algébrique : l'intersection est alors constituée de mn points, à condition de compter les points à l'infini ainsi que les points imaginaires, et de compter leurs ordres de multiplicité.