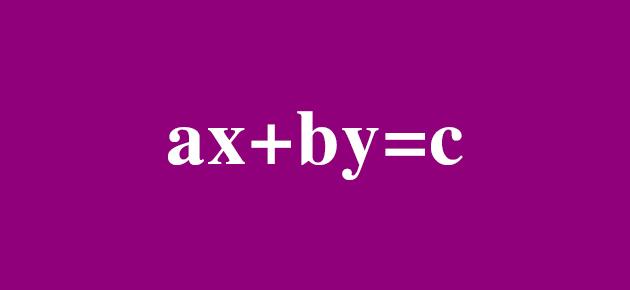
Claude-Gaspard Bachet de Méziriac fut un grand créateur de jeux et énigmes mathématiques. Il fait preuve dans son ouvrage phare Problèmes plaisants et délectables d'une ferveur constante pour l'arithmétique. Plusieurs de ces problèmes consistent à deviner un ou des nombres pensés, ils sont déclinés aussi sous forme de problèmes de cartes à jouer qu'un joueur doit choisir mentalement. On trouve également des problèmes de transvasement, de traversées, de poids et de monnaie et même une règle de construction des carrés magiques d'ordre impair. Cependant, Bachet n'est pas qu'un arithméticien. Il nous a laissé d'innombrables « astuces » en termes de mathématiques récréatives, comme cette façon très imagée de construire des carrés magiques. Le dessin ci-contre parle de lui-même.

 Un théorème, ça se démontre !

Mais revenons à l'arithmétique, et au résultat qui nous intéresse. Ce que l'on pouvait prendre, chez Bachet comme chez Bézout, pour une démonstration de « leur » théorème était plutôt un algorithme, une construction effective des solutions de l'équation en nombres entiers ax + by = 1, où a et b sont des entiers premiers entre eux. On peut fournir une preuve moins constructive mais plus « ramassée ».

Déjà, si a et b sont premiers entre eux, notons E l'ensemble des entiers naturels de la forme au + bv où u et v sont des entiers relatifs. E, contenant au moins a ou son opposé, n'est pas vide. Il a donc un plus petit élément c, lui aussi de la forme c = ax + by où x et y sont deux entiers relatifs. Effectuons la division avec reste de a par c (de quotient q et reste r) : a = cq + r avec r entier, 0 ≤ r < c. Ainsi, r = a – cq = a (1 – xq) + b(– yq) est aussi combinaison linéaire de a et b, donc fait partie de E. Étant strictement inférieur à c, plus petit élément de E, r, est nul, et donc a est divisible par c. On prouve de même que b est divisible par c, qui est donc un diviseur commun à a et b. Ces derniers étant premiers entre eux, la seule possibilité est que c = 1. Ainsi, il existe un couple (x, y) d'entiers relatifs tels que ax + by = 1. Astucieux, non ?

Réciproquement, s'il existe un couple (x, y) d'entiers relatifs tels que ax + by = 1, et si d est le plus grand commun diviseur de a et b, d divisera ax + by, qui est égale à 1. L'entier d divisera donc 1 ; c'est dire que d = 1, ou encore que a et b sont premiers entre eux.

L'identité de Bézout découle immédiatement du théorème homonyme : soient a et b deux entiers relatifs dont d est le plus grand commun diviseur. En divisant chacun d'eux par d, on obtient deux entiers a' (égal à a / d) et b' (égal à b / d) premiers entre eux. D'après le théorème précédent, il existe donc un couple (x, y) d'entiers relatifs tels que a'x + b'y = 1, d'où, en multipliant par d, ax + by = d.

Oui, mais en pratique…

On peut, concrètement, déterminer par un algorithme simple, les coefficients x et y de l'identité ax + by = d, si a et b sont deux entiers relatifs et d leur plus grand commun diviseur. Traitons le cas a = 3 219 et b = 1 813. On détermine déjà par l'algorithme d'Euclide que d = 37 en dressant le tableau des quotients et des restes successifs (on divise 3 219 par 1 813 : quotient q, reste r, puis 1 813 par r, etc., en divisant à chaque étape le diviseur, qui est le reste précédent, par le reste suivant ; d est le dernier reste non nul). On recherchera en même temps x et y en écrivant que les restes successifs sont combinaison linéaire de 3 219 et 1 813. L'algorithme peut être visualisé sur le tableau des restes et des quotients successifs : 

On obtient au final x'' = x – q''x', y'' = y – q''y'.  Dans notre cas, le dernier reste non nul est d = 37, et l'on trouve 3 219 × (– 9) + 1 813 × 16 = 37.  À vous de jouer !

Le théorème de Bachet – Bézout a de multiples conséquences, qui donneront lieu aux grands théorèmes de l'arithmétique. Le théorème de Gauss, démontré dans son ouvrage Disquisitiones arithmeticae (1801), est l'un d'eux : si a, b et c sont trois entiers et que a divise le produit bc tout en étant premier avec b, alors il divise c.

La preuve repose sur le théorème de Bézout. En effet, a et b étant premiers entre eux, leur plus grand commun diviseur est égal à 1. Il existe donc deux entiers u et v tels que au + bv = 1. D'où en particulier auc + bvc = c. Or a divise bc, donc bc = aq, et ainsi auc + avq = c, ou encore a (uc + vq) = c. C'est donc que a divise c.

On trouve la première trace d'un remarquable résultat, le théorème (des restes) chinois, dans le Sunzi suanjing (Classique mathématiques de maître Sun, composé entre le III^e et le V^e siècles avant notre ère). Il est posé sous une forme simple : « Soient des objets en nombre inconnu. Si on les range par trois, il en reste 2. Si on les range par cinq, il en reste 3 et si on les range par sept, il en reste 2. Combien y a-t-il d'objets ? »
En d'autres termes, il s'agit de résoudre le système :

\( \left \{ \begin{array}{l} x\textrm{ a m\^{e}me reste que }a\textrm{ dans la division par }m,\\ x\textrm{ a m\^{e}me reste que }b\textrm{ dans la division par }n. \end{array} \right.\)

Le résultat est alors que si m et n sont premiers entre eux (et supérieurs à 2), pour tout couple d'entiers (a, b), ce système admet des solutions entières, deux solutions quelconques différant d'un multiple de mn. La démonstration, constructive, utilise notre résultat fétiche (voir en encadré).

Arithmétique : aucun problème !

Connaître le théorème de Bachet – Bézout, c'est aussi savoir résoudre une équation diophantienne simple, du type Ax + By = C, où A, B et C sont des entiers relatifs. C'est comme si vous vouliez trouver combien il y a de façons d'écrire 73 comme somme d'un multiple de 3 et d'un multiple de 5.

Si C n'est pas un multiple de d, le plus grand commun diviseur de A et B, alors l'équation n'a pas de solution. En effet, d devant diviser Ax + By, il devrait aussi diviser C, ce qui n'est pas. Dans le cas général, on se ramène, en divisant par d, à une équation où les coefficients sont premiers entre eux : ax + by = c (avec a = A / d, b = B / d et c = C / d). D'après l'identité de Bézout, il existe deux entiers u et v tels que au + bv = 1. Il vient, après multiplication par c, que le couple (x₀, y₀) = (cu, cv) est une solution particulière. Par soustraction :

  \( \frac{- \left \{ \begin{array}[l]{l} ax+by=c \\ ax_0+by_0=c \end{array} \right. }{a(x-x_0)=-b(y-y_0)}\)

C'est dire que b doit diviser a (x – x₀) et comme il est premier avec a, il devra diviser x – x₀ (théorème de Gauss), d'où x – x₀ = kb. Il s'ensuit que y – y₀ = – ka. Les solutions de l'équation de départ seront donc toutes données par x = x₀ + kb, y = y₀ – ka.

Et pour notre petit problème ? Il s'agit de résoudre en nombres entiers l'équation 3x + 5y = 73. Une solution particulière évidente est x = 21, y = 2. Les solutions sont donc données par x = 21 + 5k, y = 2 – 3k. Le problème a, en nombres positifs, cinq solutions, les couples (21, 2), (16, 5), (11, 8), (6, 11) et (1, 14).