L'énoncé qui a fait passer Bézout à la postérité prend soit la forme d'un théorème dit de Bachet–Bézout (a et b étant deux entiers relatifs, a et b sont premiers entre eux si, et seulement si, il existe deux entiers relatifs x et y tels que ax + by = 1), soit celle d'une identité (il existe deux entiers relatifs x et y tels que ax + by = d, avec d le plus grand commun diviseur de a et b). L'identité se déduit facilement du théorème. Le résultat n'est cependant un « scoop » pour aucun des deux mathématiciens aux noms associés, mais le premier l'a démontré à sa manière et le second l'a généralisé.

Bachet, le précurseur

Bachet de Méziriac pratiquait aussi bien la poésie que les langues anciennes ou les mathématiques, mais c'est essentiellement par ses Problèmes plaisants et délectables qui se font par les nombres (voir en encadré) et par les méthodes de résolution qu'il propose que nous le connaissons aujourd'hui.

L'idée sous-jacente à cet ouvrage est novatrice : les récréations mathématiques étaient reléguées habituellement en annexe et elles sont ici l'objet même du livre. L'auteur y explique de façon détaillée ses propres méthodes de résolution, souvent originales. Ce ne sont pas des problèmes amusants qui viennent illustrer des théorèmes sérieux, mais des problèmes récréatifs qui conduisent à chercher des mathématiques utiles pour les résoudre.

C'est dans ce cadre que l'on rencontre des problèmes conduisant à résoudre des équations linéaires en nombres entiers, problèmes qui n'étaient pas originaux lorsque Bachet les publia. Beaucoup trouvent leur origine dans la tradition médiévale des « problèmes des cent volailles » des mathématiciens chinois, indiens ou arabes, que cite par exemple Abu Kamil à la fin du IX^e siècle : « Un canard de 5 dirhams, vingt oiseaux pour 1 dirham et un poulet de 1 dirham. On t'a payé 100 dirhams et on t'a dit : “Achète avec cela cent volatiles de ces espèces.” » Bachet en donne, lui, ses propres énoncés et, selon sa méthode, utilise une note pour exposer un principe de résolution d'une équation du premier degré à deux inconnues. Il donne même, au début de la seconde édition de ses Problèmes plaisants et délectables, une quasi-démonstration du théorème que reprendra Bézout. L'énoncé figure entre autres sous la forme suivante : « Deux nombres premiers entre eux étant donnez, trouver le moindre multiple de chacun d'iceux surpassant de l'unité un multiple de l'autre » et la démonstration, sur plusieurs pages, s'avère longue et compliquée.

Des problèmes amusants aux problèmes récréatifs

Voici un exemple illustrant la méthode de Bachet pour résoudre l'épineuse question de trouver le premier multiple de 211 qui surpasse de 10 un multiple de 1 007 (en d'autres termes, il s'agit de trouver la plus petite solution de l'équation 211x = 1 007y + 10).

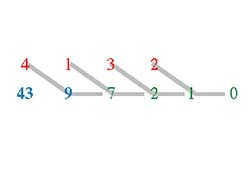
Bachet divise d'abord A (= 1 007) par B (= 211) : quotient 4, reste 163 ; puis il divise 211 par 163, comme dans l'algorithme d'Euclide utilisé pour déterminer le plus grand commun multiple : quotient 1, reste 48. Et il continue ainsi… jusqu'à obtenir un reste égal à 10. Pour récupérer le premier multiple de B qui surpasse de 10 un multiple de A, il exprime méticuleusement E en fonction de D : 2E = 1 × D – 10, puis D en fonction de C (7D = 2C + 10)… et enfin B en fonction de A : 43B = 9A + 10. La solution du problème est donc 43 × 211 = 9 × 1 007 + 10.

Soucieux du bien-être calculatoire des utilisateurs de sa méthode, Bachet invente une disposition astucieuse pour arriver au résultat sans reconstituer tous ces calculs. Il recopie les quotients dans l'ordre sur une ligne (en rouge), écrivant sur une deuxième ligne, à droite du dernier quotient, le nombre 1, puis calculant : 1 × 2 + 0 = 2. On écrit 2 à gauche du 1. Puis on calcule 2 × 3 + 1 = 7, on écrit 7 à gauche du 2, etc. jusqu'à finalement obtenir : 9 × 4 + 7 = 43.

La méthode Bézout : éviter les « mots qui fâchent »

Bézout, à travers ses livres, est surtout connu comme algébriste, spécialiste ès équations, mais sa méthode de recherche est inhabituelle pour son temps. Il traite des problèmes d'ordre tout à fait général sans utiliser un gros déballage de matériau mathématique : son originalité est d'attaquer le problème à travers des cas particuliers que chacun sait résoudre. C'est là qu'intervient son expérience d'enseignement à des non-mathématiciens. Il va par exemple traiter la géométrie avant l'algèbre, simplement parce qu'il sait que les débutants, pas très familiers avec la démonstration algébrique, comprennent mieux les preuves géométriques. Il va éviter les « mots qui fâchent » : axiome, théorème, lemme, corollaire, scholie, jugeant, dans la droite ligne de d'Alembert, que « l'usage de ces mots n'ajoute rien à la clarté des démonstrations » et que cela peut même égarer les débutants « en les persuadant qu'une proposition revêtue du nom de théorème doit être une proposition aussi éloignée de leurs connaissances que le nom l'est de ceux qui leur sont familiers ». Son approche d'un problème par des cas particuliers amène à comprendre de mieux en mieux le cas général : c'est sa méthode de « simplification des hypothèses ».

L'identité heureuse

Préférant toujours la pratique sur des exemples à l'exposé théorique, Bézout utilise dans son Cours d'algèbre de 1766 la résolution en nombres entiers d'une équation linéaire à deux inconnues pour introduire le résultat qui, beaucoup plus tard, portera le nom d'identité de Bézout. C'est en effet en 1949, par un choix de l'équipe Bourbaki, groupe de mathématiciens français, que, d'après Liliane Alfonsi, spécialiste de Bézout, ce nom lui a été attribué. L'énoncé est plausible et tient en peu de mots : « On demande en combien de manières on peut payer 542 livres en donnant des pièces de 17 livres et recevant en échange des pièces de 11 livres. »

Cela revient, explique Bézout, en représentant par x le nombre des pièces de 17 livres et y celui des pièces de 11 livres, à résoudre en nombres entiers l'équation 17x – 11y = 542. L'auteur propose alors un véritable algorithme qui va, par une phase « descendante » puis une phase « montante », jusqu'au calcul de x et y : il extrait  

qu'il écrit :

 par division euclidienne. Comme  doit être entier (appelons u cet entier) : . Et on recommence : on extrait

dont le second terme est un entier t. Et on reprend :   d'où 

le second terme étant un entier s, on trouve t–3=5s ou t=5s+3. Fin de la première phase : on est sûr que t est entier !

Il s'agit maintenant d'entamer la seconde phase : remonter jusqu'à x et y. Facile ! On remplace t par 5s + 3 dans u, d'où u = 6s + 3, d'où le calcul de x = 11s + 6, pour finir par le calcul de y = 17s – 40 et conclure, comme Bézout, que l'on peut « satisfaire à cette question d'une infinité de manières différentes en mettant dans les valeurs de x et de y, au lieu de s, tous les nombres entiers positifs imaginables depuis 3 jusqu'à l'infini. »

Ainsi, les couples solutions de l'équation proposée sont (39, 11), (50, 28) … (94, 96), (105, 113), (116, 130) …

De là à résoudre en nombres entiers l'équation 17x – 11y =  1, il n'y a qu'un pas, que l'on franchit sur le même modèle pour trouver les couples (11s + 2, 17s + 3), soit (13, 20), (24, 37) … (57, 88) …, illustrant parfaitement le théorème de Bachet – Bézout avec a = 17 et b = –11 et suggérant une démarche pour sa démonstration, qui conduira à « l'heureuse » identité dans les cas où a et b ne sont pas forcément premiers entre eux.

Si cette « trouvaille » permet de résoudre la plus simple des équations diophantiennes, Bézout l'étendra aux polynômes et elle deviendra aussi une mine d'applications en théorie des nombres.