
Un outil oublié
 Dans un univers technologique où la moindre distance peut se déterminer de manière ultra-précise et quasi-instantanément, il est difficile d'imaginer qu'on a pu, à une époque, privilégier les constructions et les raisonnements sur des longueurs sans les mesurer. C'est de ces questions que traite la théorie des proportions dans laquelle s'intègre le théorème de Thalès.
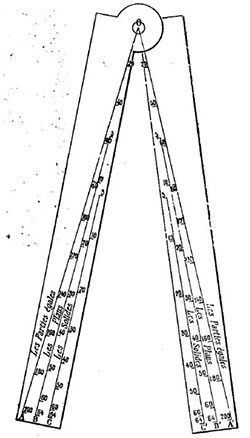
Dans un univers technologique où la moindre distance peut se déterminer de manière ultra-précise et quasi-instantanément, il est difficile d'imaginer qu'on a pu, à une époque, privilégier les constructions et les raisonnements sur des longueurs sans les mesurer. C'est de ces questions que traite la théorie des proportions dans laquelle s'intègre le théorème de Thalès.Parmi les instruments, qui, comme le quarré géométrique ou le bâton de Jacob (voir Mathématiques et Géographie, Bibliothèque Tangente 40, pages 79 et 81), font intervenir ce théorème dans leur conception ou dans leur utilisation, se trouve le compas de proportion. Généralement attribué à Guidalbo del Monte, il fait son apparition vers la fin du XVIe siècle. Il sera ensuite perfectionné par Galilée, qui lui consacre un ouvrage.
Diviser une longueur
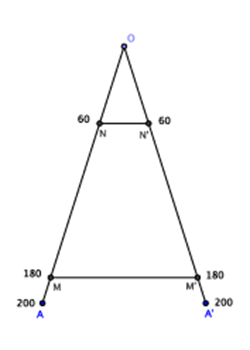 Les lignes des parties égales (ou lignes arithmétiques) OA et OA' d'un compas de proportion, graduées uniformément et de manière identique, permettent la division d'un segment en parties égales. Voici par exemple la procédure pour obtenir le tiers d'un segment donné à l'aide du compas de proportion : on ouvre le compas de telle sorte que la distance entre les graduations 180 (il faut choisir un multiple de 3) des deux branches soit exactement la longueur MM' du segment. La distance NN' entre les graduations 60 est alors exactement le tiers de la longueur MM'.
Les lignes des parties égales (ou lignes arithmétiques) OA et OA' d'un compas de proportion, graduées uniformément et de manière identique, permettent la division d'un segment en parties égales. Voici par exemple la procédure pour obtenir le tiers d'un segment donné à l'aide du compas de proportion : on ouvre le compas de telle sorte que la distance entre les graduations 180 (il faut choisir un multiple de 3) des deux branches soit exactement la longueur MM' du segment. La distance NN' entre les graduations 60 est alors exactement le tiers de la longueur MM'.
Dans un second exemple d'utilisation, on cherche à diviser notre segment en deux parties proportionnelles à 7 et 5 : le compas est ouvert pour faire coïncider la longueur MM' au niveau des graduations 120 (120 = 70 + 50) de chaque branche. On peut alors trouver la longueur de l'une des deux parties cherchées entre les graduations 70 ou entre les graduations 50.
Construire des figure semblables
Les lignes des plans (ou lignes géométriques) d'un compas de proportion, représentées par les segments [OB] et [OB'] sur la figure, permettent de déterminer le côté d'un triangle semblable d'aire proportionnelle à un triangle donné. Sur cette ligne, la graduation n correspond en fait à une distance OM de , où d est une unité choisie.

La graduation de la ligne des plans. Les distances réelles sont notées entre parenthèses. Ici, d = 8.
Supposons que l'on cherche à construire un triangle semblable d'aire trois cinquièmes d'un triangle donné. Le compas est ouvert pour faire coïncider la longueur MM' d'un côté du triangle d'origine avec la graduation 50 entre les deux branches. La longueur NN' récupérée entre les graduations 30 correspond alors à la longueur du côté correspondant du triangle cherché :
La ligne des plans permet également de déterminer une moyenne géométrique. On dispose de deux segments de longueurs respectives p et q et on sait que le rapport p / q vaut, par exemple, 17 / 53. On ouvre le compas de telle sorte que les graduations 53 coïncident avec le segment q. La distance NN' relevée au niveau des graduations 17 est alors la moyenne géométrique . En effet :
On en déduit :
Sur le même principe, les lignes des solides (ou lignes stéréométriques) OC et OC' sont utilisées pour déterminer le côté d'un tétraèdre de même forme mais de volume proportionnel à un tétraèdre connu. Sur cette ligne, le repère noté n correspond alors à une distance de (sur la représentation du compas de proportion, d = 4).
Lire la suite gratuitement