Le paradoxe de Thalès, c'est qu'il n'a laissé aucun écrit, mais que son œuvre a fait le tour du monde. A-t-il même écrit quelques-uns des résultats qu'on lui attribue ? Avait-il les éléments de logique nécessaires à l'établissement des raisonnements qu'on lui prête ? Les historiens attestent pourtant qu'il aurait rédigé un livre sur la navigation, où il décrit et utilise abondamment la constellation de la Petite Ourse, mais « on ne prête qu'aux riches » et tant de personnages importants se sont vu attribuer des résultats dans lesquels ils n'étaient pour rien ! Une chose est sûre cependant : Thalès était une figure prestigieuse de son temps, il a voyagé en Égypte et a rapporté en Grèce la science géométrique de ce pays. Quant aux résultats qu'il laisse à la postérité, mieux vaut les regarder avec circonspection.

Un homme de réputation

Il est difficile, concernant Thalès, de séparer la légende de l'histoire. On sait de lui qu'il naît vers 624 avant notre ère à Milet, en Asie mineure (aujourd'hui en Turquie) et qu'il meurt vers -547 dans la même ville, vraisemblablement de déshydratation en assistant à une compétition sportive. Tout à la fois commerçant enrichi, en particulier en spéculant sur le commerce des olives, conseiller militaire et ingénieur, c'est sa vie de premier philosophe grec, de savant et de mathématicien qui confère à Thalès de Milet tout son prestige.

Considérons de lui essentiellement ses activités scientifiques. Hérodote raconte qu'en -585 « soudain le jour s'est changé en nuit. L'événement avait été prévu par Thalès de Milet, qui en avait prévenu les Ioniens ». Certains, par contre, doutent que l'éclipse de soleil du 28 mai de cette année-là ait été prédite par Thalès, qui ne pouvait – disent-ils – pas connaître la période du cycle des éclipses solaires et aurait juste été là au bon moment pour qu'on lui attribue à lui, le savant reconnu, le mérite de la prédiction.

Il existe de même de nombreuses sources pour attester que Thalès avait mesuré la hauteur des pyramides : Diogène Laërce, au second siècle de notre ère, cite Hiéronyme de Rhodes, un élève d'Aristote affirmant « Thalès a réussi à mesurer la hauteur des pyramides en observant la longueur de leur ombre au moment où notre ombre est égale à notre propre hauteur », Pline le relate également. Plutarque raconte lui aussi l'histoire, laissant même entendre que Thalès avait déjà en tête l'idée des triangles semblables : « Sans aucun instrument, il a planté un bâton à l'extrémité de l'ombre de la pyramide et, ayant créé deux triangles par l'impact des rayons du soleil […] a montré que la pyramide avait au bâton le même rapport que l'ombre de la pyramide à l'ombre du bâton. » Bien sûr, Thalès a voyagé en Égypte, ses moyens le lui permettaient, mais pourquoi, s'interroge Paul Tannery, les Égyptiens, maîtres de Thalès, auraient-ils ignoré ce procédé élémentaire ? Une chose est sûre cependant, c'est qu'il savait utiliser des méthodes géométriques pour résoudre des problèmes concrets : il savait également, semble-t-il, déterminer la distance des vaisseaux en mer.

De la géométrie à la légende

Si l'on retrouve effectivement dans la mesure de la hauteur de la pyramide  la notion de triangles semblables, il semblerait que Thalès n'ait pas encore pu franchir le pas en conceptualisant celle de la similitude à partir d'un simple problème concret, ce que les géomètres grecs ont su faire, mais après Thalès.

Notre savant de Milet a cependant, toujours à partir de problèmes concrets, côtoyé des notions de géométrie plus étayées, mais apparaissant sous une forme plus diffuse. Il aurait fait des prouesses pour la mesure de distances inaccessibles. De nombreuses notions de géométrie gisent derrière ces problématiques. C'est pourquoi on va prêter à Thalès, dans bien des ouvrages historiques, des capacités mathématiques remarquables pour son temps, comme la découverte de cinq théorèmes de géométrie élémentaire (voir en encadré).

Ne prête-t-on pas un peu trop à Thalès ? Proclus, à propos du quatrième théorème de l'encadré, plutôt que de parler « d'angles égaux », parle « d'angles semblables », comme si Thalès n'avait aucun moyen ni de mesurer ni de comparer avec précision des angles et avait simplement affirmé que « les angles à la base d'un triangle isocèle ont l'air semblables ». Quant aux autres théorèmes, qu'est-ce qui permet de les attribuer à Thalès ? D'après Eudème, qui en donne une description détaillée et concrète, la méthode de Thalès pour mesurer les distances inaccessibles, traduite en termes d'aujourd'hui, pourrait se résumer à la figure ci-contre.

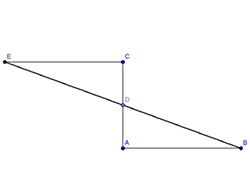La distance à mesurer est AB. L'observateur est placé en A. Il élève en ce point une perpendiculaire au terrain et repère sur cette droite deux points : C et D, le milieu de [AC]. Il vise depuis D le point B, retourne le viseur en gardant le même angle de visée pour le pointer en direction de la perpendiculaire en C à la verticale (AC), que le rayon de visée coupe en E. Et la distance CE est égale à la distance AB. Notons que le procédé nécessite quand-même que Thalès possède les concepts nécessaires pour le mettre en œuvre : est-ce si sûr ?

Le récit est toutefois cohérent, et l'on retrouve dans cette pratique au moins deux des théorèmes qu'Eudème attribue à Thalès : le deuxième, concernant les angles opposés par le sommet en D, et le troisième, où les triangles ABD et CED sont égaux, puisque les côtés AD et DC sont égaux, les angles en D (deuxième théorème) et en A et C (droits) aussi. Voilà déjà trois théorèmes retrouvés !

Le quatrième nous a été rapporté par l'historienne Pamphila, mais beaucoup plus tard, au I^er siècle de notre ère ; il prête donc un peu à caution. Elle raconte que « Thalès, qui avait appris la géométrie des Égyptiens, a été le premier à inscrire dans un cercle un triangle qui doit être rectangle, et il a pour cela sacrifié un bœuf ». D'autres, comme Apollodore, avaient attribué ce sacrifice à Pythagore ; cela prouve la confusion dans laquelle on navigue en parlant du mythique Thalès…